Условие задачи (1987, № 2) Задача М1026 // Квант. — 1987. — № 2. — Стр. 22; 1987. — № 6. — Стр. 21.
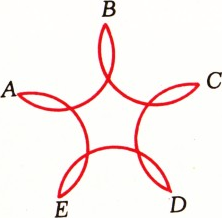
- Пять равных дуг
$AB$, $BC$, $CD$, $DE$, $EA$ расположены так, что каждая делится соседними на три равные части (рис. 1). Найдите величину каждой дуги (в градусах). - Тот же вопрос для «розетки» из
$m$ равных дуг, каждая из которых делится соседними на три равные части.
Изображения страниц
Решение задачи (1987, № 6) Задача М1026 // Квант. — 1987. — № 2. — Стр. 22; 1987. — № 6. — Стр. 21.
Решим задачу сразу в общем случае. Концы данных

