Задача М1‍‍

Ответ. Да, сможет.

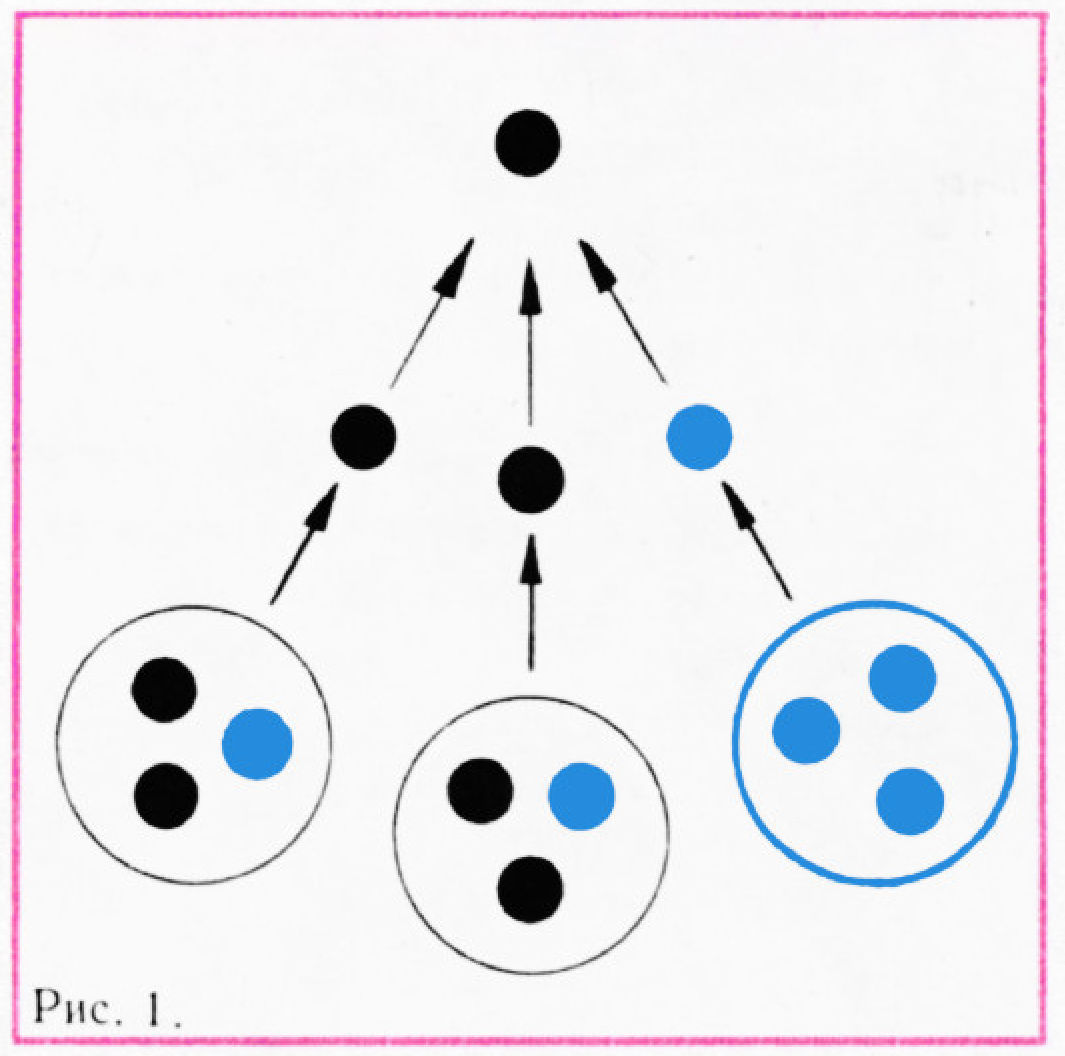
Прежде всего, разберёмся, как может на «многоступенчатых» выборах победить кандидат, за которого голосует меньшинство. (Кстати, по такой системе голосуют во многих капиталистических странах.) Самый простой пример такой ситуации изображён на рисунке 1: здесь девять избирателей — четыре «чёрных» и пять «голубых» — разбиты на три группы по три избирателя так, что в двух группах побеждают чёрные, и поэтому в результате таких «двухступенчатых выборов» будет избран кандидат чёрных, хотя число его сторонников составляет только $\dfrac{4}{5}$‍‍ от общего числа избирателей. (Нетрудно сообразить, что при двухступенчатых выборах с большим числом избирателей процент голосов, достаточный для победы, может быть ещё меньше, но всё-таки заведомо больше $25\%$‍.)‍ Ясно, что при трёхступенчатой системе выборов этот процент можно сделать ещё ниже. Например, если заменить на рисунке 1 каждого избирателя группой из ста человек, причём так, что в голубой группе все сто избирателей голубые, а в чёрной — 51 чёрный и 49 голубых, то мы получим пример ситуации, где черные составляют только $\dfrac49\cdot\dfrac{51}{100}=\dfrac{17}{75}$‍‍ от общего числа избирателей и тем не менее побеждают.

После этих предварительных соображений приведём решение задачи.

Разобьём всех избирателей на 5 групп по 4 миллиона в каждой так, что две группы целиком состоят из противников Мирафлореса (назовём эти группы «голубыми», а три остальные — «чёрными»). Каждую из этих групп «первого ранга» снова разобьём на 5 групп второго ранга, причём из пяти групп, составляющих черную группу первого ранга, три — чёрных и т. д., как указано в таблице.

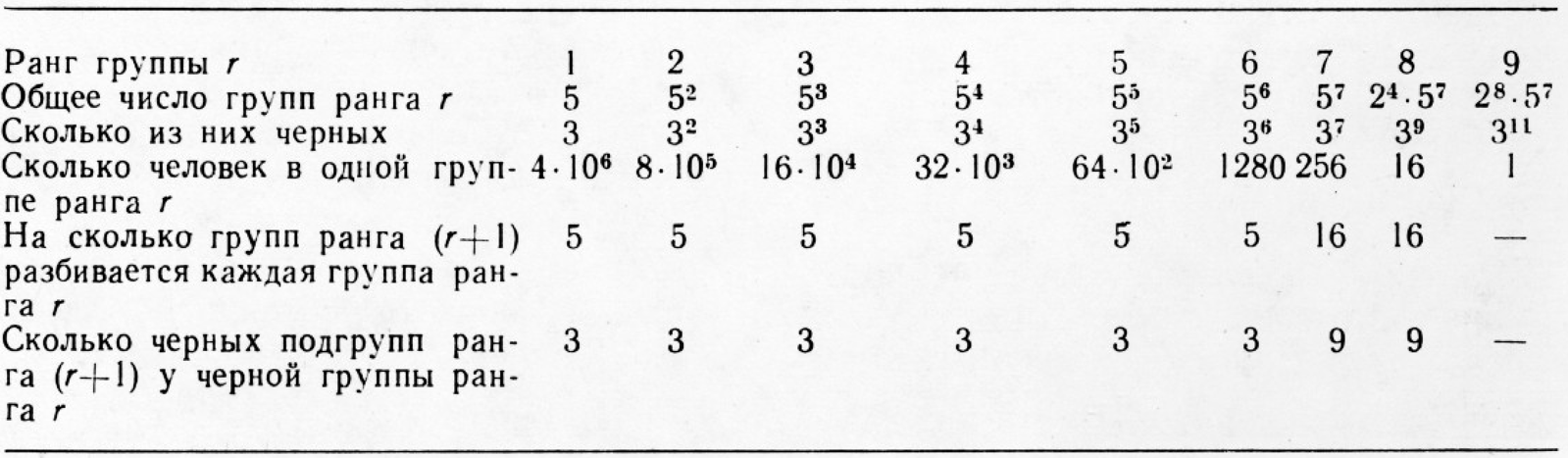
Ясно, что при таком разбиении для победы Мирафлореса достаточно, чтобы за него проголосовала $$ \dfrac{3^{11}}{2^8\cdot5^7}=\dfrac{177\,147}{20\,000\,000}\lt\dfrac1{100} $$ часть всех избирателей. Тем самым, поскольку армия составляет $\dfrac1{100}$‍‍ часть избирателей и поддерживает Мирафлореса, он сможет победить.

Некоторые читатели пытались решить следующий, более общий вопрос: какое наименьшее число сторонников должен иметь Мирафлорес, чтобы победить на «демократических выборах», если общее количество избирателей $N$‍?‍ Разумеется, ответ на этот вопрос зависит не столько от величины числа $N$‍,‍ сколько от того, как оно раскладывается на множители. Если, скажем, $N$‍‍ — число простое, то избирателей вообще никак нельзя разбить на равные группы (кроме тривиального способа: $N$‍‍ групп по одному человеку) и для победы нужно иметь простое большинство. Покажем, как ответить на этот вопрос для любого $N$‍.‍

Рассмотрим такое разбиение $N$‍‍ человек на группы (1-го, 2-го и т. д. ранга), при котором побеждает Мирафлорес и число его сторонников — наименьшее из возможных. Очевидно, можно считать, что в группах, голосующих против него, нет ни одного его сторонника и что все чёрные группы одного ранга разбиты совершенно одинаково. Удобно использовать обозначение $[~]$‍‍ — «целая часть» ($[x]$‍‍ — наибольшее целое число, не превосходящее $x$‍;‍ например, $[2] = 2$‍,‍ $\left[3\dfrac12\right]=3$‍).‍ Ясно, что если некоторая чёрная группа состоит из $k$‍‍ групп следующего ранга, то среди них должно быть не менее $[\dfrac k2+1]$‍‍ чёрных. Пусть каждая группа $r$‍‍-го ранга ($r=1$‍,‍ 2, $\ldots$‍,‍ $m-1$‍)‍ разбита на $k_r$‍‍ групп меньшего ранга, а группы последнего $m$‍‍-го ранга состоят из 1 человека. Тогда для победы чёрных необходимо иметь по крайней мере $$ B=\left(\left[\dfrac{k_1}2\right]+1\right) \left(\left[\dfrac{k_2}2\right]+1\right)\ldots \left(\left[\dfrac{k_m}2\right]+1\right) $$ чёрных голосов. Наша задача сводится к такой: разложить данное $N$‍‍ в произведение таких сомножителей $k_1$‍,‍ $k_2$‍,‍ $\ldots$‍,‍ $k_m$‍,‍ чтобы произведение $B$‍‍ было минимально.

Пусть $$ N = k_1 k_2 \ldots k_m\tag{*} $$ — такое разложение. Как показывает следующая лемма, можно предполагать, что в этом разложении нет сомножителей $k$‍‍ вида $k=pq$‍,‍ где $p$‍‍ и $q$‍‍ больше 2 (если такие есть, можно провести дальнейшее разложение, не увеличивая $B$‍).‍

Лемма.$$ \left(\left[\dfrac p2\right]+1\right)\left(\left[\dfrac q2\right]+1\right)\le \left[\dfrac{pq}2\right]+1 $$ для всех целых $p$‍‍ и $q$‍,‍ больших 2.

Доказательство. Если $p$‍‍ и $q$‍‍ оба чётны, то неравенство можно переписать так: $$ \begin{gather*} \left(\dfrac p2+1\right)\left(\dfrac q2+1\right)\le\dfrac{pq}{2}+1,\\ (p+2)(q+2)\le2pq+4,\\ pq-2q-2p+4\ge4,\\ (p-2)(q-2)\ge4, \end{gather*} $$ что, очевидно, верно для $p\gt2$‍‍ и $q\gt2$‍.‍

В случае, когда одно из чисел $p$‍,‍ $q$‍,‍ например $p$‍,‍ чётно, а другое нечётно, имеем: $$ \begin{gather*} \left(\dfrac p2+1\right)\left(\dfrac q2+1\right)\le\dfrac{pq}{2}+1,\\ (p+2)(q+1)\le2pq+4,\\ pq-2q-p+2\ge0,\\ (p-2)(q-1)\ge0. \end{gather*} $$

Случай, когда $p$‍‍ и $q$‍‍ нечётны, разбирается аналогично. Лемма доказана. Отсюда сразу следует, что нечётные $N$‍‍ надо раскладывать на простые множители «до конца». Осталось разобраться с двойками.

Можно считать, что в разложении нет сомножителей вида $2q$‍,‍ где $q$‍‍ нечётно, поскольку $$ 2\left(\left[\dfrac q2\right]+1\right)=\left[\dfrac{2q}{2}\right]+1. $$

Отсюда из леммы вытекает, что из чётных сомножителей можно ограничиться только двойками, четвёрками и восьмёрками. Далее ясно, что $2\cdot2$‍‍ хуже, чем 4, поскольку $\left(\left[\frac{2}{2}\right]+1\right)^2= 4\gt\left[\frac{4}{2}\right]+1=3$‍.‍ Выгодно $2\cdot4$‍‍ заменить на 8, поскольку $2\cdot3=6\gt5$‍;‍ $4\cdot4$‍‍ лучше, чем $2\cdot8$‍,‍ поскольку $3\cdot3=9$‍;‍ $2\cdot5=10$‍‍ и, наконец, $4\cdot4\cdot 4$‍‍ менее выгодно, чем $8\cdot8$‍,‍ поскольку $3\cdot3\cdot3=27$‍;‍ $5\cdot5=25$‍,‍ так что больше двух четвёрок оставлять нельзя.

Итак, окончательный ответ такой: пусть $N=2^dp_1\ldots p_m$‍,‍ где $m\ge0$‍,‍ $d\ge0$‍‍ — целые, $p_1$‍,‍ $\ldots$‍,‍ $p_m$‍‍ — нечётные простые числа. Обозначим произведение $$ \dfrac{p_1+1}2\ldots\dfrac{p_m+1}2 $$ через $P$‍.‍ Тогда наименьшее число сторонников Мирафлореса, достаточное для победы, равно $$ B=\left\{\colsep{0pt}{\begin{array}{rlr} 2P,&~\text{если}~d=1~&(\text{т. е.}~N=2p_1\ldots p_m);\\ 5^nP,&~\text{если}~d=3n~&(N=8^np_1\ldots p_m);\\ 3\cdot5^nP,&~\text{если}~d=3n+2~&(N=4\cdot8^np_1\ldots p_m);\\ 9\cdot5^nP,&~\text{если}~d=3n+4~&(N=4^2\cdot8^np_1\ldots p_m); \end{array}}\right. $$ здесь $n$‍‍ — целое число, $n\ge0$‍.‍

Этот ответ нашли ученик 9-го класса из Томска А. Гришков и (в другой форме) ещё несколько читателей. В частности, для $N=20\,000\,000=2^8\cdot5^7=4\cdot8^2\cdot5^7$‍‍ получаем $B=3\cdot5^2\cdot3^7=164\,025$‍.‍