Задача Ф65‍‍

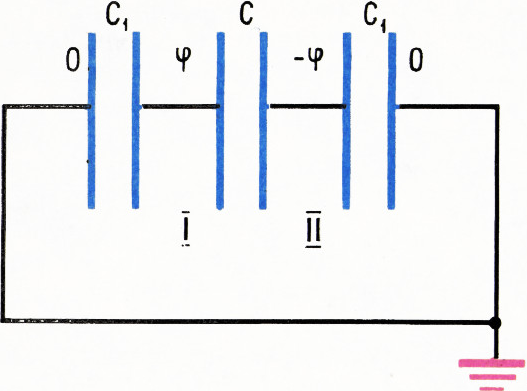
Нарисуем эквивалентную схему цепи (рис. 18). Так как разность потенциалов между пластинами конденсатора ёмкости $C$‍‍ равна $2\phi$‍,‍ то заряд каждой из пластин равен $$ q=C\cdot2\phi=2C\phi. $$

На пластинах же конденсаторов ёмкостью $C_1$‍‍ в этом случае находятся заряды $q_1=C_1\phi$‍.‍ Это означает, что заряд пластины II равен $$ Q=q+q_1=(2C+C_1)\phi. $$

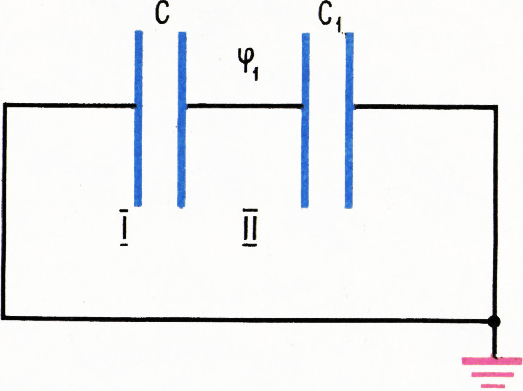
После того как пластина I будет заземлена, цепь станет такой, как показано на рисунке 19. При этом потенциалы пластин тоже изменятся. Обозначим потенциал пластины II через $\phi_1$‍.‍ На пластинах конденсатора ёмкости $C$‍‍ будет заряд $q'=C\phi_1$‍,‍ а нa пластинах конденсатора $C_1$‍‍ — заряд $q_1'=C_1\phi_1$‍.‍ Суммарный же заряд пластины II должен быть равен $Q$‍.‍ Поэтому $$ (2C+C_1)\phi=C_1\phi_1+C\phi_1. $$ Отсюда $$ \phi_1=\dfrac{2C+C_1}{C+C_1}\phi. $$

Так как напряжённость поля в конденсаторе равна $\dfrac{\Delta\phi}d$‍‍ ($\Delta\phi$‍‍ — разность потенциалов пластин и $d$‍‍ — расстояние между ними), то $$ \dfrac E{E_1}=\dfrac{2\phi}{\phi_1}=\dfrac{2(C+C_1)}{2C+C_1}. $$

Такое решение прислали А. Жуков из Кировска Донецкой области и Н. Федин из Омска.