Условие задачи (1970, № 8) Задача Ф47 // Квант. — 1970. — № 8. — Стр. 40; 1971. — № 4. — Стр. 42.
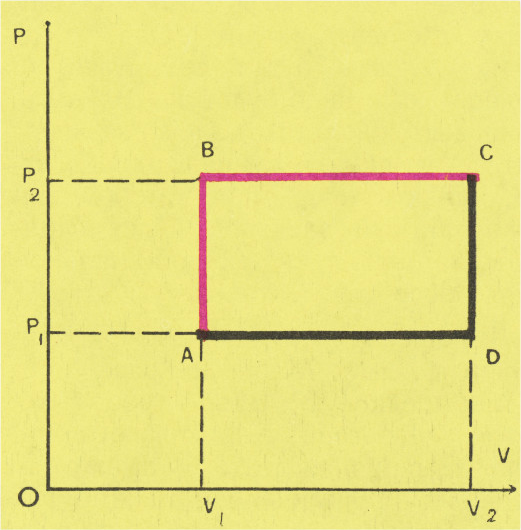
Если над идеальным газом совершается процесс
Изображения страниц
Решение задачи (1971, № 4) Задача Ф47 // Квант. — 1970. — № 8. — Стр. 40; 1971. — № 4. — Стр. 42.
Тепло, которое сообщается газу, идёт на увеличение его внутренней энергии
Из закона сохранения энергии следует, что $$
Q=W+P_2(V_2-V_1)
$$
и $$
Q_1=W+P_1(V_2-V_1),
$$
где
Из этих уравнений нетрудно найти, что $$ Q_1=Q-P_2(V_2-V_1)+P_1(V_2-V_1)=Q-(P_2-P_1)(V_2-V_1). $$
Величина
Разность
Правильное решение прислал А. Рогозин из Ижевска.

