Условие задачи (1970, № 1) Задача Ф3 // Квант. — 1970. — № 1. — Стр. 54; 1970. — № 7. — Стр. 57.
Из двух одинаковых кусков стальной проволоки свили две пружины. Диаметр витков одной из них равен
Изображения страниц
Решение задачи (1970, № 7) Задача Ф3 // Квант. — 1970. — № 1. — Стр. 54; 1970. — № 7. — Стр. 57.
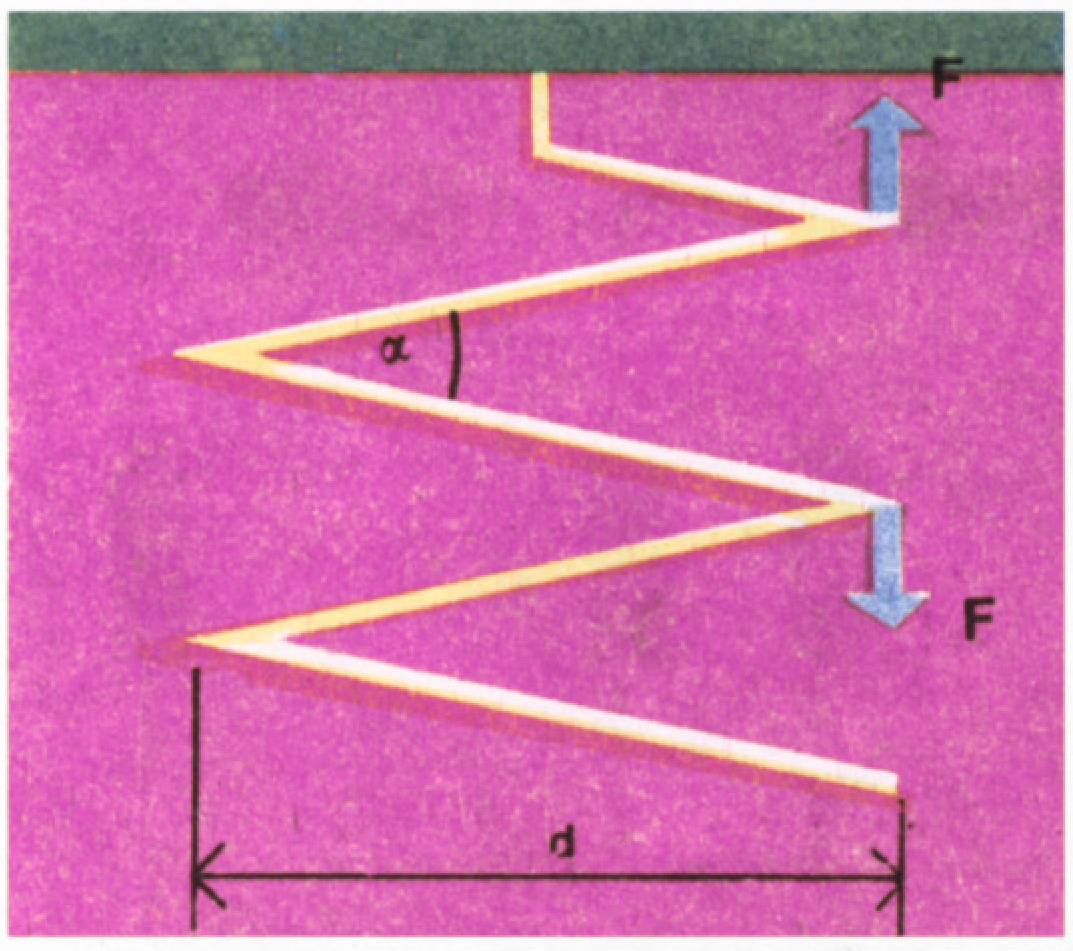
Удлинение пружины равно
Угол
Многие, приславшие решение этой задачи, правильно нашли, что удлинение
второй пружины в два раза больше, чем первой, но забыли, что вторая пружина
вдвое короче, чем первая, поэтому относительное удлинение второй пружины равно
не

