Условие задачи (1970, № 1) Задача Ф1 // Квант. — 1970. — № 1. — Стр. 53; 1970. — № 7. — Стр. 56.
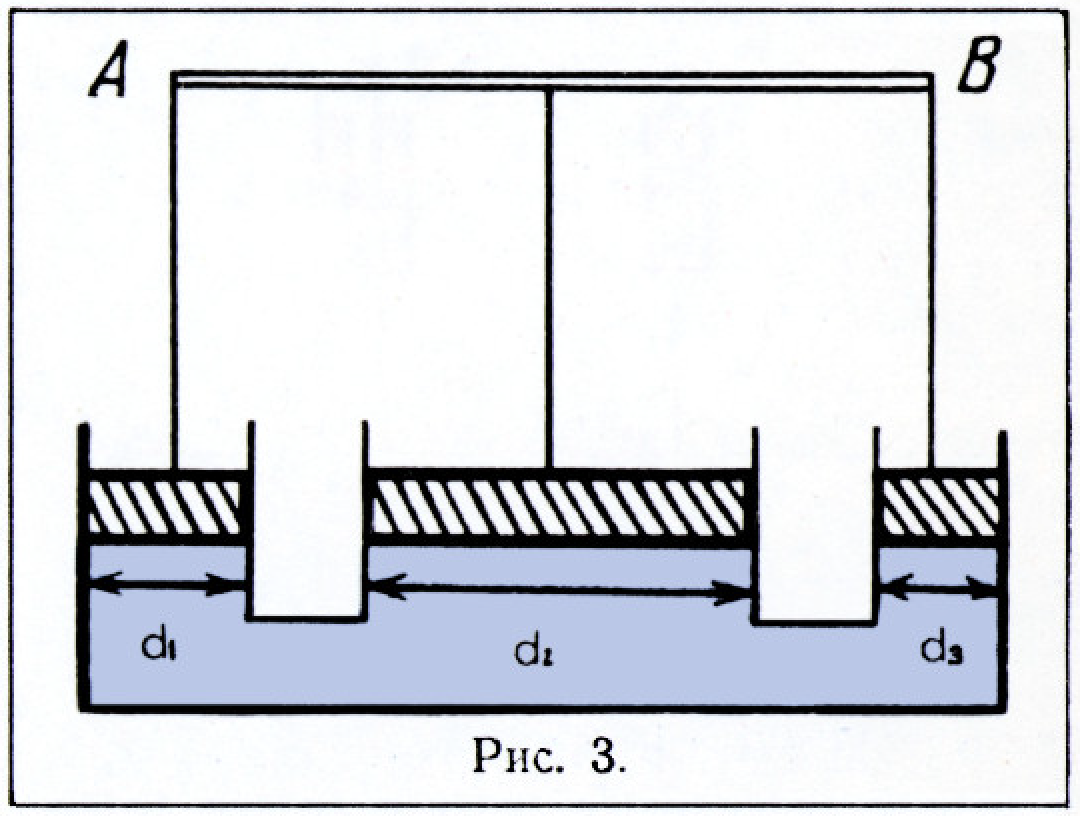
Три сообщающихся сосуда с водой, центры которых находятся на одинаковом расстоянии
Изображения страниц
Решение задачи (1970, № 7) Задача Ф1 // Квант. — 1970. — № 1. — Стр. 53; 1970. — № 7. — Стр. 56.
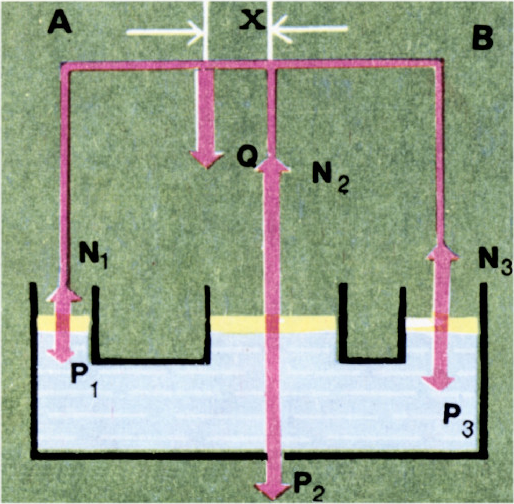
Стержень
Обозначив через
- равенство нулю суммы всех сил, действующих на стержень:
$F_1+F_2+F_3-Q=0$ и - равенство нулю суммы моментов всех сил, действующих на стержень,
относительно середины стержня:
$F_1a-F_3a-Qx=0$.
Подставляя в эти уравнения выражения для
Никто из читателей, приславших решение этой задачи, не учитывал масс поршней. Но только двое — Г. Кальшин из Кировобада и А. Карпенко из г. Лисицанска Ворошиловградской области — объяснили, почему это можно сделать. Так как поршни сделаны из одного и того же материала и имеют одинаковую толщину, то дополнительные давления на воду не зависят от диаметров поршней. Условие же равновесия поршней — это равенство давлений на воду во всех цилиндрах (так как уровни воды в цилиндрах одинаковы). Дополнительные давления из-за поршней этому условию удовлетворяют автоматически.

