Болотин А. С.

Математика игры «Сет»Болотин А. С. Математика игры «Сет» // Квант. — 2025. — № 8. — С. 2‍—‍6.‍‍

Карточная игра «Сет» была придумана в 1974 году Маршей Фалько, специалистом по популяционной генетике из Кембриджского университета. Она изучала дефекты зрения у коров, нарушения походки у лошадей, эпилепсию у немецких овчарок. Объясняя ветеринарам комбинаторные вопросы, возникающие в генетике, она использовала карточки со специальными символами. Впоследствии она поняла, что комбинирование этих карточек может лечь в основу игры. Так и появился «Сет».

Вначале рассмотрим саму игру «Сет» и несколько касающихся её элементарных комбинаторных вопросов, а после перейдём к обобщениям и связанным с игрой открытым вопросам математики.

Для игры «Сет» нужна колода карт. На каждой карте изображены одна, две или три одинаковые фигуры: ромбы, овалы или волны. Все фигуры на карте окрашены в синий, красный или зелёный цвет и могут иметь один из трёх типов заливки: сплошная, штрихованная и без заливки. На рисунке 1 изображены примеры карт из набора. Таким образом, у каждой карты есть четыре признака: количество фигур, форма фигур, цвет и заливка, каждый из которых может принимать три различных значения. Далее будем записывать признаки карты в виде $$ (\text{количество}{,}~\text{форма}{,}~\text{цвет}{,}~\text{заливка}). $$

В начале игры на стол выкладываются 12 карт. Задача заключается в поиске трёх карт, образующих сет. Сетом называется такой набор из трёх карт, что по каждому признаку они либо совпадают, либо полностью различаются. Например, карты $$ \colsep{0pt}{\begin{array}{llll} (1{,}&~\text{ромб}{,}&~\text{синий}{,} &~\text{сплошная}),\\ (2{,}&~\text{ромб}{,}&~\text{красный}{,}&~\text{сплошная}),\\ (3{,}&~\text{ромб}{,}&~\text{зелёный}{,}&~\text{сплошная}) \end{array}} $$ образуют сет, поскольку в первом и третьем признаках (количество и цвет) они полностью различаются, а во втором и четвёртом признаках (фигура, заливка) они совпадают. Когда игрок находит сет, он забирает соответствующие три карты себе, на стол вместо них выкладываются новые. Если игроки соглашаются, что среди выложенных карт нет сета, то на стол выкладываются ещё три карты из колоды. Игра продолжается до тех пор, пока не закончится колода и игроки не согласятся, что среди оставшихся на столе карт больше нет сета. Побеждает игрок, забравший наибольшее количество карт.

Первый естественный вопрос — сколько карт нужно для такой игры, если карты не повторяются? Также интересно посчитать, сколько всего комбинаций из трёх карт образуют сет. В следующих двух утверждениях содержатся ответы на эти вопросы, однако предварительно читателю предлагается самостоятельно подумать над ними.

Утверждение 1. В колоде содержится 81 карта.

Доказательство. У каждой карты есть 4 признака, каждый из которых может принимать 3 значения, поэтому всего карт $3^4=81$‍.‍

Утверждение 2. Существует 1080 комбинаций из 3 карт, образующих сет.

Доказательство. Рассмотрим произвольную пару карт. Заметим, что ровно одна карта образует в совокупности с данной парой сет. Рассмотрим произвольный признак. Если первые две карты совпадают по этому признаку, то и третья должна совпадать с ними по этому признаку. Например, если первые две карты красные, то и третья должна быть красной. Если же первые две карты различаются в этом признаке, то и третья должна отличаться от каждой из них по этому признаку. Например, если первая карта — красная, вторая — синяя, то третья обязана быть зелёной.

Таким образом, любая пара карт единственным образом продолжается до сета, и любой сет получается из трёх пар. Всего пар различных карт $C_{81}^2$‍,‍ значит, количество сетов равно $$ \dfrac{C_{81}^2}3=\dfrac{81\cdot80}{3\cdot2}=1080. $$ Заметим, что всего наборов из трёх различных карт $$ C_{81}^3=\dfrac{81\cdot80\cdot79}{3!}=85\,320. $$ Тогда доля сетов составляет $\dfrac{1080}{85\,320}=\dfrac1{79}\approx0{,}012658$‍,‍ т. е. лишь одна из семидесяти девяти троек карт образует сет.

Упражнение 1. Скажем, что сет имеет тип $(a,b)$‍,‍ если карты полностью различаются по $a$‍‍ признакам и полностью совпадают по $b$‍‍ признакам. Например, тройка (1, ромб, синий, сплошная), (1, ромб, красный, сплошная), (1, ромб, зелёный, сплошная) имеет тип $(1,3)$‍,‍ поскольку карты различаются лишь по цвету, но совпадают по остальным признакам. Сколько существует сетов каждого из возможных типов? Какую долю от всех сетов составляет каждый тип?

Обратим внимание на следующую деталь: правила игры предполагают, что среди 12 выложенных карт может не найтись ни одного сета. А сколько карт нужно выложить, чтобы хотя бы один сет был гарантированно?

Попробуем найти достаточно большое множество карт, среди которых нет сета. Рассмотрим набор карт, на которых либо 1, либо 2 фигуры, соответствующая фигура — либо ромб, либо овал, она покрашена либо в синий, либо в красный цвет, причём заливка либо сплошная, либо штрихованная. Таких карт всего $2^4=16$‍,‍ так как каждый из признаков может принимать только 2 значения. Заметим, что среди них нет трёх, образующих сет. Действительно, предположим, что какие-то три карты образовали сет. Рассмотрим первый признак, по принципу Дирихле у каких-то двух карт он совпадает, но тогда и третья карта совпадает с ними по этому признаку. Рассуждая аналогично для остальных признаков, получаем, что карты совпадают по всем признакам. Но это противоречит тому, что все карты различны. Значит, чтобы сет был, необходимо выложить хотя бы 17 карт. Однако всё ещё непонятно, достаточно ли 17 карт.

Упражнение 2. Проверьте, что выделенные жёлтым цветом карты на рисунке 2 образуют множество, в котором нет сета.

Приведённое упражнение показывает, что на самом деле необходимо выложить хотя бы 21 карту. Оказывается, это условие является и достаточным: среди 21 карты всегда есть три, образующие сет. Этот факт в 1971 году доказал итальянский математик Джузеппе Пеллегрино. Однако доказательство трудное, поэтому мы его здесь не приводим.

Заметьте, Пеллегрино доказал что-то про игру «Сет» ещё до того, как она была изобретена! Дело в том, что подобные вопросы возникали независимо в математике и раньше.

Итак, формализуем задачу математически. Закодируем каждое из значений каждого признака числами 0, 1, 2. Тогда каждую карту можно представить в виде вектора $\overrightarrow{x}=(x_1;x_2;x_3;x_4)$‍,‍ где $x_i$‍‍ принимают значения 0, 1, 2, при этом $x_1$‍,‍ кодирует количество, $x_2$‍‍ — фигуру, $x_3$‍‍ — цвет, $x_4$‍‍ — заливку. Теперь можно определить сложение карт. А именно, будем складывать покоординатно два вектора, соответствующие картам, по модулю 3: $$ (x_1;\ldots;x_4)+(y_1;\ldots;y_4)= (x_1+y_1~(\text{mod 3});\ldots;x_4+y_4~(\text{mod 3})). $$

Аналогично определяются вычитание карт и умножение карты на число.

Утверждение 3. Докажите, что карты $\overrightarrow{x}$‍,‍ $\overrightarrow{y}$‍,‍ $\overrightarrow{z}$‍‍ образуют сет тогда и только тогда, когда $\overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z}= (0;0;0;0)$‍.‍ Проверьте, что это условие эквивалентно каждому их следующих двух условий: $$ \overrightarrow{x}+\overrightarrow{z}=2\overrightarrow{y}\quad\text{и}\quad \overrightarrow{y}-\overrightarrow{x}=\overrightarrow{z}-\overrightarrow{y}. $$

Доказательство. Пусть $\overrightarrow{x}$‍,‍ $\overrightarrow{y}$‍,‍ $\overrightarrow{z}$‍‍ образуют сет. Рассмотрим первые координаты $x_1$‍,‍ $y_1$‍,‍ $z_1$‍.‍ Если они совпадают, то $$ x_1+y_1+z_1\equiv3x_1\equiv0~(\text{mod 3}). $$ Если они все различны, то $$ x_1+y_1+z_1\equiv0+1+2\equiv0~(\text{mod 3}). $$ Аналогично рассуждение для остальных координат, т. е. $\overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z}=(0;0;0;0)$‍.‍

Обратно, пусть $\overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z}= (0;0;0;0)$‍.‍ Рассмотрим первые координаты. Предположим, среди них есть совпадающие. Без ограничения общности будем считать, что $x_1=y_1$‍.‍ Тогда $$ z_1\equiv0-x_1-y_1\equiv-2x_1\equiv x_1~(\text{mod 3}), $$ т. е. все первые координаты векторов совпадают. Таким образом, либо первые координаты векторов совпадают, либо среди них нет двух одинаковых. Аналогично рассуждение для остальных координат. Но это условие и означает, что карты образуют сет.

Равносильность $$ \overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z}=(0;0;0;0) ~{\Leftrightarrow}~ \overrightarrow{x}+\overrightarrow{z}=2\overrightarrow{y} $$ следует из того, что $-1\equiv2~(\text{mod 3})$‍,‍ равносильность $$ \overrightarrow{x}+\overrightarrow{z}=2\overrightarrow{y} ~{\Leftrightarrow}~ \overrightarrow{y}-\overrightarrow{x}=\overrightarrow{z}-\overrightarrow{y} $$ очевидна. Утверждение доказано.

Заметим, что последнее условие означает, что $\overrightarrow{x}$‍,‍ $\overrightarrow{y}$‍,‍ $\overrightarrow{z}$‍‍ образуют арифметическую прогрессию.

Пользуясь только что доказанным утверждением, теперь можно легко решить следующее упражнение.

Упражнение 3. Во время игры игроки собрали 26 сетов. Докажите, что оставшиеся три карты также образуют сет.

Представим теперь, что карты имеют не 4 признака, а $n$‍,‍ где $n$‍‍ — какое-то натуральное число. Тогда карты можно представлять в виде векторов $\overrightarrow{x}=(x_1;x_2;\ldots;x_n)$‍,‍ где $x_i$‍‍ принимают значения 0, 1, 2. Дадим геометрическую интерпретацию для случая $n=2$‍‍ (случаи других $n$‍‍ можно рассмотреть аналогично). Отметим на плоскости 9 точек, у которых каждая координата принимает значения 0, 1, 2. Каждая карта, таким образом, соответствует точке на плоскости. Утверждение 3 говорит о том, что сеты в такой интерпретации — прямые, которые «идут по модулю 3» (рис. 3). Геометрическая интерпретация ещё поможет нам далее.

Обозначим через $r(n)$‍‍ размер наибольшего множества карт, среди которых нет сета. Так, выше мы уже поняли, что $r(4)=20$‍.‍ Также легко видеть, что $r(1)=2$‍,‍ $r(2)=4$‍‍ (проверьте!).

Упражнение 4. Докажите, что $r(n)\ge2^n$‍.‍

Упражнение 5. Докажите, что $r(3)\ge9$‍.‍

Используя геометрическую интерпретацию, докажем оценку $r(3)\le9$‍,‍ что в совокупности с упражнением 5 даст $r(3)=9$‍.‍

Утверждение 4. Для трёх признаков число карт, среди которых нет сета, не больше 9.

Доказательство. Аналогично двумерному случаю, рассмотрим 27 точек в трёхмерном пространстве с координатами 0, 1, 2 и предположим, что $r(3)\ge10$‍.‍ Тогда среди данных точек есть множество $M$‍‍ из 10 точек, никакие три из которых не лежат на одной прямой (т. е. не образуют сет). Заметим, что всё наше пространство можно разбить на 3  параллельные плоскости. Но поскольку $r(2)=4$‍,‍ то в каждой из этих плоскостей лежит не более 4 точек из $M$‍.‍ Тогда точки из $M$‍‍ на этих плоскостях могут быть распределены только в соответствии с разбиениями $10=4+4+2=4+3+3$‍.‍

Пусть $\alpha_0$‍‍ — та из этих плоскостей, на которой лежат 2 или 3 точки (скажем, $A$‍,‍ $B$‍‍ и, быть может, $C$‍).‍ Проведём через $A$‍‍ и $B$‍‍ прямую $l$‍.‍ Существует ровно три плоскости $\alpha_1$‍,‍ $\alpha_2$‍,‍ $\alpha_3$‍,‍ пересекающие $\alpha_0$‍‍ по $l$‍‍ (на рисунке 4 приведён пример расположения данных плоскостей и точек $A$‍‍ и $B$‍,‍ убедитесь, что общий случай аналогичен). Причём, вместе они покрывают все 27 точек.

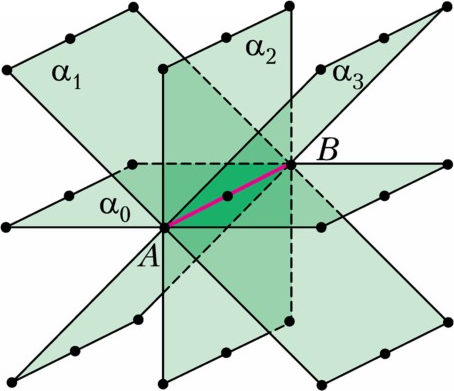
В силу того, что $r(2)=4$‍,‍ на каждой из плоскостей $\alpha_1$‍,‍ $\alpha_2$‍,‍ $\alpha_3$‍,‍ кроме $A$‍‍ и $B$‍,‍ лежит ещё не более 2 точек из $M$‍.‍ Осталось вспомнить, что на $\alpha_0$‍,‍ кроме $A$‍‍ и $B$‍,‍ лежит ещё не более 1 точки из $M$‍.‍ Таким образом, всего в $M$‍‍ не более $2+(1+2+2+2)=9$‍‍ точек, противоречие. Значит, $r(3)\le9$‍.‍ Утверждение доказано.

Итак, мы поняли, что $r(1)=2$‍,‍ $r(2)=4$‍,‍ $r(3)=9$‍,‍ $r(4)=20$‍.‍ На данный момент также известно, что $r(5)=45$‍,‍ $r(6)=112$‍.‍ Удивительно, но даже значение $r(7)$‍‍ до сих пор не вычислено! Вероятно, это связано с тем, что в основном интересуются поведением $r(n)$‍‍ при больших $n$‍.‍ А поскольку точно вычислить $r(n)$‍‍ трудно, то строят нижние и верхние оценки. На основании только что установленного равенства $r(3)=9$‍‍ получим оценку $r(n)$‍,‍ которая лучше приведённой в упражнении 4 при достаточно больших $n$‍.‍

Пусть $k=\left[\dfrac n3\right]$‍‍ — целая часть числа $\dfrac n3$‍,‍ $A=\{\overrightarrow{a_1};\ldots;\overrightarrow{a_9}\}$‍‍ — множество (построенное в упражнении 5) из 9 карт с 3 признаками, не содержащее сета. Рассмотрим теперь следующее множество карт с $n$‍‍ признаками: разобьём все признаки на блоки по 3 и в каждый блок поставим признаки из какого-то $\overrightarrow{a_i}$‍.‍ Последние $n-3k$‍‍ положим равными 0. Так, например, если $n=8$‍,‍ то построенное множество состоит из карт вида $$ (\overrightarrow{a_i},\overrightarrow{a_j},0,0). $$ Легко видеть, что в построенном множестве нет трёх карт, образующих сет, и в нём всего $9^n$‍‍ карт. Таким образом, $$ r(n)\ge9^k=9^{\left[\tfrac n3\right]}\ge9^{\tfrac n3-1}=\dfrac19(\sqrt[3]9)^n \approx\dfrac19\cdot2{,}08^n. $$

Нетрудно проверить, что при $n\ge56$‍‍ полученная оценка сильнее приведённой в упражнении 4. Так, при больших $n$‍‍ важным оказывается лишь множитель $(\sqrt[3]9)^n$‍‍ константа $\dfrac13$‍‍ не играет роли. Поэтому при получении оценок следят только за основанием степени.

Используя значения $r(4)$‍,‍ $r(5)$‍,‍ $r(6)$‍‍ и аналогичные рассуждения, можно улучшить полученную оценку.

Упражнение 6. На основании того, что $r(4)=20$‍,‍ получите для $r(n)$‍‍ нижнюю оценку порядка $(\sqrt[4]{20})^n\approx2{,}11^n$‍.‍

Лучшая известная нa данный момент нижняя оценка имеет порядок $2{,}2202^n$‍.‍ Помимо нижних оценок интерес представляют и верхние оценки. Как мы видели, нижние оценки имеют порядок $c^n$‍,‍ где $c$‍‍ — некоторая константа. Конечно, очевидная верхняя оценка $r(n)\le3^n$‍‍ (столько всего карт с $n$‍‍ признаками, каждый из которых принимает только три значения) имеет такой же вид. Однако в 1987 году была высказана гипотеза, что $r(n)\le c^n$‍,‍ где $c\lt3$‍.‍ Выдающийся математик Теренс Tao называл эту гипотезу своей любимой открытой задачей. Одна из первых полученных верхних оценок выглядела так: $$ r(n)\le\dfrac{2\cdot3^n}n. $$

Убедитесь, что такая оценка хуже, чем $c^n$‍,‍ где $c\le3$‍.‍ Эта оценка несколько раз улучшалась, но лишь в 2016 году упомянутая гипотеза была полностью доказана. Лучшая известная на данный момент верхняя оценка имеет порядок $2{,}756^n$‍.‍ Вопрос о точном поведении $r(n)$‍‍ до сих пор остаётся открытым.

Рассмотренная нами задача является классической в аддитивной комбинаторике (от англ. addition — сложение). Неформально аддитивная комбинаторика занимается поиском связей между комбинаторной структурой и аддитивной структурой, иногда в этот ряд добавляется мультипликативная структура (от англ. multiplication — умножение). Данные понятия не являются строгими, но чтобы понять, о чём идёт речь, рассмотрим пример.

Множество натуральных чисел определяется «аддитивно»: первый его элемент равен 1, каждый следующий получается из предыдущего прибавлением 1. С другой стороны, в силу основной теоремы арифметики каждое натуральное число, большее единицы, можно единственным образом разложить в произведение простых. Таким образом, в каком-то смысле простые числа формируют мультипликативную структуру натуральных чисел, а величина каждого числа (количество прибавлений единицы) — аддитивную структуру. При смешивании аддитивной и мультипликативной структур зачастую получаются сложные задачи, над которыми на протяжении многих лет думают математики. Например, возникают следующие вопросы.

• Аддитивные вопросы о мультипликативной структуре:
  • Как ведёт себя величина $n$‍‍-го простого числа $p_n$‍?‍
  • Что можно сказать про разность $p_{n+1}-p_n$‍‍ между соседними простыми?

Первый вопрос связан с теоремой о распределении простых чисел и гипотезой Римана — одной из немногих нерешённых проблем Гильберта. Относительно второго вопроса лишь в 2013 году было доказано существование некоторой константы $C$‍‍ такой, что для бесконечного количества пар $p_{n+1}-p_n\le C$‍.‍ Позднее было показано, что $C$‍‍ можно взять равным 246. Известная гипотеза о простых близнецах говорит, что подойдёт и $C=2$‍.‍

• Мультипликативные вопросы об аддитивной структуре:
  • Как разложить число $n$‍‍ на простые множители?
  • Как связаны разложения на простые множители чисел $n$‍‍ и $n+1$‍?‍

Первый вопрос связан с теорией алгоритмов. На данный момент не известно ни одного «достаточно быстрого» алгоритма разложения числа на простые множители. Однако существует тест Агравала Каяла Саксены, позволяющий «достаточно быстро» проверить, является ли число простым, а также «достаточно быстрый» квантовый (требующий вычислений на квантовом компьютере) алгоритм Шора разложения числа на простые множители. Второй вопрос оказывается связан с гипотезой Коллатца, о которой Эрдёш говорил, что математики пока не готовы к таким задачам.

Игра «Сет» возникает как комбинаторный объект — мы рассмотрели карточки, у которых есть некоторые признаки, принимающие разные значения. Однако утверждение 3 показало, что вопросы о формировании сета можно задавать в терминах аддитивной структуры. С другой стороны, мы увидели и чисто геометрическую интерпретацию, где сеты суть прямые в некотором пространстве.

Такая интересная и разная математика может скрываться за простой детской игрой!