Изображения страниц
Текст статьи Кохась К. П. 71 узелок // Квант. — 2024. — № 11/12. — С. 34—36.
— Разумеется, произведения иску-у-усства не стареют, — объяснял коллега Спрудль. — Но я не люблю бессмысленные финтифлюшки. Хочется, чтобы антикварная ве-е-ещь была бы функциональной, чтобы она была не просто древней, но при этом и — бульк — как бы это сказать, высокотехнологичной в своём классе.
— Понимаю, — сказал Горгулий. — Думаю, я смогу вам помочь. Вы знаете, что такое египетский треугольник?
— Пе-е-ервый раз слышу, бульк!
— Совершенно гениальный инструмент, хотя и кажется немного простоватым. Использовался при строительстве египетских пирамид!
— Что вы говорите, — заинтересовался коллега Спрудль.
— Это верёвка, связанная в кольцо, на которой завязано 12 узелков. С её помощью отмерялись прямые углы. Это потрясающе! Чтобы отмерить прямой угол, вы берёте первый, четвёртый и восьмой узелки и тянете их в стороны, чтобы получился треугольник. Тогда угол, в вершине которого находится четвёртый узелок, — прямой!
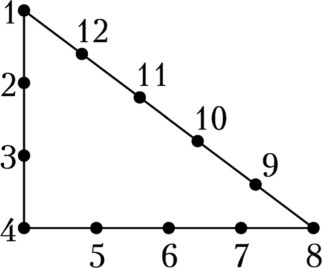
— Любопытно, любопытно, — пробормотал коллега Спрудль, разглядывая чертёж (рис. 1).
— Но мало кто знает, — продолжал Горгулий, — что имеется куда более продвинутый вариант этого инструмента. Это... древнешумерский треугольник!
Горгулий достал из ящика стола красивую, довольно потёртую верёвку, на которой было завязано очень много узелков.
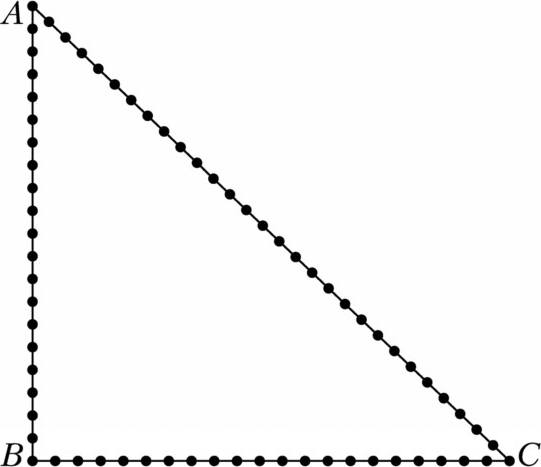
— От древних шумеров мало что осталось, — с нотками сожаления произнёс
Горгулий. — Истинные шедевры слишком хрупки. Это всего лишь более поздняя
имитация. Но время не в силах стереть интеллектуальную ауру этого предмета!
Смотрите, здесь не 12 узелков, а существенно больше — 71. В то время ещё не додумались до идеи завязать эту верёвку в кольцо. Для построения прямого
угла
— Беру! — клюнул, наконец, коллега Спрудль.
— Следующий год — год Пифагора, — сказала Огрыза, заходя в комнату. — Смотрите, какой замечательный новогодний флажок я купила у коллеги Спрудля. Очень красиво, да и недорого!
— Я тоже купил у него флажок, — сказал дятел Спятел.
— И я, — поддакнула Бусенька.
— Вы, кажется, очень довольны своими покупками, — сказал таракан Кузька. — Неужели коллега Спрудль стал положительным персонажем?
— Вряд ли, — с сомнением сказала Огрыза, — но ему единственному пришла в голову очень удачная идея делать и продавать новогодние флажки в форме прямоугольного треугольника.
— При чём тут прямоугольные треугольники? Что тут удачного? — не понял Кузька.
— Ну как же, с именем Пифагора связана знаменитая теорема, — объяснил
дятел Спятел. — В любом прямоугольном треугольнике с катетами
— Не может быть! — воскликнул Кузька. — В любом прямоугольном треугольнике?
— В любом! — подтвердил дятел Спятел.
— Я должен это проверить! Дайте мне ваши флажки! — сказал Кузька и убежал за рулеткой.
Бусенька, дятел Спятел и Огрыза положили на стол свои флажки, и Кузька принялся за измерения, бегая с рулеткой от одного флажка к другому. Время от времени он откладывал рулетку и кружился на одном месте, словно танцевал.
— Всё-таки это завораживающее зрелище, когда Кузька что-то вычисляет, — похвалила Бусенька. — Эти его приёмы счёта на лапах порою выглядят как настоящий балет.
— Готово! — доложил Кузька, — я всё проверил. Диагноз ясен: вы слишком увлекаетесь авторитетами. Теорема Пифагора неверна!
— Как неверна? Почему неверна? — хором спросили Бусенька и дятел Спятел.
— Кажется, кто-то из нас спятил, — предположила Огрыза.
— Я очень аккуратно вычислил стороны ваших флажков в миллиметрах и для каждого из них подсчитал величину
Все с удивлением смотрели на Кузьку.
— Забавно, — сказал, наконец, дятел Спятел. — Я заплатил за свой флажок как раз 3 рубля 17 копеек.
— A я за свой 2 рубля 65 копеек, — сказала Огрыза.
— А я за свой, — театрально закатив глаза, медленно произнесла Бусенька, — 2 рубля 20 копеек!
Теперь уже Кузька смотрел на остальных, как на новые ворота.
— Мистика какая-то, — сказал он.
— По крайней мере, из твоих вычислений ясно, что наши флажки — это не прямоугольные треугольники, — сказала Бусенька. — Угол, который мы считали
прямым, на самом деле чуть-чуть больше
— По площади, — сказала Огрыза. — Он при мне измерил катеты флажка, перемножил их, поделил на 2 и сообщил: «Площадь флажка столько-то квадратных сантиметров», а потом вычислил цену флажка, умножив площадь на цену одного квадратного сантиметра.
— Но ведь флажок непрямоугольный, — возмутился дятел Спятел, — его площадь меньше половины произведения сторон! Значит, он завысил площадь, а вместе с ней и цену!
— Может, он ошибается, потому что думает, что флажки у него прямоугольные, — предположила Бусенька. — А то, что все его ошибки в его пользу, — это рефлекс, который он вырабатывал годами. Как он выкраивает флажки? С помощью угольника?
— Ааааа... Кажется, я знаю как! — догадался дятел Спятел. — С помощью египетского треугольника! Точнее, не египетского, а древнешумерского!
— Древне... какого? — не понял Кузька.
— Древнешумерского! Горгулий завязал на старой верёвке 71 узелок и продал её коллеге Спрудлю по цене антиквариата. Будто бы это древний инструмент для построения прямых углов. Узелки завязаны через равные расстояния. Совмещая первый узел с последним, мы строим с помощью верёвки треугольник со сторонами 20, 21 и 29.
—
— Очень древний, — подтвердила Бусенька, — и довольно-таки шумерский. Вот только мне кажется, что очень неудобно всё время совмещать первый и последний узел. Почему бы не связать концы верёвки в том месте, где совмещаются узлы?
— Действительно неудобно, — согласилась Огрыза. — Видимо, коллега Спрудль так и сделал. Но если при этом он совместил крайние узлы, то у него получился двойной или даже тройной узел — очень неуклюжая конструкция.
— Я думаю, он не стал бы завязывать лишний узел, — сказал дятел Спятел. — Ведь это была бы очевидная подделка, уменьшающая историческую ценность инструмента. Наверно, он завязал незаметный узелок, а то и вовсе склеил концы верёвки.
— Если предположить, что он удлинил при этом верёвку на одно звено, —
подытожила Бусенька, — то получится, что для откладывания прямого угла он строит треугольник
— Подумать только, лишние 4 градуса, — сказал дятел Спятел, внимательно рассматривая свой флажок.
— Но как же так получилось, — спросил Кузька, — что цена флажка равна
величине
— У наших флажков углы
— Не может быть! — не поверил Кузька.
Вопросы
- Вооружившись калькулятором, найдите, сколько стоит один квадратный сантиметр флажка у коллеги Спрудля.
- Большую ли прибыль получал коллега Спрудль из-за неправильного подсчёта площади, иными словами, на сколько процентов он завышал площадь флажка?
Ответы, указания, решения
- Так как в сантиметрах и копейках
$x\cdot\dfrac12ab=c^2-a^2-b^2$, то $$ x=4\cdot\dfrac{c^2-a^2-b^2}{2ab}=-4\cos\gamma\approx0{,}281~\text{коп/см}^2. $$ - Вместо величины
$\dfrac12ab\sin\gamma$ коллега Спрудль использовал величину$\dfrac12ab$, которая в$\dfrac1{\sin\gamma}\approx1{,}0025$ раз больше. Таким образом, его прибыль составляла около$\dfrac14$ процента.


