Козлов В. В.

Соударение телКозлов В. В. Соударение тел // Квант. — 1988. — № 9. — С. 30‍—‍36.‍‍

Некоторые физические теории построены по образцу, принятому в математике, — из небольшого числа физических утверждений, которые играют ту же роль, что аксиомы в математических теориях, логически строго выводятся разнообразные следствия. Эта статья посвящена одной такой теории — теории соударения тел. Явление удара хорошо описывается несложной математической моделью. Неудивительно поэтому, что законы удара были установлены до открытия основных принципов динамики.

Ещё Галилей поставил ряд опытов для выяснения законов соударения тел. Эти опыты, правда, не привели его к определённым выводам. Современник Галилея, пражский профессор Марци в своём сочинении «De proportione motus» (1639) опубликовал некоторые результаты своих исследований явления удара. В частности, ему было известно, что тело, упруго ударившись о такое же покоящееся тело, теряет свою скорость, сообщая её этому телу. Первое детальное исследование законов удара было предпринято в 1668 году по предложению Лондонского королевского общества. Три выдающихся механика и математика Валлис, Рен и Гюйгенс представили свои работы, в которых они изложили законы движения соударяющихся тел. Джон Валлис ограничился, не оговаривая этого, рассмотрением абсолютно неупругого удара. Он исходил из гипотезы о сохранении суммарного импульса сталкивающихся тел. Кристофер Рен изложил правила расчёта упругого удара. Рен, как и Валлис, не привёл никаких теоретических рассмотрений, однако для проверки своих правил он проделал ряд простых и убедительных опытов. На эти опыты ссылался Ньютон в своих знаменитых «Математических началах натуральной философии» (1687). Конкурсный мемуар Христиана Гюйгенса был наиболее полным исследованием по теории удара. В нём был намечен вывод соотношений теории удара, основанный на принципе относительности Галилея. Лондонское королевское общество напечатало лишь мемуары Валлиса и Рена. Гюйгенс напечатал свой мемуар в 1669 году в парижском «Журнале учёных».

Сохранение импульса

Рассмотрим ряд задач механики, связанных с исследованием соударения двух тел с массами $m_1$‍‍ и $m_2$‍,‍ движущихся по прямой без воздействия каких-либо сил. Пусть $v_1$‍‍ и $v_2$‍‍ — скорости этих тел до удара (рис. 1). Мы будем считать скорость алгебраической величиной: если тело движется вправо, то его скорость положительна, а если влево, то отрицательна. В момент удара на тела действуют только внутренние силы; поэтому их суммарный импульс $m_1v_1+m_2v_2$‍‍ сохраняется. Пусть $v_1'$‍‍ и $v_2'$‍‍ — скорости тел после удара. Из сохранения суммарного импульса получаем соотношение $$ m_1v_1+m_2v_2=m_1v_1'+m_2v_2'.\tag1 $$

Из одного этого уравнения, конечно, нельзя найти $v_1'$‍‍ и $v_2$‍.‍ Это и неудивительно: соударения бывают разными. Есть упругие и неупругие. Например, при абсолютно неупругом ударе тела слипаются и движутся затем как одно целое. В этом случае $v_1'=v_2'=v$‍‍ и из формулы (1) находим скорость слипшихся тел после удара: $$ v=\dfrac{m_1v_1+m_2v_2}{m_1+m_2}.\tag2 $$

Задача 1. Пусть $v_1\le v_2$‍.‍ Докажите, что $v_1\le v\le v_2$‍.‍

Изменение кинетической энергии

Кроме импульса в механике важную роль играет кинетическая энергия, равная $\dfrac{mv^2}2$‍,‍ где $m$‍‍ — масса тела, $v$‍‍ — его скорость. Рассмотрим абсолютно неупругий удар двух тел. В этом случае $$ \Delta T=\left(\dfrac{m_1v_1^2}2+\dfrac{m_1v_1^2}2\right)- \dfrac{(m_1+m_2)v^2}2 $$ называется потерянной кинетической энергией.

Следующее утверждение называется первой теоремой Карно:

Потерянная кинетическая энергия равна энергии точки массой $\mu=\dfrac1{\dfrac1{m_1}+\dfrac1{m_2}}$‍,‍ которая движется со скоростью, равной разности скоростей точек до удара: $$ \Delta T=\dfrac{\mu(v_1-v_2)^2}2. $$

Задача 2. Докажите первую теорему Карно.

Масса $\mu$‍‍ называется в механике приведённой массой системы. Она равна половине среднего гармонического чисел $m_1$‍‍ и $m_2$‍.‍

Задача 3. Докажите неравенства $$ \mu\le\dfrac{m_1+m_2}4,\quad\mu\le\dfrac12\sqrt{m_1m_2}. $$

Введём в рассмотрение потерянные скорости: $u_1=v-v_1$‍,‍ $u_2=v-v_2$‍,‍ с помощью которых формулируется вторая теорема Карно:

Потерянная кинетическая энергия равна суммарной кинетической энергии тел с массами $m_1$‍‍ и $m_2$‍,‍ движущихся с потерянными скоростями $u_1$‍‍ и $u_2$‍‍: $$ \Delta T=\dfrac{m_1u_1^2}2+\dfrac{m_2u_2^2}2. $$

Задача 4. Докажите вторую теорему Карно.

---

Галилео Галилей (1564‍—‍1642) — итальянский физик, математик и астроном. В главном сочинении Галилея по математике и физике, написанном в форме диалогов, заложены основы механики: установлены законы статики, равномерного движения, падения тел и колебания маятника. Инквизиция преследовала Галилея за книгу, написанную в поддержку гелиоцентрической системы.

Йоханнес Маркус Марци (1595‍—‍1667) — чешский философ, математик, физик, врач, профессор медицины и ректор Пражского университета. Марци развивал экспериментальный метод исследования. Он выяснил, как зависит продолжительность колебания маятника от его длины, и предложил использовать колебания маятника для измерения пульса пациентов.

Джон Валлис (1616‍—‍1703) — английский математик и механик, член-основатель Лондонского королевского общества, один из пионеров анализа бесконечно малых. Получил формулу, выражающую число $\pi$‍‍ в виде бесконечного произведения: $$\dfrac\pi2=\dfrac{2\cdot2\cdot4\cdot4\cdot6\cdot6\cdot\ldots} {1\cdot3\cdot3\cdot5\cdot5\cdot7\cdot\ldots}.$$ Считал арифметику основой математики.

Христиан Гюйгенс (1629‍—‍1695) — голландский механик, физик и математик. Первый президент французской Академии наук, был первым иностранным членом Лондонского королевского общества. Гюйгенс — непревзойдённый часовой мастер. Он изобрёл часы с маятником (ходики) и карманные часы с балансиром.

Кристофер Рен (1632‍—‍1723) — английский математик, механик и архитектор, член-основатель Лондонского королевского общества. Рен возглавил строительные работы в Лондоне после грандиозного пожара 1666 года. Его главное достижение в архитектуре — собор св. Павла.

Лазар Карно (1753‍—‍1823) — генерал, военный министр французской республики, игравший важную роль во время революции. В народе его называли «организатором побед». Результаты своих исследований по теории удара он изложил в 1783 году в анонимно изданной книге «Опыт о машинах вообще некоего офицера инженерных войск».

---

Рассмотрим теперь противоположный случай: абсолютно упругий удар. По определению, в этом случае, кроме суммарного импульса, сохраняется ещё суммарная кинетическая энергия: $$ m_1v_1^2+m_2v_2^2=m_1(v_1')^2+m_2(v_2')^2. $$

Задача 5. Докажите, что в случае абсолютно упругого удара относительные скорости тел до и после удара равны по величине и противоположны по направлению: $$ v_1-v_2=-(v_1'-v_2').\tag3 $$

Задача 6. Докажите равенства: $$ \begin{aligned} v_1'&=\dfrac{m_1-m_2}{m_1+m_2}v_1+\dfrac{2m_2}{m_1+m_2}v_2,\\[9pt] v_2'&=\dfrac{2m_1}{m_1+m_2}v_1+\dfrac{m_2-m_1}{m_1+m_2}v_2. \end{aligned}\tag4 $$

В частном случае, когда $m_1=m_2$‍,‍ эти формулы приобретают наиболее простой вид: $$ v_1'=v_2,\quad v_2'=v_1. $$ Следовательно в момент абсолютно упругого удара происходит обмен скоростями. Как уже говорилось, этот эффект был впервые описан Марци.

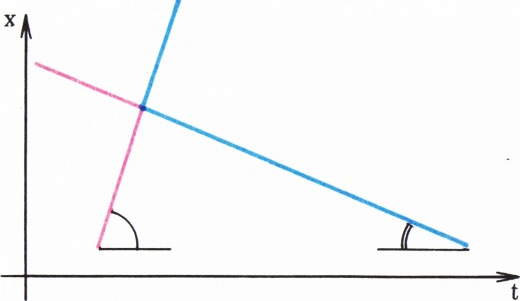
Абсолютно упругий удар тел равной массы удобно изображать на графиках движения тел, т. е. на графиках зависимости координат от времени (рис. 2). Эта графическая интерпретация используется в следующей задаче.

Задача 7. По прямой движутся с постоянными (не обязательно равными) скоростями несколько одинаковых шариков. Предположим, что соударения между ними абсолютно упругие и в каждом соударении участвуют только два шарика. Докажите, что общее число соударений конечно.

Рассмотрим ещё один частный случай, когда масса $m_1$‍‍ много меньше массы $m_2$‍.‍ Тогда $$ \begin{aligned} \dfrac{m_1-m_2}{m_1+m_2}&=\dfrac{\dfrac{m_1}{m_2}-1}{\dfrac{m_1}{m_2}+1} \approx-1,\\[18pt] \dfrac{2m_1}{m_1+m_2}&=\dfrac{2\dfrac{m_1}{m_2}}{\dfrac{m_1}{m_2}+1} \approx0,\\[18pt] \dfrac{2m_2}{m_1+m_2}&=\dfrac{2}{\dfrac{m_1}{m_2}+1}\approx2, \end{aligned} $$ так как отношение масс $\dfrac{m_1}{m_2}$‍‍ близко к нулю. С учётом этих замечаний формулы (4) примут следующий вид: $$ v_1'=-v_1+2v2=v_2-(v_1-v_2),\quad v_2'=v_2.\tag5 $$ Следовательно, второе тело не изменит своей скорости, а первое будет двигаться за вторым, отставая от него со скоростью, равной их относительной скорости до удара.

На практике, однако, чаще встречаются случаи, когда в момент удара тела не слипаются, но и их суммарная энергия не сохраняется. В этой ситуации обычно принимают гипотезу Ньютона, заменяя соотношение (3) следующим соотношением: $$ e(v_1-v_2)=-(v_1'-v_2'). $$ Здесь $e$‍‍ — некоторый безразмерный коэффициент, заключённый в промежутке от 0 до 1 и определяемый обычно из эксперимента. Число $e$‍‍ называют коэффициентом восстановления. При $e=0$‍‍ получается абсолютно неупругий удар, а при $e=1$‍‍ удар будет абсолютно упругим.

Пусть $u_1$‍‍ и $u_2$‍‍ снова обозначают потерянные скорости.

Величина потерянной энергии в общем случае вычисляется с помощью обобщённой теоремы Карно: $$ \Delta T=\dfrac{1-e}{1+e}\left(\dfrac{m_1u_1^2}2+\dfrac{m_2u_2^2}2\right). $$ При $e=0$‍‍ это утверждение известно нам как вторая теорема Карно; при $e=1$‍‍ потери энергии вообще не происходит — удар абсолютно упругий.

Задача 8. Докажите обобщённую теорему Карно.

Адиабатический инвариант

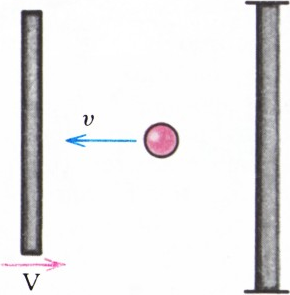
В качестве поучительного применения формул (5) рассмотрим следующую задачу. Шарик движется между двумя стенками, одна из которых неподвижна, а другая приближается к ней со скоростью $V$‍‍ (рис. 3; шарик начинает движение от неподвижной стенки). Удар шарика о стенки абсолютно упругий. После столкновения с неподвижной стенкой величина скорости шарика не меняется, а после каждого столкновения с подвижной стенкой скорость шарика (см. формулы (5)) увеличивается на $2V$‍.‍ Следовательно, энергия шарика тоже увеличивается. Пусть $v_0$‍‍ — величина скорости шарика в начальный момент времени (т. е. момент «нулевого» удара о неподвижную стенку), $l_0$‍‍ — расстояние между стенками в этот момент. Аналогично, через $v_n$‍‍ и $l_n$‍‍ обозначим величину скорости шарика и расстояние между стенками в момент $n$‍‍-го удара шарика о неподвижную стенку. Положим $I_n=v_nl_n$‍‍ ($n=0$‍,‍ 1, 2, $\ldots$‍).‍

Задача 9. Докажите, что $I_n=I_0$‍.‍

Усложним задачу. Введём функцию $I(t)$‍,‍ равную произведению величины скорости $v(t)$‍‍ шарика на расстояние $l(t)$‍‍ между стенками в произвольный момент времени $t$‍.‍ Пусть $t_0$‍,‍ $t_1$‍,‍ $\ldots$‍‍ — моменты удара шарика о неподвижную стенку. Согласно утверждению задачи 9, $I(t_n)=І_0$‍‍ для всех $n\ge0$‍.‍ Однако при остальных значениях $t$‍‍ получаем $I(t)\ne I_0$‍.‍

Задача 10. Докажите неравенство $$ \left|\dfrac{I(t)-I_0}{I_0}\right|\le\dfrac V{v_0+V}. $$

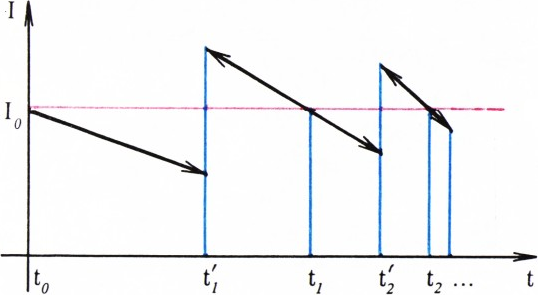
Подсказкой к решению этой задачи служит график функции I(t), изображённый на рисунке 4.

Следовательно, если скорость стенки много меньше скорости шарика ($V\ll v_0$‍),‍ то величина $I(t)$‍‍ будет очень мало отличаться от своего первоначального значения $I_0$‍.‍ В механике такие величины называются адиабатическими инвариантами (в термодинамике адиабатическим процессом называется процесс, проходящий без выделения и поглощения тепла).

Баллистический маятник

В качестве ещё одного применения законов удара рассмотрим задачу о баллистическом маятнике, с помощью которого измеряют скорости движущихся тел. Он состоит из трубы массой $M$‍,‍ заполненной песком и подвешенной на невесомом тросе длиной $l$‍‍ (рис. 5). Снаряд массой $m$‍,‍ попадая в трубу, застревает в песке. Происходит очень быстрая потеря скорости снаряда — абсолютно неупругий удар.

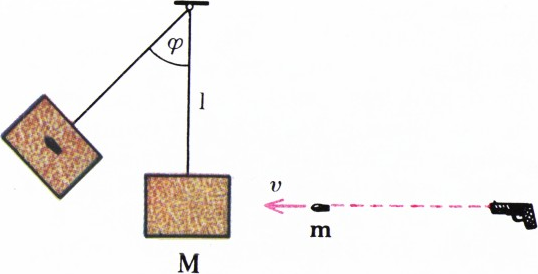
Задача 11. Зная максимальный угол отклонения трубы $\phi$‍,‍ найдите скорость снаряда.

Баллистический маятник изобретён английским механиком Робинсом и описан в книге «Новые принципы пушечной стрельбы» (1742).

Принцип относительности и закон сохранения импульса

Мы решили ряд конкретных задач из механики соударяющихся тел. Теперь снова можно обратиться к основным соотношениям теории удара и обсудить их смысл и происхождение.

В мемуаре Гюйгенса «О движении тел под воздействием удара» закон сохранения импульса выводится из принципа относительности Галилея. Мы воспроизведём рассуждения Гюйгенса для случая абсолютно неупругого удара.

Сначала напомним определение инерциальной системы отсчёта и формулировку принципа относительности. Под системой отсчёта будем понимать платформу, снабжённую линейкой и часами. С её помощью можно определять положение тел на прямой и течение времени. Предположим, что одна система отсчёта движется относительно другой с постоянной скоростью. Принцип относительности Галилея утверждает, что все законы механики (в том числе и законы удара) имеют в обеих системах отсчёта одинаковый вид. Этот принцип относительности является очень общим: он справедлив и в релятивистской механике. Специфика ньютоновской механики проявляется в том, как связаны системы отсчёта, движущиеся друг относительно друга с постоянной скоростью.

Эта связь выражается преобразованиями Галилея. Предположим, что в обеих системах производится наблюдение одного и того же тела. Пусть в первой системе отсчёта координата тела на прямой равна $x$‍,‍ а часы показывают время $t$‍;‍ во второй системе значения координаты и времени равны $x'$‍‍ и $t'$‍.‍ Если $v$‍‍ — постоянная скорость движения второй системы отсчёта относительно первой, то $$ x=x'+vt'+a,\quad t=\pm t'+b, $$ где $a$‍‍ и $b$‍‍ — некоторые константы.

Обратимся к выводу формулы (2) для абсолютно неупругого удара.

Рассуждения Гюйгенса включают анализ нескольких случаев.

а) Рассмотрим сначала простейшую ситуацию, когда сталкиваются два одинаковых тела с массами $m$‍,‍ двигавшиеся навстречу друг другу со скоростями $v$‍‍ и $-v$‍.‍ В силу предположения о неупругом характере удара тела слипаются, образуя одно тело массой $2m$‍.‍ По соображениям симметрии, это тело после удара будет покоиться.

б) Рассмотрим более сложный случай, когда сталкиваются две одинаковые массы $m$‍,‍ имеющие до момента удара произвольные скорости $v_1$‍‍ и $v_2$‍.‍ Перейдём к новой инерциальной системе отсчёта $S'$‍,‍ которая движется относительно исходной системы $S$‍‍ с постоянной скоростью $v=\dfrac{v_1+v_2}2$‍.‍ В системе $S'$‍‍ картина движения тел будет, как в случае а): тела одинаковой массы сближаются с равными по величине скоростями $\dfrac{v_1-v_2}2$‍‍ и $\dfrac{v_2-v_1}2$‍.‍ Согласно принципу относительности и заключению пункта а), после удара тело массой $2m$‍‍ будет покоиться в системе $S'$‍.‍ Следовательно, относительно исходной системы $S$‍‍ оно будет двигаться со скоростью $\dfrac{v_1+v_2}2$‍.‍ Итак, формула (2) установлена в случае, когда $m_1=m_2$‍.‍

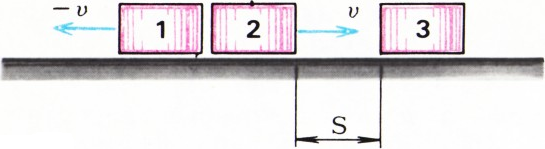
в) Пусть теперь имеются три одинаковых тела каждое массой $m$‍‍ (рис. 6). В начальный момент все они покоятся, причём тела 1 и 2 соприкасаются. Предположим, что тела 1 и 2 разлетаются в разные стороны (например, в результате взрыва). Ввиду симметрии их скорости будут равны по величине. Первое тело будет беспрепятственно двигаться влево со скоростью $-v$‍,‍ а второе будет двигаться вправо со скоростью $v$‍‍ и вскоре столкнётся с телом 3. Согласно результату пункта б), тело «$\textit{2}+\textit{3}$‍‍» массой $2m$‍‍ будет после удара двигаться вправо со скоростью $\dfrac v2$‍.‍ Если расстояние между телами очень мало, то столкновение и слипание тел 2 и 3 произойдёт практически мгновенно. Поэтому можно считать, что с самого начала тела 2 и 3 образовывали одно целое и мы приходим к следующему выводу: если в начальный момент времени два тела с массами $m$‍‍ и $2m$‍‍ соприкасались и затем начали разлетаться в разные стороны, то скорость тела массой $2m$‍‍ будет в два раза меньше скорости тела массой $m$‍.‍

г) Рассмотрим случай, когда два тела с массами $m$‍‍ и $2m$‍‍ движутся навстречу друг другу со скоростями $v$‍‍ и $-\dfrac v2$‍‍ соответственно. Утверждается, что после абсолютно неупругого удара слипшееся тело массой $3m$‍‍ будет покоиться (в соответствии с формулой (2)). Действительно, мы можем вообразить новую систему отсчёта $S'$‍,‍ в которой часы идут в «обратную сторону». Относительно системы $S'$‍‍ все тела будут двигаться в противоположном направлении с той же по абсолютной величине скоростью, поэтому нам остаётся воспользоваться принципом относительности и результатом пункта в).

д) Теперь обратимся к случаю, когда тела с массами $m$‍‍ и $2m$‍‍ движутся с произвольными скоростями $v_1$‍‍ и $v_2$‍.‍ Как и в рассуждении пункта б), перейдём к новой системе отсчёта $S'$‍,‍ которая движется относительно $S$‍‍ со скоростью $\dfrac{v_1+2v_2}3$‍.‍ Именно с этой скоростью движется их общий центр масс (проверьте!). В системе $S'$‍‍ центр масс тел $m$‍‍ и $2m$‍‍ покоится, тело $m$‍‍ подлетает к нему со скоростью $$ v_1'=\dfrac{v_1+2v_2}3-v_1=-\dfrac23(v_1-v_2), $$ а тело $2m$‍‍ — со скоростью $$ v_2'=\dfrac{v_1+2v_2}3-v_2=\dfrac13(v_1-v_2). $$ Мы видим, что относительные скорости $v_1'$‍‍ и $v_2'$‍‍ отличаются знаками и $|v_1'|=|2v_2'|$‍.‍ Следовательно, согласно пункту г), после столкновения тело массой $3m$‍‍ будет покоиться в системе $S'$‍,‍ а относительно исходной системы $S$‍‍ оно будет двигаться со скоростью $$ v=\dfrac{mv_1+2mv_2}{3m}=\dfrac{v_1+2v_2}3. $$ Таким образом, формула (2) установлена в случае, когда $m_2=2m_1$‍.‍

Рассуждая аналогично, мы можем обосновать формулу (2) для случая рационального отношения масс $m_1$‍‍ и $m_2$‍.‍ Её обоснование для иррациональных отношений $\dfrac{m_1}{m_2}$‍‍ носит уже формальный характер и связано со строгим введением понятия действительного числа. Дело здесь обстоит так же, как с выводом формулы площади прямоугольника со сторонами $a$‍‍ и $b$‍:‍ для соизмеримых $a$‍‍ и $b$‍‍ прямоугольник можно разбить на одинаковые квадраты, а если $a$‍‍ и $b$‍‍ несоизмеримы, то нужно использовать приближение иррациональных чисел рациональными.

С математической точки зрения рассуждения Гюйгенса, быть может, нельзя признать вполне строгими. Но мы и не стремились дать строгое доказательство формулы для абсолютно неупругого удара. У нас была иная цель: показать, что идеи Гюйгенса с необходимостью приводят к закону сохранения импульса. Подчеркнём, что мы исходили лишь из принципа относительности Галилея и не использовали основные принципы динамики Ньютона (например, закон равенства действия и противодействия). Рассуждение Гюйгенса показывает, что закон сохранения импульса следует из симметричности (или инвариантности) законов механики относительно преобразований Галилея. Это отражает общий факт: всякая симметрия законов механики приводит к своему закону сохранения. Например, инвариантность относительно поворотов пространства влечёт закон сохранения момента импульса, а инвариантность относительно сдвигов оси времени — закон сохранения энергии. Общая теорема, связывающая симметрии с законами сохранения, была открыта знаменитым немецким математиком Эмми Нётер (1882‍—‍1935).