Изображения страниц
Текст статьи Ивлев Б. М. Избранные школьные задачи // Квант. — 1985. — № 10. — С. 24.
Восьмой класс
- При каких натуральных
$n$ сократима дробь$\dfrac{8n+71}{5n+46}$? - Решите уравнение
$x^2+\dfrac{9x^2}{(x+3)^2}=16$. - В окружности радиуса
$R$ проведены два диаметра, угол между которыми равен$\alpha$. Докажите, что расстояние между основаниями перпендикуляров, опущенных из произвольной точки окружности на эти диаметры, не зависит от положения точки на окружности, и найдите его. - Докажите, что число
$n^2+5n+16$ ни при каком натуральном$n$ не делится на 169. - Постройте квадрат, если даны 4 точки: по одной точке на каждой из прямых, содержащих стороны квадрата.
Девятый класс
- Разложите на множители выражение
$$
(1+x+x^3+x^3+\ldots+x^n)^2-x^n,
$$
где
$n$ — натуральное число,$n\ge3$. - Высоты треугольника пересекаются в точке
$H$. Известно, что$|HC|=|AB|$. Найдите угол при вершине$C$. В пространстве даны две скрещивающиеся прямые
$a$ и$b$. Проведите прямую, пересекающую обе данные прямые и:- проходящую через данную точку
$M$, не лежащую на$a$ и$b$; - параллельную данной прямой
$l$.
В каком случае решение возможно?
- проходящую через данную точку
- При каком условии прямые
$y=k_1x+b_1$ и$y=k_2x+b_2$ перпендикулярны? - Найдите кратчайшее расстояние от точек параболы
$y=x^2-8x+16$ до прямой$y=-2x+1$.
- При каком условии прямые
- В пространстве даны две скрещивающиеся взаимно перпендикулярные прямые
$a$ и$b$. Найдите множество середин отрезков$AB$ данной длины$d$ таких, что$A\in a$, $B\in b$.
Десятый класс
- Как нужно разместить в пространстве правильный тетраэдр,
чтобы его ортогональная проекция на данную плоскость имела наибольшую
площадь? Найдите значение этой площади, если ребро тетраэдра имеет длину
$a$. - Решите уравнение $$ \log_2^2(x+y)+\log_2^2(xy)+1=2\log_2(xy). $$
- Докажите формулу Симпсона: пусть площадь сечения тела
плоскостью
$P_x$, проведённой перпендикулярно координатной оси$Ox$ через точку этой оси с координатой$x$, выражается при$x\in[a;b]$ многочленом от$x$ не выше третьей степени (тело заключено между плоскостями$P_a$ и$P_b$); тогда объём$V$ тела можно вычислить по формуле $$ V=\dfrac h6(S_a+4S_{\text{ср}}+S_b), $$ где$h=b-a$, $S_a=S(a)$, $S_b=S(b)$, $S_{\text{ср}}$ — площадь «среднего» сечения — сечения плоскостью$P_{\frac{\scriptstyle a+b}{\scriptstyle2}}$, соответствующего координате$x_0=\dfrac{a+b}2$. - Дан прямоугольный параллелепипед, основание которого — квадрат
$ABCD$ со стороной 10, боковое ребро$AA_1$ имеет длину 40. Пусть$P$ — середина$AB$, $Q$ — середина$CD$, $E$ — точка, принадлежащая$PQ$ и удалённая от стороны$AB$ на расстояние 1. Найдите длину кратчайшего пути, проходящего по поверхности этого параллелепипеда и соединяющего точку$E$ с точкой$F$, симметричной точке$F$ относительно центра параллелепипеда. - Решите уравнение $$ \sqrt[\scriptstyle4]{a-x\vphantom2}+\sqrt[\scriptstyle4]{b-x\vphantom2}= \sqrt[\scriptstyle4]{a+b-2x}. $$
Ответы, указания, решения
$n=13k-4$, где$k$ — натуральное число. Решение. Заметим, что $$ \dfrac{8n+71}{5n+46}=1+\dfrac{3n+25}{5n+46}, $$ поэтому исходная дробь сократима в том и только в том случае, когда сократима дробь$\dfrac{3n+25}{5n+46}$, а следовательно, и дробь$\dfrac{5n+46}{3n+25}$. Далее последовательно получаем, что сократимость исходной дроби эквивалентна сократимости дробей$\dfrac{3n+24}{2n+21}$ $\Big($ так как$\dfrac{5n+46}{3n+25}=1+\dfrac{2n+21}{3n+25}\Big)$, $\dfrac{2n+21}{n+4}$ $\Big($ так как$\dfrac{3n+25}{2n+21}=1+\dfrac{n+4}{2n+21}\Big)$ и$\dfrac{13}{n+4}$ $\Big($ так как$\dfrac{2n+21}{n+4}=2+\dfrac{13}{n+4}\Big)$. Последняя из полученных дробей сократима тогда и только тогда, когда её знаменатель делится на 13.$1\pm\sqrt7$. Решение.$$ x^2+\dfrac{9x^2}{(x+3)^2}=\dfrac{x^4+6x^3+18x^2}{(x+3)^2}= \dfrac{x^4}{(x+3)^2}+\dfrac{6x^2}{x+3}. $$ Обозначив$\dfrac{x^2}{x+3}$ через$y$, получим ypaвнeние$y^2+6y-16=0$, корни которого$y_1=-8$ и$y_2=2$. Осталось решить уравнения замены$\frac{x^2}{x+3}=2$ и$\dfrac{x^2}{x+3}=-8$, второе из которых не имеет решений.$R\sin\alpha$. Решение. Угол$M_1MM_2$, равен либо$\alpha$ (рис. 1, a), либо$180^\circ-\alpha$ (рис. 1, б), так как его стороны перпендикулярны данным диаметрам. Далее, точка$M_1$ лежит на окружности диаметра$MO$: если$M_1$ совпадает с$O$, то это очевидно, а если$M_1$ не совпадает с$O$, то это следует из того, что угол$MM_1O$ прямой. Аналогично показывается, что$M_2$ лежит на окружности диаметра$MO$. Итак, угол$M_1MM_2$ вписан в окружность радиуса$R_1=\dfrac{MO}2=\dfrac R2$ и равен либо$\alpha$, либо$180^\circ-\alpha$, поэтому длина хорды$M_1M_2$ равна$2R_1\sin\alpha=R\sin\alpha$ (см. «Геометрия 6—10», § 11, с. 147).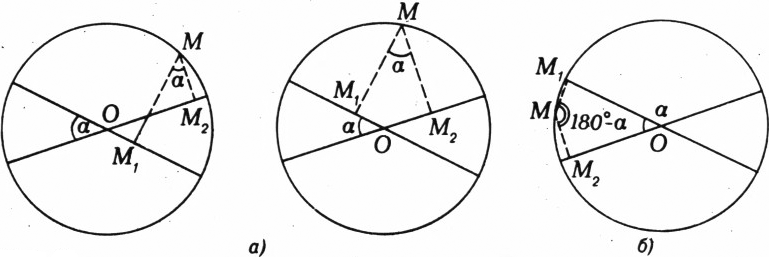
Рис. 1 Заметим, что
$n^2+5n+16=(n-4)^2+13n$. Это число заведомо должно делиться на 13, поэтому n-4 должно делиться на 13, тогда$(n-4)^2$ делится на 169, а второе слагаемое$13n$ не делится на 169 (так как$n$ не делится на 13).-
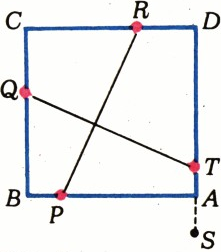
Рис. 2 Указание. Пусть точки
$P$, $Q$, $R$, $S$ лежат на прямых$AB$, $BC$, $CD$, $DA$ соответственно (рис. 2). Отложим от точки$Q$ отрезок$QT$, равный по длине и перпендикулярный отрезку$PR$ (из двух направлений на прямой$QT$ выбирается такое, что точка$T$ лежит в правой полуплоскости с границей$BC$). Тогда точка$T$ лежит на прямой$DA$, и для её построения достаточно соединить точки$S$ и$T$. Если$T$ и$S$ совпадают, то в качестве$DA$ можно взять любую прямую, проходящую через$S$. $(1+x+x^2+\ldots+x^{n-1})(1+x+x^2+\ldots+x^{n+1})$. Решение. Предположим, что$x\ne1$ и воспользуемся формулой суммы геометрической прогрессии: $$ 1+x+x^2+\ldots+x^n=\dfrac{1-x^{n+1}}{1-x}. $$ Получаем, что рассматриваемое выражение равно $$ \left(\dfrac{1-x^{n+1}}{1-x}\right)^2-x^n=\dfrac{(1-x^n)(1-x^{n+2})}{(1-x)^2}= \dfrac{1-x^n}{1-x}\cdot\dfrac{1-x^{n+2}}{1-x} $$ (при$x\ne1$). Случай$x=1$ очевиден.$45^\circ$ или$135^\circ$. Решение. Обозначим основания высот, проведённых к сторонам$AB$, $BC$, $CA$, через$C_1$, $A_1$ и$B_1$ соответственно (рис. 3). Если угол$C$ острый, то из равенства прямоугольных треугольников$ABB_1$ и$CHB_1$ (у них равны гипотенузы$AB$ и$CH$ по условию и острые углы$ABB_1$ и$HCB_1$ — каждый из них равен$90^\circ-\alpha$, см. рис. 3, а, б) получаем$BB_1=B_1C$. В прямоугольном треугольнике$BB_1C$ катеты$BB_1$ и$B_1C$ равны, поэтому каждый из углов$CBB_1$ и$B_1CB$ равен$45^\circ$. Если угол$C$ тупой (см. рис. 3, в), то равны треугольники$ABA_1$ и$CHA_1$, поэтому$BA_1=A_1H$ и$\angle BHA_1=45^\circ$, а$\angle ACB=\angle A_1CB_1=135^\circ$ (в четырёхугольнике$A_1CB_1H$: $\angle H=45^\circ$, $\angle A_1=\angle B_1=90^\circ$). 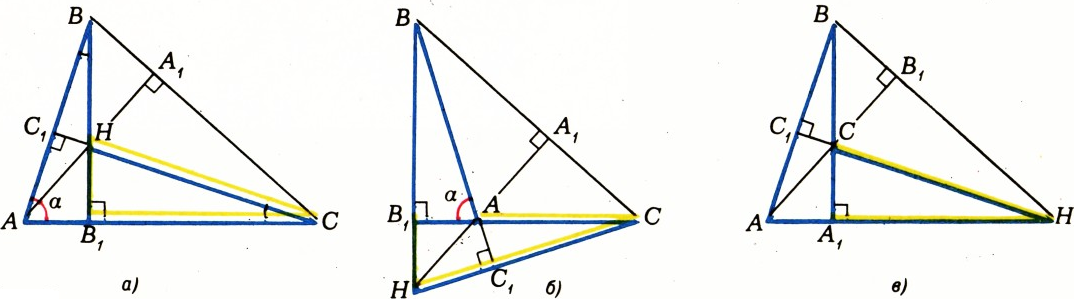
Рис. 3 Указание. Прежде всего отметим, что существует, притом только одна, пара (параллельных) плоскостей
$\alpha$ и$\beta$, такая, что$a$ лежит в$\alpha$, $b$ лежит в$\beta$ и$b\parallel\alpha$, $a\parallel\beta$. Любая прямая, пересекающая$a$ и проходящая через$M$ (параллельная$l$), лежит в некоторой плоскости$\pi$ (в п. а) — это плоскость, проходящая через$a$ и$M$, в п. б) — это плоскость, проходящая через$a$ и параллельная$l$). Если$\pi$ не совпадает с$\alpha$, то прямая$b$ пересекается с$\pi$ в некоторой точке$N$. Искомая прямая должна совпадать с прямой$MN$. Прямая$MN$ всегда пересекается с$b$ (в точке$N$) и лежит с$a$ в одной плоскости (плоскости$\pi$), поэтому$MN$ и$a$ либо параллельны, либо пересекаются. Легко понять, что$MN\parallel a$ только в том случае, когда$MN$ принадлежит$\beta$ (в п. a)); соответственно,$l$ параллельна$\beta$ (в п. б)). Следовательно, решение задачи существует, если$M$ не лежит ни в$\alpha$, ни в$\beta$ в п. а), и если$l$ не параллельна$\alpha$ и$\beta$ в п. б).а)
$k_1k_2=-1$; б)$\dfrac6{\sqrt5}$. - Угловой коэффициент прямой
$y=kx+b$ — это тангенс угла наклона этой прямой к оси абсцисс. Проведём к параболе
$f(x)=x^2-8x+16$ касательную, параллельную прямой$y=-2x+1$ (рис. 4). Для этого найдём абсциссу точки касания:$f'(x)=2x-8$; $2x-8=-2$ при$x=3$, уравнение касательной$y=-2x+7$. Эта касательная пересекает ось абсцисс в точке$(3{,}5;0)$. Парабола лежит по одну сторону от этой касательной, поэтому кратчайшее расстояние равно длине перпендикуляра, опущенного из точки касания (точки$(3;1)$) на прямую$y=-2x+1$. Это расстояние равно расстоянию между прямыми$y=-2x+1$ и$y=-2x+7$. Его проще всего найти из прямоугольного треугольника$ABC$: пусть$AB=z$, тогда$BC=0{,}5z$, поскольку$\tg\angle BCA=2$; поэтому$z^2+\dfrac14z^2=9$, откуда$z=\dfrac6{\sqrt5}$. 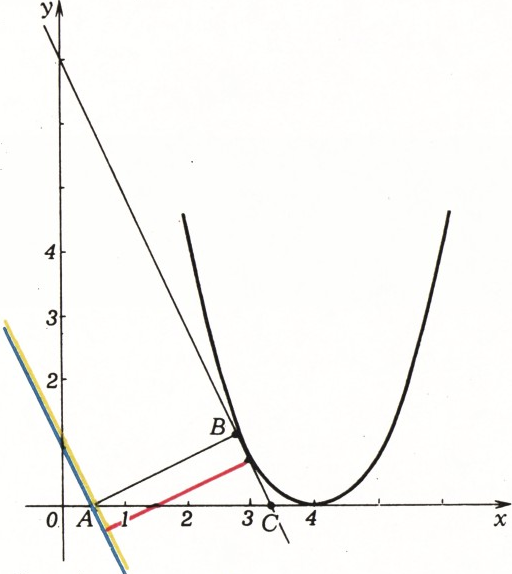
Рис. 4
- Угловой коэффициент прямой
Окружность диаметра
$\sqrt{d^2-h^2}$, где$h$ — длина общего перпендикуляра$PQ$ к прямым$a$ и$b$, центр окружности — середина этого перпендикуляра, плоскость окружности перпендикулярна$PQ$. Указание. Множество cepeдин отрезков$AB$, где$A$ принадлежит$a$, $B$ принадлежит$b$, — плоскость, проходящая через середину общего перпендикуляра к прямым$a$ и$b$ и перпендикулярная ему. Поэтому искомое множество лежит в этой плоскости. Спроектируем ортогонально на эту плоскость один из данных отрезков — отрезок$AB$ (рис. 5); получим отрезок$A_1B_1$. $AA_1BB_1$ — параллелограмм, так как отрезки$AA_1$ и$BB_1$ параллельны и равны (длина каждого из них равна$h$). Из прямоугольного треугольника$AA_1M$, где$M$ — cepeдина$AB$, найдём, что$MA_1=\sqrt{d^2-h^2}$. Далее, в прямоугольном треугольнике$A_1OB_1$ точка$M$ — середина гипотенузы, поэтому$OM=A_1M=\dfrac12\sqrt{d^2-h^2}$, откуда следует, что точка$M$ принадлежит окружности с центром$O$ радиуса$\dfrac12\sqrt{d^2-h^2}$, расположенной в плоскости$A_1OB_1$. Осталось проверить, что любая точка этой окружности — середина одного из отрезков, фигурирующих в условии задачи.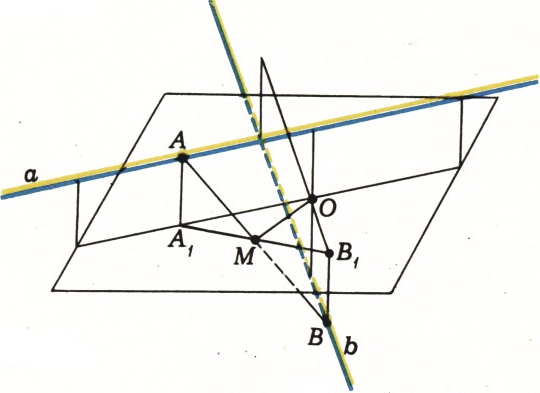
Рис. 5 $\dfrac{a^2}2$; плоскость проекции должна быть параллельна любым двум противоположным рёбрам тетраэдра. Указание. Проекцией тетраэдра будет либо треугольник, либа четырёхугольник. В первом случае площадь проекции будет совпадать с проекцией одной из граней; при этом площадь проекции будет равна$S\cos\phi$, где$S=\dfrac{a^2\sqrt3}4$ — площадь грани правильного тетраэдра,$\phi$ — угол между плоскостью этой грани и плоскостью проекции. В этом случае наибольшее значение площади проекции равно$\dfrac{a^2\sqrt3}4$ ‚ когда$\cos\phi=1$. Во втором случае диагонали четырёхугольника — проекции противоположных рёбер тетраэдра (рёбер$AD$ и$BC$ на рисунке 6). По известной формуле площадь этого четырёхугольника равна$\dfrac12bc\sin\psi$, где$b$ и$c$ — диагонали четырёхугольника,$\psi$ — угол между ними. Диагонали четырёхугольника — проекции рёбер тетраэдра, и их длины равны$a\cos\theta_1$ и$a\cos\theta_2$, где$\theta_1$ и$\theta_2$ — углы между этими рёбрами и плоскостью проекции, поэтому$b\le a$, $c\le a$ и$S\le\dfrac12a^2\sin\psi\le\dfrac{a^2}2$; при этом равенства достигаются в случае, когда$\cos\theta_1=\cos\theta_2=\sin\psi=1$. 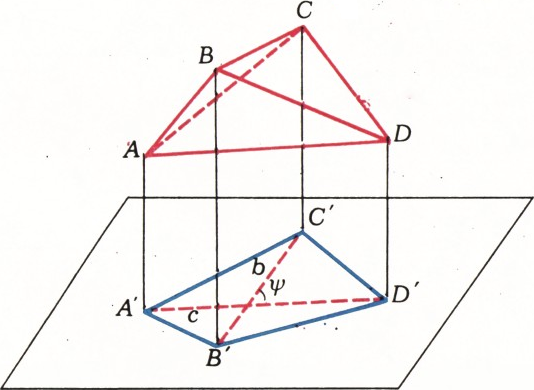
Рис. 6 $x=y=1$. Решение. Запишем уравнение в виде $$ \log_2^2(xy)+(\log_2(x+y)-1)^2=0. $$ Это равенство возможно только в том случае, когда имеет место система уравнений $$ \left\{\,\colsep{0pt}{\begin{array}{l}\log_2(xy)=0,\\\log_2(x+y)=1\end{array}} \right.\enspace\Leftrightarrow\enspace \left\{\,\colsep{0pt}{\begin{array}{l}xy=1,\\x+y=2,\end{array}}\right. $$ откуда$x=y=1$. Указание.$$ \begin{gathered} \textstyle\int\limits_a^b{}(C_1+C_2x+C_3x^2+C_4x^3)\,dx=\\ =\textstyle C_1\int\limits_a^bdx+C_2\int\limits_a^bx\,dx+C_3\int\limits_a^b x^2\,dx+C_4\int\limits_a^bx^3\,dx, \end{gathered} $$ поэтому достаточно проверить справедливость формулы Симпсона для функций 1,
$x$, $x^2$ и$x^3$. $\sqrt{2164}\approx46{,}52$. Указание. Рассмотрим путь, соединяющий$E$ с$F$ на развёртке параллелепипеда. Достаточно сравнить пути$|EF_1|$, $|EF_2|$, $|EF_3|$, $|EF_4|$ (рис. 7; можно считать, что развёртка боковых граней и квадрата, содержащего$E$, зафиксированы, и рассмотреть четыре варианта развёртки оставшегося квадрата). По теореме Пифагора легко подсчитать, что $$ \begin{aligned} |EF_1|=|EF_2|&=\sqrt{46^2+14^2}=\sqrt{2312};\\ |EF_4|&=\sqrt{42^2+20^2}=\sqrt{2164}. \end{aligned} $$ Кроме того, очевидно, что$|EF_2|=50$. 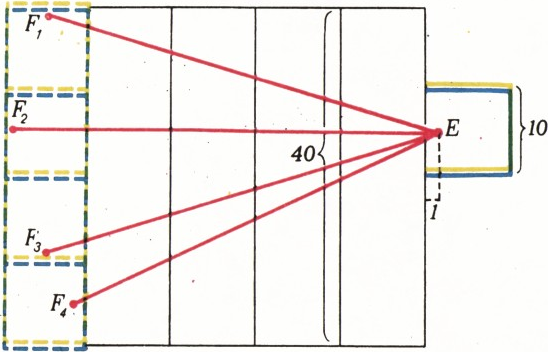
Рис. 7 $x=c$, где$c$ — это меньшее из чисел$a$ и$b$. Решение. Обозначим$a-x$ через$y^4$, $b-x$ через$z^4$, тогда$a+b-2x=y^4+z^4$. После этого уравнение запишется в виде$y+z=\sqrt[\scriptstyle4]{y^4+z^4}$. Возведём обе части этого уравнения в четвёртую степень; после преобразований получим уравнение$yz(2y^2+3yz+2z^2)=0$, откуда либо$z=0$, либо$y=0$, либо$2y^2+3yz+2z^2=0$. При$z\ne0$ уравнение$2y^2+3yz+2z^2=0$ можно записать в виде$2{\left(\dfrac yz\right)}^2+3{\left(\dfrac yz\right)}+2=0$. Получившееся квадратное уравнение$\Big($ относительно переменной$\dfrac yz\Big)$ не имеет решений. Итак, либо$y=0$, откуда$x=a$, либо$z=0$, откуда$x=b$. Проверка показывает, что из двух полученных значений годится только меньшее.







