Изображения страниц
Текст статьи Задачи наших читателей // Квант. — 1982. — № 3. — С. 58.
Докажите, что если
$1\le x\le5$, то уравнение$x^n+y^n=z^n$ не имеет решений в натуральных числах.Разложите на множители многочлен
$x^8+4x^2+4$. Пусть
$S(n)$ — сумма цифр в двоичной записи натурального числа$n$. Докажите, что среди пар$(m;n)$ различных натуральных чисел$m$ и$n$ найдётся бесконечное множество таких, что$\dfrac m{S(m)}=\dfrac n{S(n)}$. Решите аналогичную задачу для десятичной системы.В треугольнике сумма квадратов длин сторон равна
$m^2$, а сумма их четвёртых степеней равна$n^4$. Найдите площадь этого треугольника.- Докажите, что для каждого
$n\ge3$ на плоскости существует$n$ окружностей с различными центрами такие, что любой отрезок, соединяющий центры двух окружностей, пересекают хотя бы одну окружность с другим центром. - Докажите, что существует такое
$m$, что на плоскости нельзя расположить$m$ окружностей так, чтобы любой отрезок, соединяющий центры двух окружностей, пересекался с остальными$m-2$ окружностями. - Попробуйте найти наименьшее такое
$m$. (Решение автору неизвестно.)
- Докажите, что для каждого
- Вместо переменных
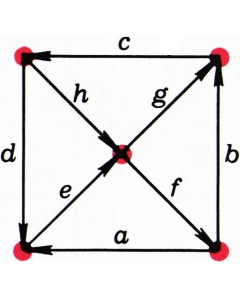
$a$, $b$, $c$, $d$, $e$, $f$, $g$, $h$ (рис. 1) расставьте первые восемь натуральных чисел так, чтобы сумма потоков, втекающих в каждый из пяти узлов (на рисунке 1 узлы отмечены красным цветом), была равна сумме вытекающих потоков. Сколько решений имеет задача? - Докажите, что подобная расстановка чисел 1, 2,
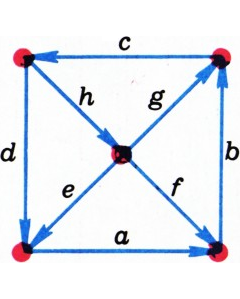
$\ldots$, 8 для рисунка 2 невозможна.
- Вместо переменных
Тонкое проволочное кольцо вращается с угловой скоростью
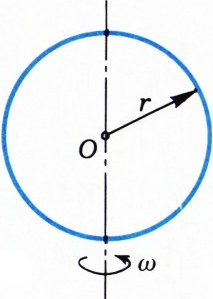
$\omega$ вокруг оси, проходящей через центр кольца и лежащей в его плоскости (рис. 3). Масса кольца$M$, его радиус$r$. Определите кинетическую энергию кольца.Пусть
$p\ne2$ — простое число. Рассмотрим все натуральные числа, меньшие$p$. Обозначим через$S_1$, $S_2$, $S_3$, $\ldots$, $S_{p-2}$ суммы произведений, составленных из этих чисел, взятых по одному, по два, по три и т. д., т. е. $$ \begin{align*} S_1&=1+2+3+\ldots+(p-1),\\ S_2&=1\cdot2+1\cdot3+\ldots+(p-2)\cdot(p-1),\\ S_3&=1\cdot2\cdot3+1\cdot2\cdot4+\ldots+(p-3)\cdot(p-2)\cdot(p-1),\\ &{\ldots}\,{\ldots}\,{\ldots}\,{\ldots}\,{\ldots}\,{\ldots}\,{\ldots}\\ S_{p-2}&=1\cdot2\cdot3\cdot\ldots\cdot(p-2)+ 1\cdot3\cdot\ldots\cdot(p-2)\cdot(p-1)+\ldots+ 2\cdot3\cdot\ldots\cdot(p-2)\cdot(p-1). \end{align*} $$- Докажите, что все эти суммы делятся на
$p$. Указание. Воспользуйтесь таким утверждением: если многочлен с целыми коэффициентами степени меньше$p$ делится на$p$ во всех целых точках, то все его коэффициенты делятся на$p$. - Докажите, что суммы
$S_3$, $S_5$, $S_7$, $\ldots$, $S_{p-2}$ делятся на$p^2$.
Эта задача — для тех, кто умеет обращаться с биномиальными коэффициентами (см., например, статью Н. Васильева и А. Зелевинскогов № 1).
- Докажите, что все эти суммы делятся на
Ответы, указания, решения
- Доказательство основано на неравенстве
$(a+b)^n\gt a^n+nba^{n-1}$, а в случае$x=5$, кроме того, на небольшом переборе. $x^8+4x^2+4=(x^4-2x^3+2x^2-2x+2)(x^4+2x^3+2x^2+2x+2)$. Равенство
$\dfrac m{S(m)}=\dfrac n{S(n)}$ выполнено при$m=69=1000101_2$ и$n=92=1011100_2$. Поэтому множество$A$ натуральных чисел$k$, удовлетворяющих равенству$\dfrac{3k}{S(3k)}=\dfrac{4k}{S(4k)}$, нe пусто (последнее равенство выполнено при$k=23$). Покажем, что множество$A$ бесконечно.Если
$k\in A$, $k=a_1a_2\ldots a_p$ — двоичная запись числа$k$ и, аналогично,$3k=b_1b_2\ldots b_q$ ($q=p+1$ или$p+2$), то $$ \colsep{0pt}{\begin{array}{clllll} &a_1&a_2&{}\ldots{}&a_p&0\\[-6pt] +\\[-6pt] &&a_1&{}\ldots{}&a_{p-1}&a_p\\[1pt] \hline &b_1&b_2&{}\ldots{}&b_{q-1}&b_q \end{array}} $$ Возьмём$l\ge0$ и рассмотрим числа $$ N=(2^{p+l+2}+1)k=a_1\ldots a_00\overbrace{0\ldots0}^l0a_1\ldots a_p. $$ Двоичное разложение числа$3N$ получается как результат сложения $$ \colsep{0pt}{\begin{array}{clllllcllllll} &a_1&a_2&{}\ldots{}&a_p&0&0\ldots0&0&a_1&a_2&{}\ldots{}&a_p&0\\[-6pt] +\\[-6pt] &&a_1&{}\ldots{}&a_{p-1}&a_p&0\ldots0&0&0&a_1&{}\ldots{}&a_{p-1}&a_p\\[1pt] \hline &b_1&b_2&{}\ldots{}&b_{q-1}&b_q&\underbrace{0\ldots0}_i&&b_1&b_2&{}\ldots{}&b_{q-1}&b_q\\ \end{array}}, $$ где$i=l$ или$l+1$. Отсюда$S(3N)=2S(3k)$. Кроме того,$S(4N)=2S(4k)$. Поэтому$N\in A$. $\dfrac{\sqrt{m^4-2n^4}}4$. Если направления всех потоков на рисунке 1 (в условии) заменить на противоположные, получится фигура, совпадающая с зеркальным отражением данной относительно вертикальной оси. Поэтому каждому решению соответствует симметричное. Шесть решений показаны на рисунке 2 (ещё шесть им симметричны).
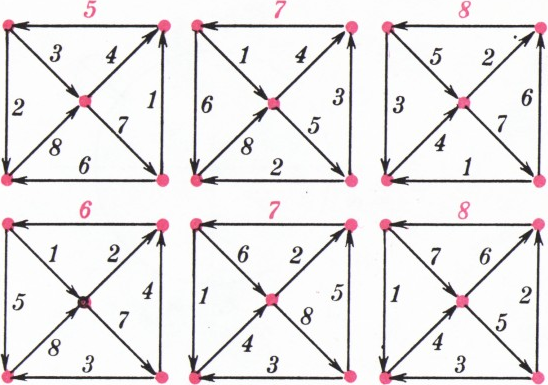
Рис. 2 - По условию должно быть
$c=d+h$, $h=e+f+g$, т. е.$c=d+e+f+g$. Но даже$1+2+3+4\gt8$. Поэтому требуемая расстановка невозможна.
Докажем следующую теорему: кинетическая энергия плоского тела, вращающегося вокруг оси, перпендикулярной плоскости тела, равна сумме кинетических энергий вращения (с той же угловой скоростью) вокруг взаимно перпендикулярных пересекающихся осей, лежащих в плоскости тела.
Доказательство. Кинетическая энергия тела, вращающегося с угловой скоростью
$\omega$, равна $$ K=\dfrac12\sum_im_i\omega^2r_i^2=\dfrac{\omega^2}2\sum_im_ir_i^2, $$ где$m_i$ — масса$i$ -й точки тела,$r_i$ — расстояние от$i$ -й точки до оси вращения. Если вращение происходит вокруг оси$l_1$ (рис. 3), то $$ K_{l_1}=\dfrac{\omega^2}2\sum_im_ir_{il_1}^2. $$ Ho$r_{il_1}^2=r_{il_2}^2+r_{il_3}^2$. Так что $$ K_{l_1}=\dfrac{\omega^2}2\sum_im_ir_{il_2}^2+ \dfrac{\omega^2}2\sum_im_ir_{il_3}^2, $$ т. е. $$ K_{l_1}=K_{l_2}+K_{l_3}, $$ что и требовалось доказать.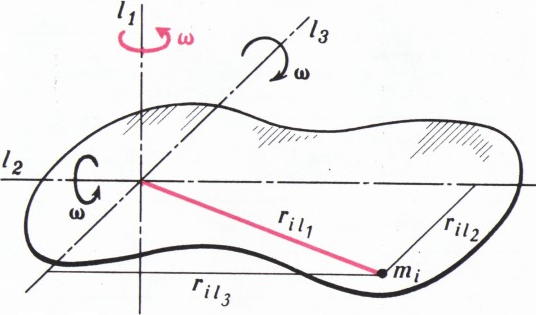
Рис. 3 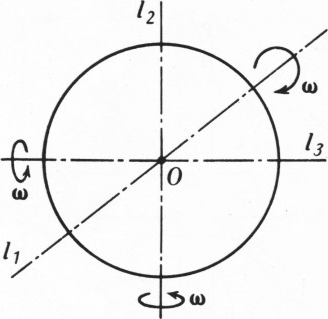
Рис. 4 Теперь вернёмся к кольцу. Кинетическая энергия кольца, вращающегося вокруг своей оси (оси
$l_1$; рис. 4), равна$K_{l_1}=\dfrac{m\omega^2r^2}2$ (кольцо однородно по массе и все его точки находятся на одном и том же расстоянии от оси$l_1$, поэтому$\sum\limits_im_ir_i^2=mr^2\Big)$. При вращении же вокруг осей$l_2$ и$l_3$ кинетические энергии, очевидно, одинаковы. Так что $$ K_{l_2}=K_{l_3}=\dfrac{K_{l_1}}2=\dfrac{m\omega^2r^2}4. $$ Это и есть искомая кинетическая энергия.- Рассмотрим два многочлена степени
$p$ с целыми коэффициентами: многочлен$x(x+1)(x+2)\ldots(x+(p-1))$ и многочлен$x^p-x$. Первый многочлен, очевидно, делится на$p$ при всех целых$x$, второй делится на$p$ при всех целых$x$ согласно малой теореме Ферма (см. «Квант», 1978, № 10, с. 7 или «Квант», 1972, № 10, с. 2). Разность этих многочленов — многочлен с целыми коэффициентами степени меньше$p$, делящийся на$p$ при всех целых$x$. Поэтому его коэффициенты делятся на$p$. Но эти коэффициенты — интересующие нас суммы. - Суммы
$\sum\limits_{1\le k_1\lt k_2\lt\ldots\lt k_q\le p-1} \prod\limits_{i=1}^qk_i$ и$\sum\limits_{1\le k_1\lt k_2\lt\ldots\lt k_q\le p-1} \prod\limits_{i=1}^q{}(p-k_i)$ отличаются только порядком слагаемых (если$k\lt p$, то и$p-k\lt p$). Поэтому при нечётном$q$ ($3\le q\le p-2$) $$ \begin{gathered} \textstyle S_q=\sum\limits_{1\le k_1\lt k_2\lt\ldots\lt k_q\le p-1} \prod\limits_{i=1}^qk_i=\sum\limits_{1\le k_1\lt k_2\lt\ldots\lt k_q\le p-1} \prod\limits_{i=1}^q{}(p-k_i)=\\ \textstyle=C_{p-1}^qp^q+\sum\limits_{j=1}^{q-1}{}(-1)^jC_{p-1-j}^{q-j}p^{q-j} S_j-S_q, \end{gathered} $$ т. е. $$ \textstyle 2S_q=C_{p-1}^qp^q+\sum\limits_{j=1}^{q-1}{} (-1)^jC_{p-1-j}^{q-j}p^{q-j}S_j, $$ откуда, учитывая, что все$S_j$ делятся на$p$, получаем, что$S_q$ делится на$p^2$.
- Рассмотрим два многочлена степени



