Изображения страниц
Текст статьи Задачи наших читателей // Квант. — 1981. — № 9. — С. 62.
Не пользуясь таблицами, докажите неравенство $$ \dfrac1{\log_2\pi}+\dfrac1{\log_5\pi}\gt2. $$
Найдите все числа вида
$\overline{a\underbrace{xx\ldots x\vphantom y}_n\underbrace{yy\ldots y}_nb}$ ($n=0$, 1, 2,$\ldots$), являющиеся полными квадратами.Найдите
- пять последних цифр числа
$15^{1981}$; - шесть последних цифр числа
$5^{1981}$; - семь последних цифр числа
$15^{1983}$.
- пять последних цифр числа
Докажите, что если
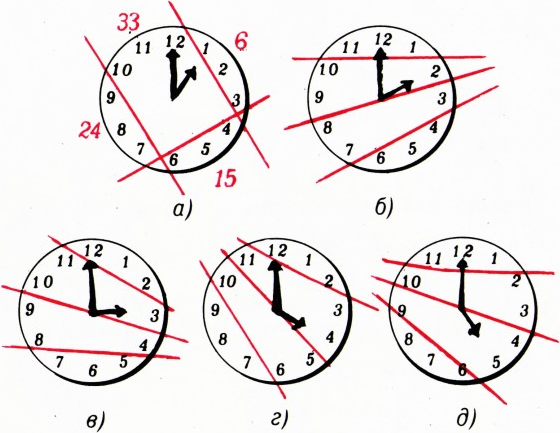
$n$ делится на$11^k-1$, то число$A=1\ldots1$, состоящее из$2n$ единиц, делится на$11^k$. Проведя три прямые, разделите циферблат часов (см. рисунок) на четыре участка, содержащие по три числа так, чтобы суммы чисел в каждом из участков были кратны трём и образовывали арифметическую прогрессию. Сколькими способами это можно сделать?
Ответы, указания, решения
- 16, 1156, 111556,
$\ldots$; 49, 4489, 444889,$\ldots$ a) 59375; б) 703125; в) 0859375.
Указание.
$15^{1981}=15^{247\cdot8+5}=15^5((15^{247}-1)(15^{247}+1)(15^{247\cdot2}+1)(15^{247\cdot4}+1)+1)=10^5\cdot A+15^5$. $5^{1981}=5^{123\cdot16+13}=5^{13}((5^{123}-1)(5^{123}+1)(5^{123\cdot2}+1)(5^{123\cdot4}+1)(5^{123\cdot8}+1)+1)=10^6\cdot B+5^{13}$. $15^{1983}=15^{247\cdot8+7}=10^7\cdot C+15^7$.
- Доказательство — индукцией по
$k$. При$k=1$ утверждение тривиально. Пусть оно верно для всех показателей степени, меньших$k$. Пусть$n=11^{k-1}\cdot m$, тогда $$ A=\underbrace{11\ldots1}_{2\cdot11^{k-1}\cdot m}= \underbrace{11\ldots1}_{2\cdot11^{k-2}\cdot m}\cdot B, $$ где$B=1\underbrace{00\ldots0}_{\mathclap{2\cdot11^{k-2}\cdot m-1}} 1\underbrace{00\ldots0}\ldots1$ — число, coстоящее из одиннадцати единиц, стоящих на нечётных местах, и нулей между ними (в количестве$2\cdot11^{k-2}\cdot m-1$ штук). Число$B$ делится на 11 (докажите это!), а число$\underbrace{11\ldots1}_{2\cdot11^{k-2}\cdot m}$ делится на$11^{k-1}$ по предположению индукции. Значит,$A$ делится на$11^k$. - См. рис. Получаются прогрессии 6, 15, 24, 33 и 15, 18, 21, 24 (четыре случая).