Изображения страниц
Текст статьи Кордемский Б. А. Семнадцать задач на смекалку // Квант. — 1981. — № 7. — С. 44—45.
Среди задач, предлагаемых пособиями для поступающих в вузы, встречаются и такие, при решении которых можно проявить находчивость и остроумие.
Разумеется, как правило, эти задачи можно решать и стандартными методами, однако решения, использующие нестандартные, остроумные соображения, часто оказываются более короткими и красивыми, чем традиционные.
Несколько таких задач мы предлагаем нашим читателям.
Задача 1. Пройдя
Задача 2. Из пункта
Задача 3. В колбе имеется раствор соли. Из колбы отливают
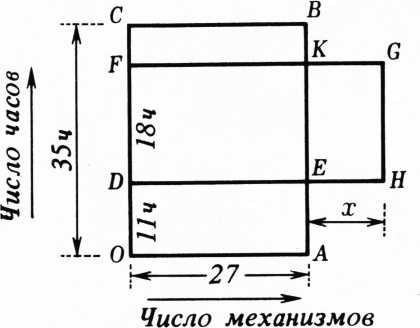
Задача 4. 27 одинаковых механизмов могут выполнить определённое задание за 35 часов непрерывной работы. Но через 11 часов к выполнению этого задания подключили ещё несколько таких же механизмов, и работа была закончена на 6 часов раньше. Сколько механизмов было подключено дополнительно?
Задача 5. От двух кусков сплава одинаковой массы, но с различным процентным содержанием меди отрезали по куску равной массы. Каждый из отрезанных кусков сплавили с остатком другого куска, после чего процентное содержание меди в обоих кусках стало одинаковым. Во сколько раз отрезанный кусок меньше целого куска?
Задача 6. Имеются два сплава серебра и золота: в одном
количества этих металлов находятся в отношении
Задача 7. На стороне
Задача 8. Дан
- Докажите, что существует треугольник
$A_1B_1C_1$, длины сторон которого равны длинам медиан треугольника ABC. - Докажите, что треугольник
$A_2B_2C_2$, длины сторон которого равны длинам медиан треугольника$A_1B_1C_1$, подобен треугольнику$ABC$. - Найдите площадь треугольника
$A_2B_2C_2$, если площадь треугольника$ABC$ равна$S$.
Задача 9. Пусть точка
Задача 10. В прямоугольном треугольнике
Задача 11. Докажите неравенство $$ \underbrace{\sqrt[3]{6+\sqrt[3]{6+\ldots\sqrt[3]{6+\sqrt[3]6}}}}_n+ \underbrace{\sqrt{6+\sqrt{6+\ldots\sqrt{6+\sqrt6}}}}_m\lt5. $$
Задача 12. Докажите, что для всякого треугольника
$\cos\widehat A+\cos\widehat B+\cos\widehat C\le\dfrac32$; $\cos2\widehat A+\cos2\widehat B+\cos2\widehat C\ge-\dfrac32$.
Задача 13. Найдите предел
Задача 14. Упростите выражение
$$
\dfrac{(x-a)(x-b)}{(c-a)(c-b)}+\dfrac{(x-a)(x-c)}{(b-a)(b-c)}+
\dfrac{(x-b)(x-c)}{(a-b)(a-c)},
$$
где
Задача 15. Упростите выражения
$\sin^3\alpha\cos3\alpha+\cos^3\alpha\sin3\alpha$; $\sin^2x+\sin^2\alpha+\sin^2(x+\alpha)+2\cos\alpha\cos x\cos(\alpha+x)$;
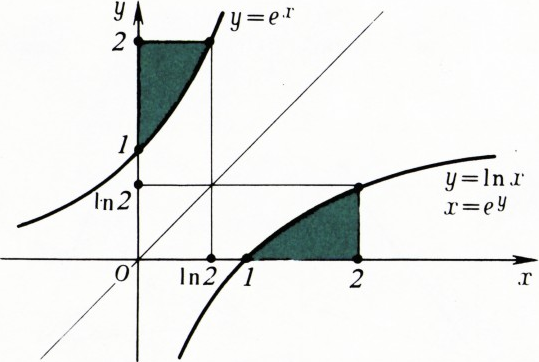
Задача 16. Найдите площадь фигуры, ограниченной линиями
Задача 17. Решите уравнение $$ x^3+1=2\sqrt[3]{2x-1}. $$
Ответы, указания, решения
- Из условия следует, что
$\dfrac58-\dfrac38=\dfrac14$ длины моста человек пробегает за время, в течение которого автомобиль проезжает всю длину моста. Следовательно, скорость человека равна$\dfrac14\cdot60=15~\text{км/ч}$. - Если предположить, что мяч покоится в пункте
$A$, вода неподвижна, а мост подплывает к мячу со скоростью течения реки, то спортсмен плывёт десять минут в одну сторону и столько же времени — обратно (вода неподвижна), «догоняя» мяч в пункте$A$ под мостом. Значит, мост «плыл» со скоростью$\dfrac{1000}{20}=50~\dfrac{\text{м}}{\text{мин}}$. Это и есть скорость течения реки. - Пусть первоначально в колбе было
$x$ % соли, т. е.$\frac x{100}=\dfrac XV$, где$X$ — масса соли, а$V$ — масса раствора. После указанных в задаче действий масса раствора станет равной$V-\dfrac Vn+\dfrac V{2n}$, a так как масса соли$X$ не изменится, мы получим $$ \dfrac{x+p}{100}=\dfrac X{V-\dfrac Vn+\dfrac V{2n}}=\dfrac XV\cdot \dfrac{2n}{2n-1}=\dfrac x{100}\cdot\dfrac{2n}{2n-1}, $$ откуда$x=p(2n-1)$. - Пусть прямоугольник
$OABC$ (рис. 1) изображает количество заданной работы.$OAED$ — количество работы, выполненной до подключения$x$ добавочных механизмов. Остальную работу, изображённую прямоугольником$CBED$, выполнили$27+x$ механизмов. Следовательно, второй период работ изобразится прямоугольником$DHGF$ ($|DH|=27+x$), равновеликим прямоугольнику$DEBC$, у которого$|DF|=(35-11)-6=18$, так как эта часть работы выполнена на 6 часов раньше срока. Далее, $$ \begin{gathered} S_{FKBC}=S_{EHGK},\\ 27\cdot6=18\cdot x,\\ x=9. \end{gathered} $$ - Если
$x$ — масса куска, отрезаемого от каждого из кусков сплава массы$m$, а$p$ и$q$ — процентные содержания меди в первом и втором кусках соответственно, то, как легко понять, $$ p(m-x)+qx=q(m-x)+px, $$ откуда$x=\dfrac m2$. - Каждый кусок сплава серебра и золота характеризуется двумя числами:
массой серебра
$x$ и массой всего куска$y$, т. е. вектором$(x;y)$. Когда мы сплавляем вместе два куска, соответствующие векторы, очевидно, складываются. Если$m_1$ и$m_2$ — искомые массы первого и второго сплава, то мы должны получить вектор$\left(8\cdot\dfrac{5}{11+5};8\right)=\left(\dfrac52;8\right)$, складывая векторы$\left(m_1\cdot\dfrac25;m_1\right)$, $\left(m_2\cdot\dfrac3{10};m_2\right)$, что приводит к системе $$ \left\{\begin{array}{l} m_1+m_2=8,\\[9pt] \dfrac{3m_2}{10}+\dfrac{2m_1}5=\dfrac52, \end{array}\right. $$ откуда$m_1=1$, $m_2=7$. - Поворотом
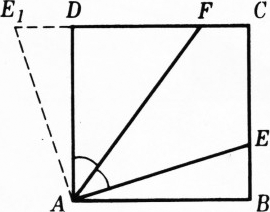
$\mathrm{R}_A^{90^\circ}$ отобразим$\triangle ABE$ на$\triangle ADE_1$ (рис. 2); из$\widehat{AFD}=\widehat{FAB}=\widehat{FAE_1}$ следует$|AE_1|=|EE_1|$. Из свойств поворота$|AE|=|AE_1|$ и$|BE|=|DE_1|$. Значит, $$|DF|+|BE|=|DF|+|DE_1|=|EE_1|=|AE_1|=|AE|=a.$$ - Пусть
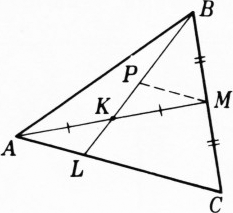
$AM$, $BN$ и$CP$ — медианы данного$\triangle ABC$ (рис. 3),$O$ — точка их пересечения. На продолжении$AM$ за точку$M$ возьмём точку$O'$ такую, что$|MO'|=|MO|$. Длины сторон треугольника$BOO'$ составляют по$\dfrac23$ длин медиан$\triangle ABC$. Легко видеть, что длины медиан треугольника$BOO'$ равны половинам длин сторон$\triangle ABC$. Поэтому в треугольнике, полученном из$\triangle BOO'$ подобием с коэффициентом$\dfrac32$, длины сторон будут равны длинам медиан$\triangle ABC$ (значит, это искомый$\triangle A_1B_1C_1$), а длины его медиан —$\dfrac34$ длин сторон$\triangle ABC$. - Значит, в треугольнике, полученном из
$\triangle ABC$ подобием с коэффициентом$\dfrac34$, длины сторон как раз будут равны длинам медиан$\triangle A_1B_1C_1$, т. е. этот треугольник и есть$\triangle A_2B_2C_2$. - По построению
$S_{\triangle A_2B_2C_2}=\dfrac9{16}S_{\triangle ABC}= \dfrac9{16}S$.
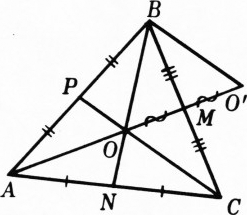
Рис. 3 Треугольник
$A_1B_1C_1$ можно построить также при помощи векторов:$\overrightarrow{AM}=\overrightarrow{AB}+\dfrac12\overrightarrow{BC}$, $\overrightarrow{BN}=\overrightarrow{BC}+\dfrac12\overrightarrow{CA}$, $\overrightarrow{CP}=\overrightarrow{CA}+\dfrac12\overrightarrow{AB}$; следовательно,$\overrightarrow{AM}+\overrightarrow{BN}+ \overrightarrow{CP}=\overrightarrow{0}$; значит, если от какой-нибудь точки$A_1$ отложить вектор$\overrightarrow{A_1B_1}=\overrightarrow{AM}$ и затем от точки$B_1$ отложить вектор$\overrightarrow{B_1C_1}=\overrightarrow{BN}$, получим$\overrightarrow{C_1A_1}=\overrightarrow{CP}$, причём, ввиду неколлинеарности векторов$\overrightarrow{AM}$, $\overrightarrow{BN}$, $\overrightarrow{CP}$, точки$A_1$, $B_1$, $C_1$ нe лежат на одной прямой; треугольник$A_1B_1C_1$ будет искомым.- Пусть
- Ясно, что
$S_{AMC}=\dfrac12$ (см. рис. 4). Для нахождения$S_{KLMC}$ достаточно найти площадь треугольника$AKL$ и вычесть её из$\dfrac12$. Проведём$[MP]\parallel(AC)$; $\triangle AKL$ очевидно, конгруэнтен$\triangle PMK$ и поэтому($PM$ — средняя линия в$\triangle BLC$) $|AL|=\dfrac13|AC|$. Значит,$S_{AKL}=S_{ALB}-S_{AKB}=\dfrac13-\dfrac14=\dfrac1{12}$, $S_{KLMC}=\dfrac12-\dfrac1{12}=\dfrac5{12}$. - Пусть
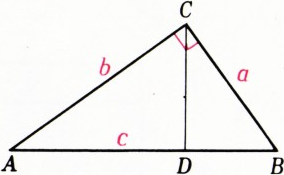
$P$ — периметр$\triangle ABC$. Поскольку$\triangle ACD\sim\triangle CBD\sim\triangle ABC$, их периметры относятся как сходственные стороны. Поэтому (см. рис. 5)$\dfrac b{P_1}=\dfrac a{P_2}=\dfrac cP$. Отсюда$\dfrac{P_1}P=\dfrac bc$, $\dfrac{P_2}P=\dfrac ac$. Возведя в квадрат полученные пропорции и складывая их, получим $$ \begin{gathered} \dfrac{P_1^2+P_2^2}{P^2}=\dfrac{a^2+b^2}{c^2}=1,\\ P=\sqrt{P_1^2+P_2^2}. \end{gathered} $$ - Заметим, что
$\sqrt[3]6\lt2$, a$\sqrt6\lt3$. Заменив теперь последний кубический корень в первом слагаемом на 2, а последний из квадратных корней второго слагаемого на 3, сразу получим требуемое. - Рассмотрим единичные векторы
$\overrightarrow{e_1}$, $\overrightarrow{e_2}$, $\overrightarrow{e_3}$, коллинеарные векторам$\overrightarrow{AB}$, $\overrightarrow{BC}$ и$\overrightarrow{CA}$ соответственно. Поскольку$(\overrightarrow{e_1}+\overrightarrow{e_2}+\overrightarrow{e_3})^2\ge0$, $$ \overrightarrow{e_1}^2+\overrightarrow{e_2}^2+\overrightarrow{e_3}^2+ 2\overrightarrow{e_1}\overrightarrow{e_2}+2\overrightarrow{e_2} \overrightarrow{e_3}+2\overrightarrow{e_1}\overrightarrow{e_3}=3+ 2\cos(\pi-B)+2\cos(\pi-C)+2\cos(\pi-A)\ge0, $$ откуда и следует нужное неравенство. - Указание. Воспользуйтесь неравенством
$(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})^2\gt0$, где$O$ — центр описанной окружности.
- Рассмотрим единичные векторы
- При
$n\gt3$ $$ 0\lt\dfrac{2^n}{n!}=\dfrac{2\cdot2\cdot2\cdot\ldots\cdot2}{1\cdot2\cdot3\cdot \ldots\cdot n}\le2\cdot\left(\dfrac23\right)^{n-2}. $$ Так как$\left(\dfrac23\right)^{n-2}\to0$, искомый предел существует и равен нулю. - Очевидно, функция, приведённая в условии, — многочлен степени не более
2. Поскольку
$f(a)=f(b)=f(c)=1$, то$f(x)=1$ при всех$x$. - Имеем:
$$
\begin{gather*}
F'(\alpha)=3\sin^2\alpha\cos3\alpha\cos\alpha-3\sin^3\alpha\sin3\alpha+
3\cos3\alpha\cos^3\alpha-3\cos^2\alpha\sin3\alpha\sin\alpha=\\
=3\sin^2\alpha\,(\cos3\alpha\cos\alpha-\sin3\alpha\sin\alpha)+3\cos^2\alpha\,
(\cos3\alpha\cos\alpha-\sin3\alpha\sin\alpha)=3\cos4\alpha.
\end{gather*}
$$
Поэтому
$F(\alpha)=\dfrac34\sin4\alpha+C$. Для нахождения$C$ зaметим, что$F(0)=0$. Значит,$C=0$ и$F(\alpha)=\dfrac34\sin4\alpha$. - Решая аналогично предыдущей задаче, получаем
$f(x)=2$.
- Имеем:
$$
\begin{gather*}
F'(\alpha)=3\sin^2\alpha\cos3\alpha\cos\alpha-3\sin^3\alpha\sin3\alpha+
3\cos3\alpha\cos^3\alpha-3\cos^2\alpha\sin3\alpha\sin\alpha=\\
=3\sin^2\alpha\,(\cos3\alpha\cos\alpha-\sin3\alpha\sin\alpha)+3\cos^2\alpha\,
(\cos3\alpha\cos\alpha-\sin3\alpha\sin\alpha)=3\cos4\alpha.
\end{gather*}
$$
Поэтому
- Чтобы найти искомую площадь, надо либо проделать симметрию около прямой
$y=x$ (рис. 6), либо рассматривать криволинейную трапецию «над осью ординат» (тогда её будет ограничивать кривая$x=e^y$). Вычитая из площади прямоугольника$2\ln2$ площадь криволинейной трапеции:$\int\limits_0^{\ln2}e^x\,dx$ (при первом способе) или$\int\limits_0^{\ln2}e^y\,dy$ (при втором способе), получаем ответ$2\ln2-1$. - Запишем уравнение, равносильное исходному:
$$
x=\sqrt[3]{2\sqrt[3]{2x-1}-1}.
$$
Пусть
$f(x)=\sqrt[3]{2x-1}$. Наше уравнение имеет вид$x=f(f(x))$. Докажем, что оно равносильно уравнению$x=f(x)$. Ясно, что всякий корень второго уравнения удовлетворяет исходному. Если же$x_0$ — корень уравнения$x=f(f(x))$, но$f(x_0)\ne x_0$, то либо$f(x_0)\gt x_0$, либо$f(x_0)\lt x_0$. Поскольку$f$ возрастает, в первом случае получаем$x_0=f(f(x_0))\gt f(x_0)$, во втором$f(x_0)\gt f(f(x_0))=x_0$ — противоречие. Решая уравнение$x^3=2x-1$ или$x^3-2x+1=(x-1)(x^2+x-1)=0$, получаем ответ$\left\{1,\dfrac{-1\pm\sqrt5}2\right\}$.