Изображения страниц
Текст статьи Задачи // Квант. — 1981. — № 12. — С. 37.

- В равенствах
$$
\begin{gather*}
a:b=c,\\
c+d=e,\\
e-f=g,\\
g\cdot h=10i+j
\end{gather*}
$$
расставьте вместо букв 10 цифр 0, 1,
$\ldots$, 9 так, чтобы получились верные равенства. - В коврике, сплетённом из разноцветных верёвок (см. рисунок), есть верёвочное кольцо, при разрезании которого коврик распадается на три части так, что две из этих частей состоят из одинакового числа верёвок, а третья — всего из одной верёвки. Укажите это кольцо.
- Докажите, что в любом выпуклом семиугольнике есть две диагонали, угол
между которыми меньше
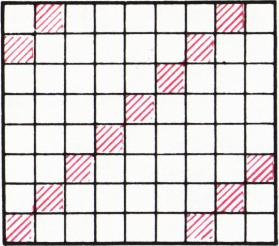
$13^\circ$. - Толя предложил Ире разрезать «клетчатый» прямоугольник размером
$8\times9$ (см. рисунок) по линиям сетки на прямоугольные полоски$1\times6$. Сможет ли Ира это сделать? - В первой строчке записаны три целых числа:
$a$, $b$, $c$. Во второй строчке под ними записаны три разности:$a-b$, $b-c$, $c-a$. Числа в третьей строчке образованы из чисел второй строчки по тому же закону и т. д. Покажите, что ни в одной из строчек ниже седьмой не может встретиться число 279.
Эти задачи нам предложили
Ф. Бартенев, А. Калинин, А. Савин,
А. Швецов.
Ответы, указания, решения
$a=6$, $b=3$, $c=2$, $d=7$, $e=9$, $f=1$, $g=8$, $h=5$, $i=4$, $j=0$. - Нужно разрезать любое жёлтое кольцо. Тогда коврик распадается на жёлтое кольцо и два зацепления, которые математики называют кольцами Борромео (см. «Квант», 1980, № 7 и 1981, № 9).
Количество диагоналей выпуклого семиугольника равно 14 (докажите!). Если какие-то две диагонали параллельны, то угол между ними
$0^\circ$, что меньше$13^\circ$. Пусть теперь не так.Выберем на плоскости некоторую точку
$O$ и проведём через неё 14 прямых, параллельных диагоналям семиугольника. Эти прямые разобьют плоскость на 28 углов, в сумме составляющих$360^\circ$. Предположим, что каждый из этих углов не меньше, чем$13^\circ$, тогда их сумма будет не меньше$28\cdot13^\circ=364^\circ$, a на самом деле она равна$360^\circ$. Противоречие!- Не сможет. Допустим противное. Заштрихуем некоторые квадраты
сетки (см. рисунок). При вырезании любой прямоугольной полоски
$1\times6$ в неё попадёт одна и только одна заштрихованная клетка. Из большого прямоугольника должно получиться 12 прямоугольных полосок$1\times6$. Но эти полоски будут содержать 12 заштрихованных клеток, а таких клеток 13. Противоречие. - В восьмой строчке будут записаны числа
$27(b-a)$, $27(c-b)$, $27(a-c)$. Следовательно, числа восьмой строчки и все последующие числа должны делиться на 27. Число же 279 на 27 не делится.