Изображения страниц
Текст статьи Задачи // Квант. — 1981. — № 11. — С. 31.
- В клетки таблицы
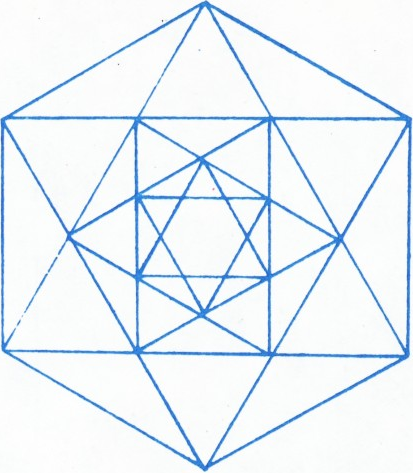
$n\times n$ записаны числа$-1$, 0 и 1. Может ли быть так, чтобы суммы чисел по строкам, столбцам и большим диагоналям были все различны? - Сколько треугольников содержит фигура, изображённая на рисунке?
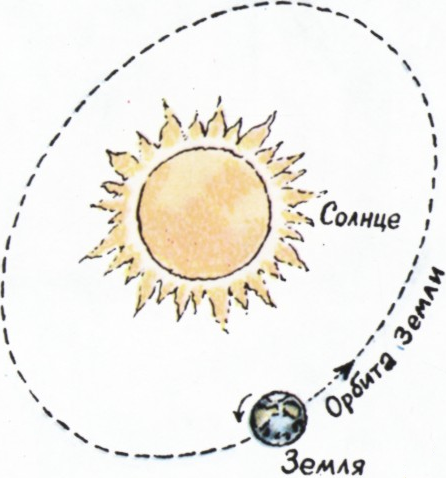
- Сколько оборотов совершает Земля вокруг своей оси за один год? (Продолжительность года считать равной 365 дням.)
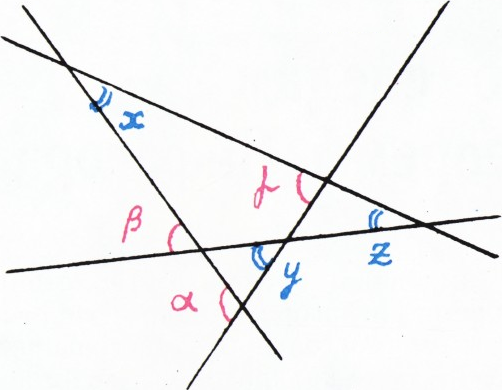
- На плоскости расположены четыре прямые (см. рисунок). Известны углы между
некоторыми из них:
$\alpha=110^\circ$, $\beta=60^\circ$, $\gamma=80^\circ$. Найдите углы между остальными парами прямых. - Найдите все такие двузначные числа, которые делятся на произведение своих цифр.
- На пакете с фотоплёнкой написано: «Обрабатывать при красном свете». Получится ли на этой плёнке пиратский флаг, изображённый на рисунке слева? А флаг, изображённый справа?

Эти задачи нам предложили
Т. Волощик, ученица 7 класса школы № 3 г. Белоозёрска,
Ф. Бартенев,
Г. Коткин,
Б. Мукушев,
А. Савин.
Ответы, указания, решения
- Не может. В самом деле, всего получается
$2n+2$ сумм, которые могут принимать только$2n+1$ разных значений:$-n$, $-n+1$, $\ldots$, $-1$, 0, 1,$\ldots$, $n-1$, $n$. - 120 треугольников.
- 366 оборотов.
$y=\alpha-\beta=50^\circ$, $z=\gamma-y=30^\circ$, $x=\beta-z=30^\circ$. Пусть
$n=10a+b=kab$. Тогда$b=la$ $\Rightarrow$ $10a+la=kla^2$ $\Rightarrow$ $10+l=kla$, т. е. 10 делится на$l$; значит,$l\in\{1,2,5\}$: $l=1$ $\Rightarrow$ $11=ka$, $k=11$, $a=1$, $b=1$, $n=1$. $l=2$ $\Rightarrow$ $12=2ka$ $\Rightarrow$ $6=ka$. $k=1$, $a=6$, $b=12$ — не может быть;$k=2$, $a=3$, $b=6$, $n=36$; $k=3$, $a=2$, $b=4$, $n=24$; $k=6$, $a=1$, $b=2$, $n=12$.
$l=5$ $\Rightarrow$ $15=5ka$ $\Rightarrow$ $3=ka$. $k=1$, $a=3$, $b=15$ — не может быть;$k=3$, $a=1$, $b=5$, $n=15$.
Ответ:
$n=11$, 12, 15, 24, 36.- Фотоплёнка реагирует на красный свет так же, как на темноту, т. е. «не отличает» красного от чёрного. Поэтому красный череп на белом флаге получится чёрным (на позитиве), а череп на чёрном флаге на снимке виден не будет.
