Рубинов Р.

По следам теоремы ПифагораРубинов Р. По следам теоремы Пифагора // Квант. — 1981. — № 11. — С. 32‍—‍35.‍‍

В нынешнем учебнике геометрии теорема Пифагора «Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов» доказывается «алгебраически», выкладкой («Геометрия 6‍—‍8», п. 67).

Евклид доказывал её «геометрически». Он строил на сторонах прямоугольного треугольника квадраты и доказывал, что сумма площадей квадратов на катетах равна площади квадрата на гипотенузе. Сейчас мы приведём два доказательства теоремы Пифагора, использующие эту идею, а затем предъявим много других фигур, для которых выполнено то же «пифагорово соотношение», что и для квадратов.

Строим квадраты

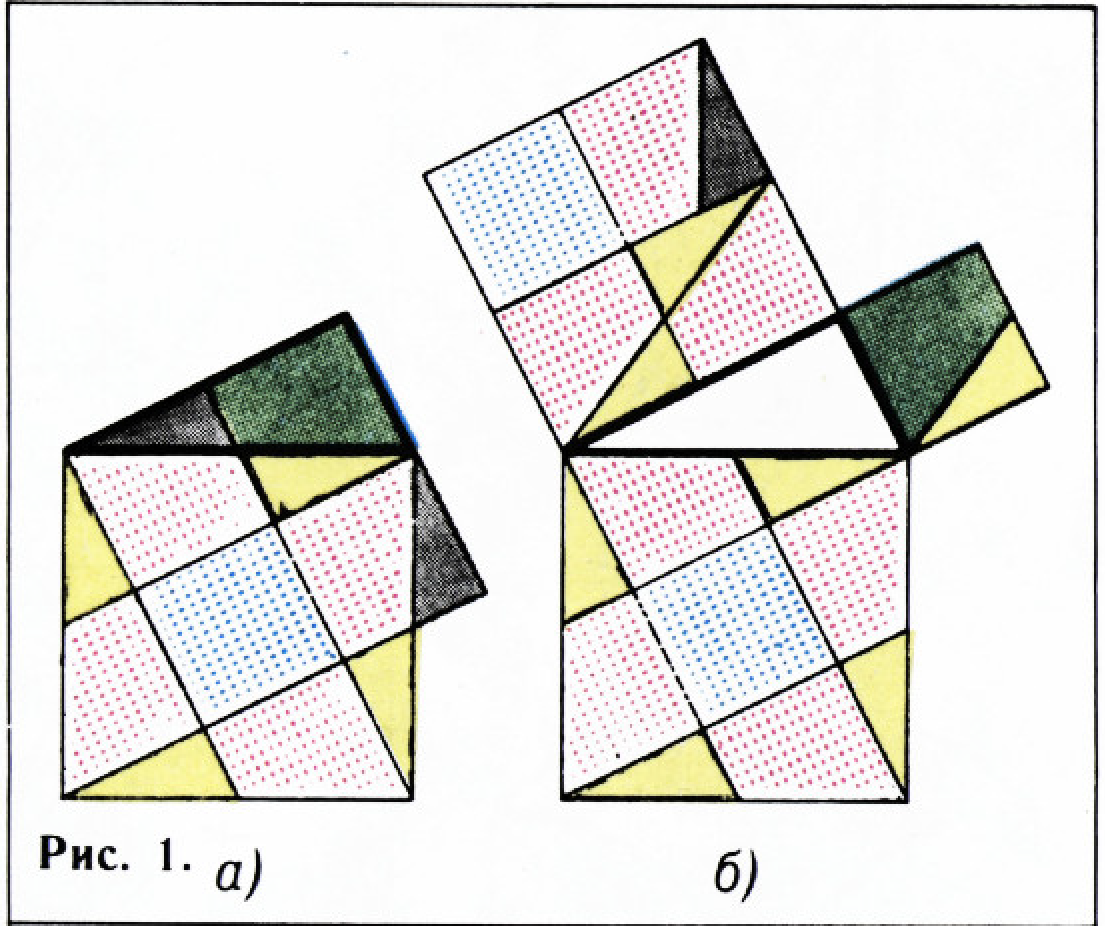
На рисунке 1, а на катетах выделенного прямоугольного треугольника внутрь построены квадраты; квадрат на гипотенузе построен наружу. Везде, где один квадрат налегает на другой, стороны квадратов продолжены. Равновеликие фигуры‍ окрашены в одинаковый цвет. Из рисунка видно, что треугольник, образованный из красной трапеции и жёлтого треугольника («красно-жёлтый» треугольник), равновелик треугольнику, образованному из зелёной трапеции и серого треугольника («серо-зелёный» треугольник). На рисунке 1, б на катетах исходного треугольника (теперь белого) квадраты построены внешним образом, причём в одном из них серо-зелёный треугольник заменён на равновеликий ему красно-жёлтый. Заменив ещё раз зелёную трапецию с серым треугольником на красную трапецию с жёлтым треугольником, получим нужное равенство площадей.

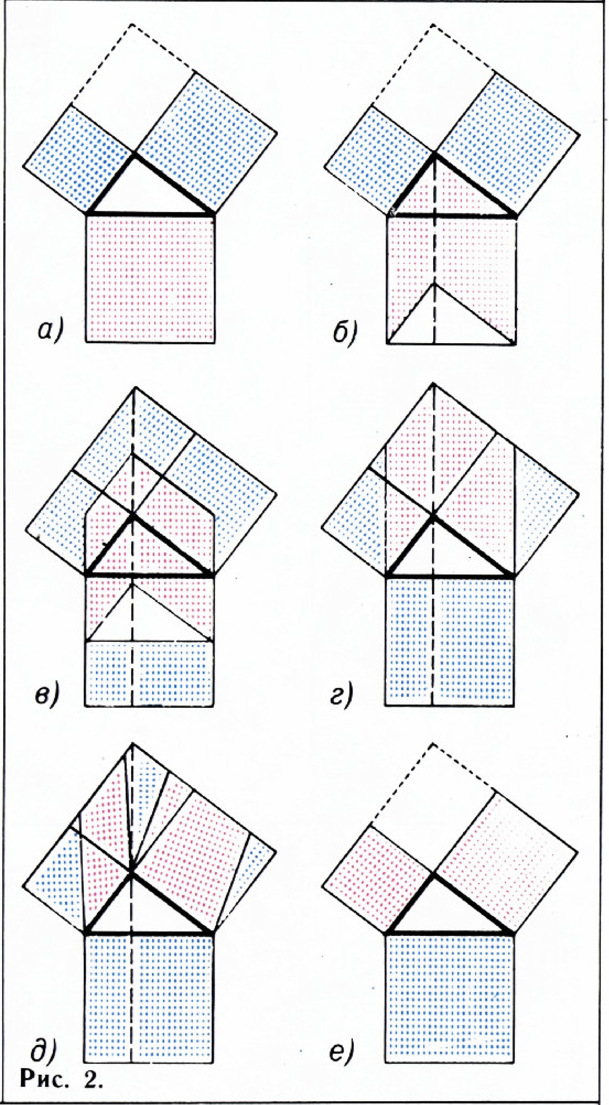
Ещё одно доказательство получается из рисунков 2, а‍—‍е; оно использует тот факт, что синяя высота в нашем прямоугольном треугольнике (см. заставку) и красная диагональ прямоугольника, образованного продолжениями сторон квадратов, лежат на одной прямой (докажите это!).

Обобщаем теорему Пифагора

Итак, в прямоугольном треугольнике $$ a^2+b^2=c^2, $$ где $a$‍,‍ $b$‍,‍ $c$‍‍ — его катеты и гипотенуза. Заметим теперь, что если у нас есть фигуры $A$‍,‍ $B$‍‍ и $C$‍,‍ площади $S_A$‍,‍ $S_B$‍‍ и $S_C$‍‍ которых равны, соответственно, $ka^2$‍,‍ $kb^2$‍‍ и $kc^2$‍,‍ то $S_A+S_B=S_C$‍.‍ В частности, «пифагорово соотношение» выполняется для площадей подобных фигур, построенных на сторонах прямоугольного треугольника‍ (Это замечание может пригодиться для вычисления площадей фигур, которые мы будем рисовать ниже.)

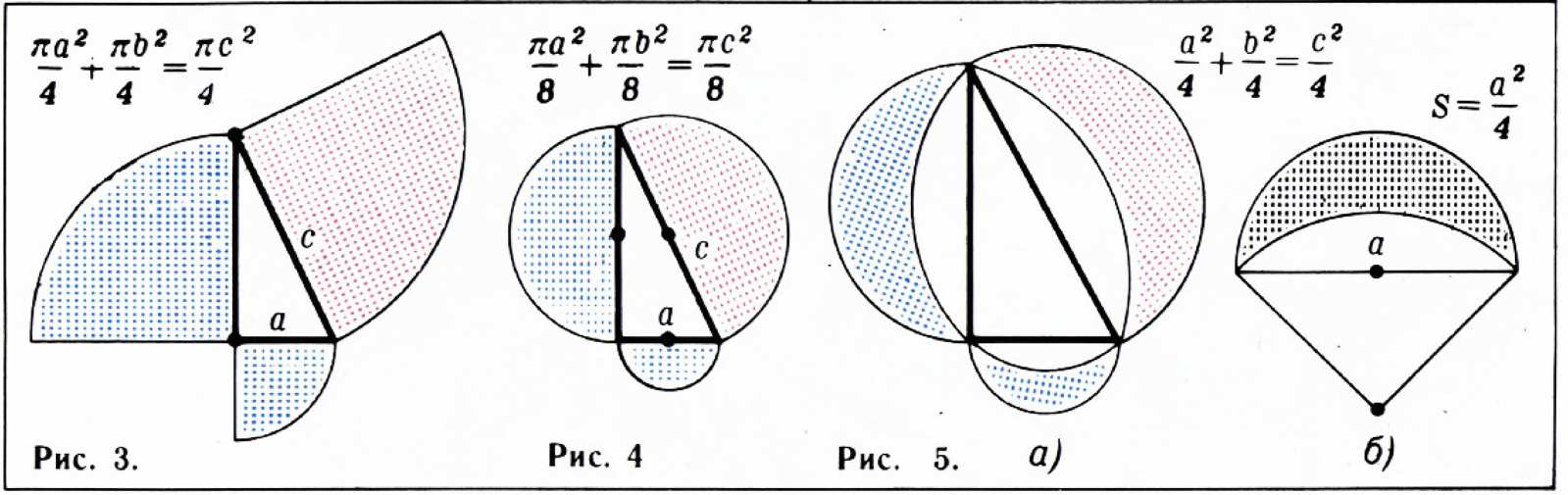
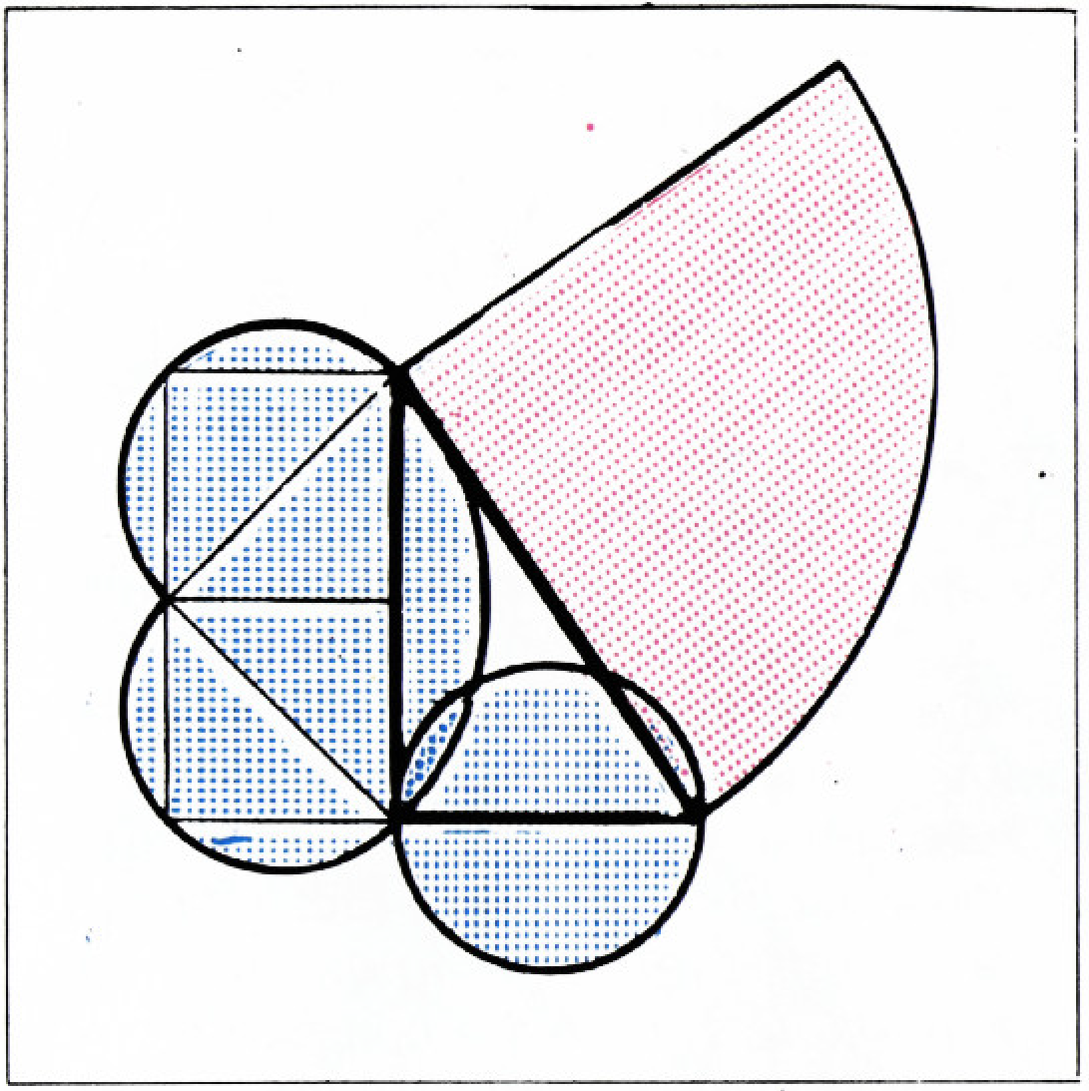
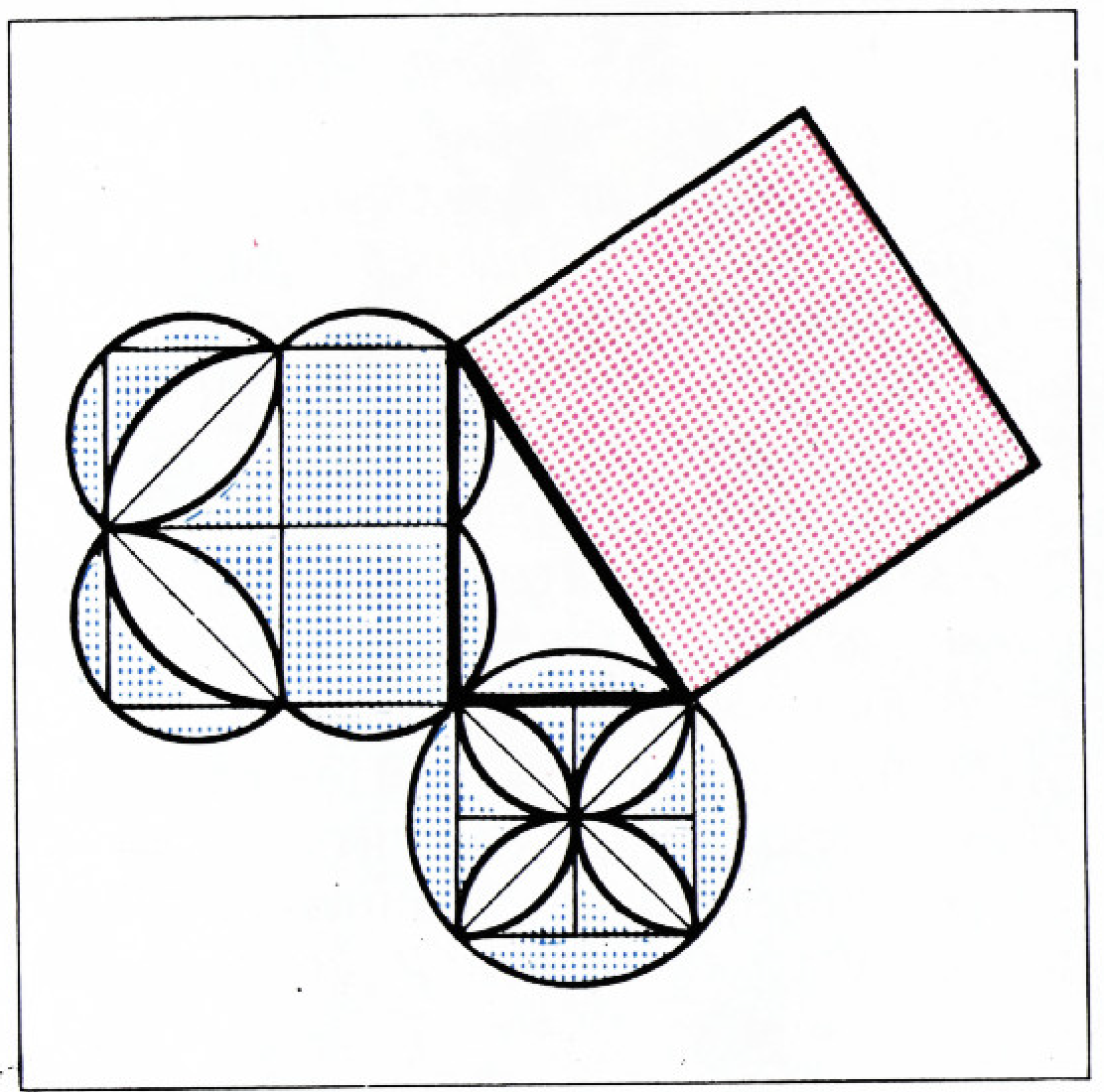
На сторонах прямоугольного треугольника мы будем теперь строить секторы (рис. 3), полукруги (рис. 4), луночки (рис. 5), дуговые треугольники (рис. 6).

Комбинируя секторы и круги, луночки и дуговые треугольники, мы получим рисунки 7 и 8: на них снова сумма площадей синих фигур равна площади красной фигуры.

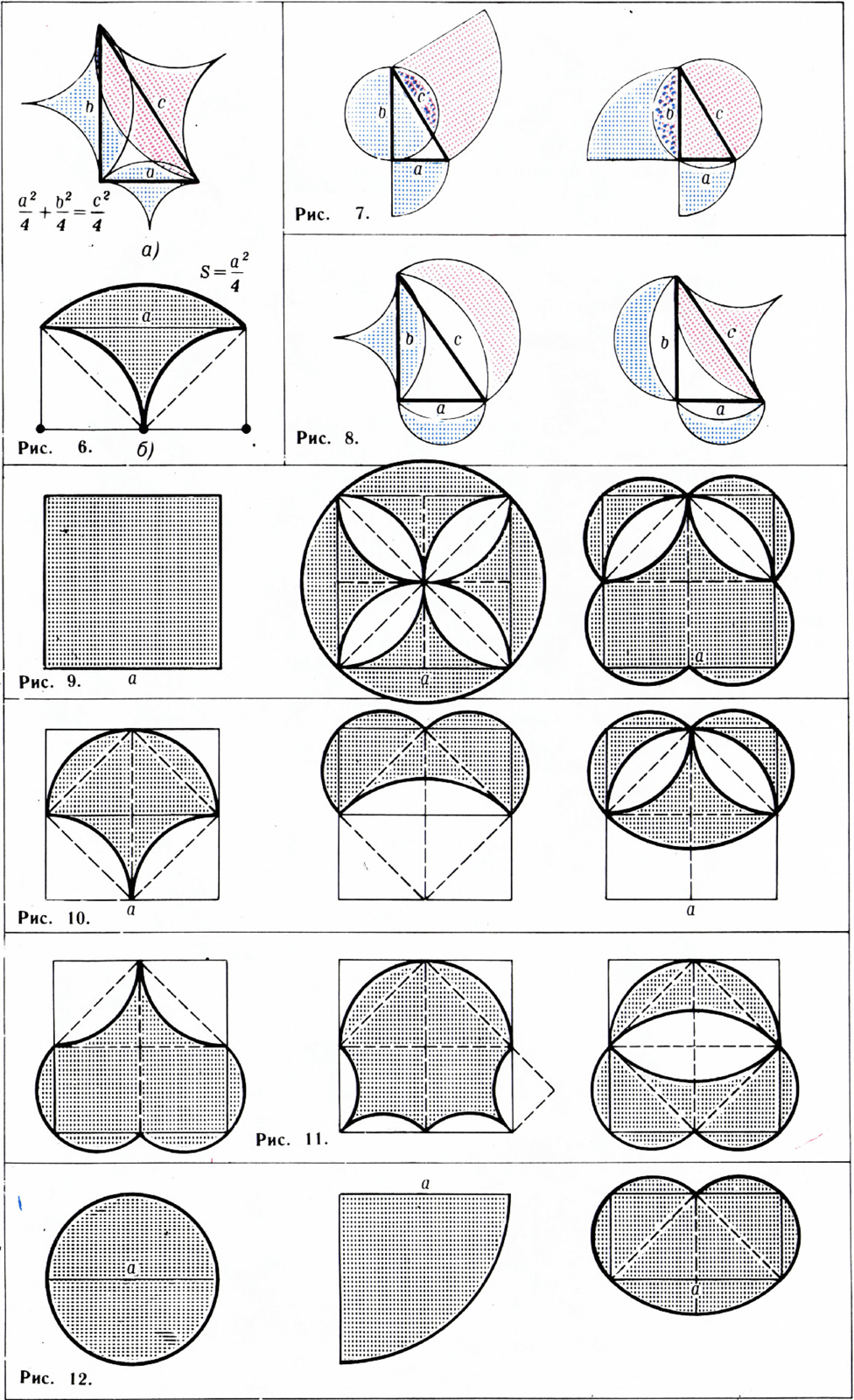
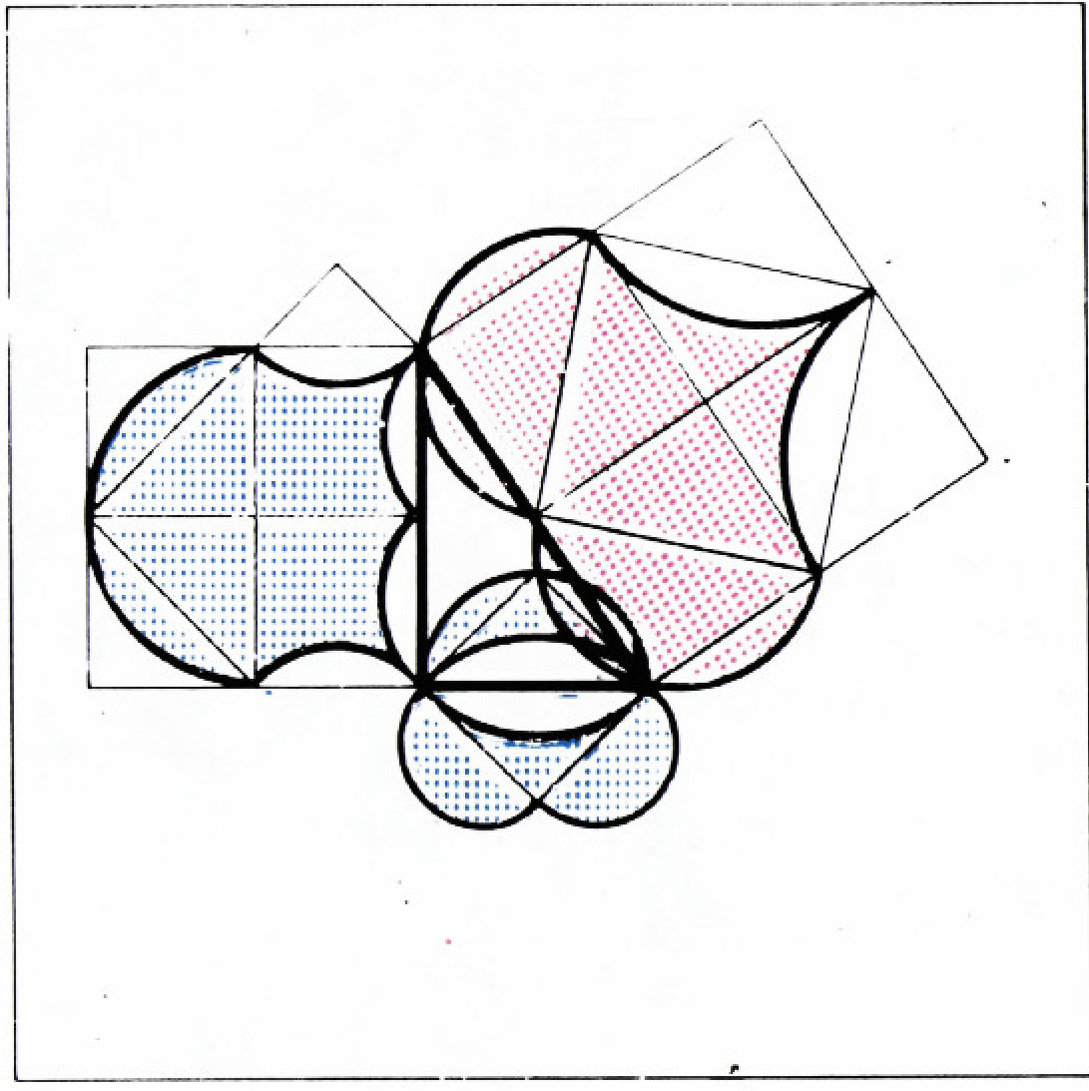
На рисунках 9‍—‍12 изображено по три равновеликие фигуры: на рисунке 9 — площади $a^2$‍‍ ($a$‍‍ — сторона квадрата), на рисунке 10 — площади $\dfrac{a^2}2$‍,‍ на рисунке 11 — площади $\dfrac{3a^2}4$‍,‍ на рисунке 12 — площади $\dfrac{\pi a^2}4$‍‍ (проверьте это!). Комбинируя их на катетах и гипотенузе прумоугольного треугольника, получим серию рисунков 13‍—‍16.

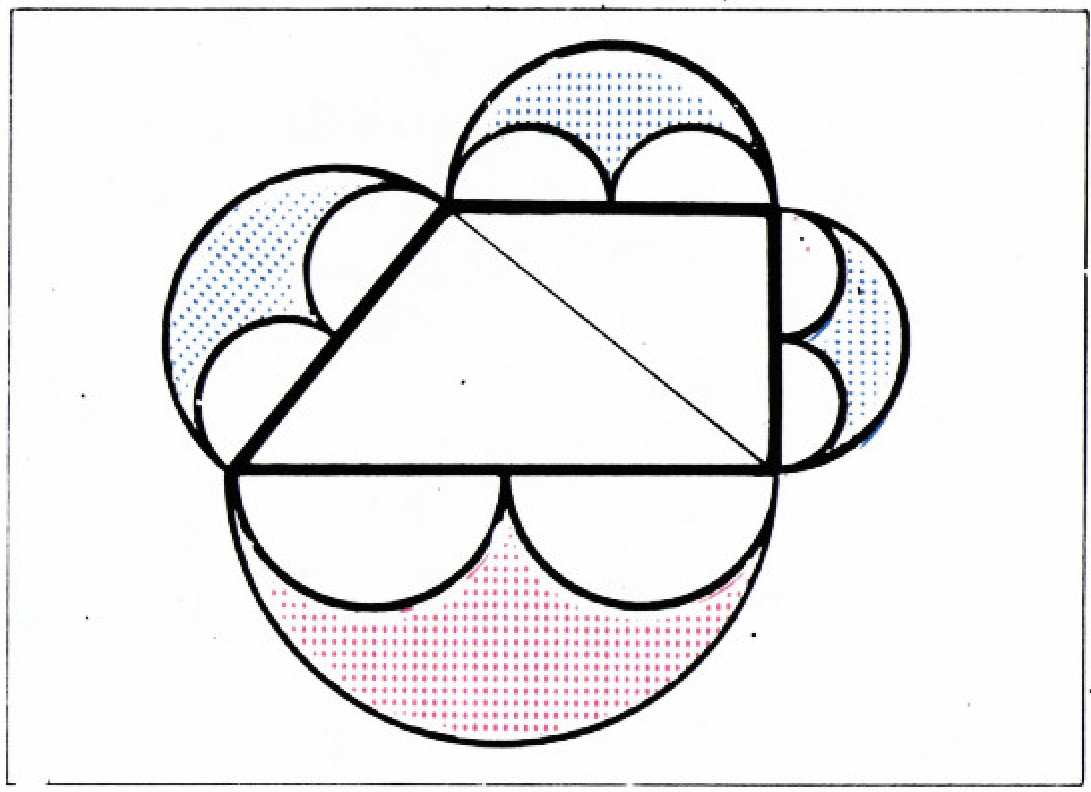
В заключение мы предлагаем вам доказать, что сумма площадей трёх синих криволинейных треугольников, построенных на сторонах прямоугольной трапеции, диагональ которой перпендикулярна боковой стороне (рис. 17), равна площади такого же треугольника, построенного на большем основании. Теперь вам понадобится для этого не более двух минут!