Изображения страниц
Текст статьи Задачи // Квант. — 1981. — № 10. — С. 41.
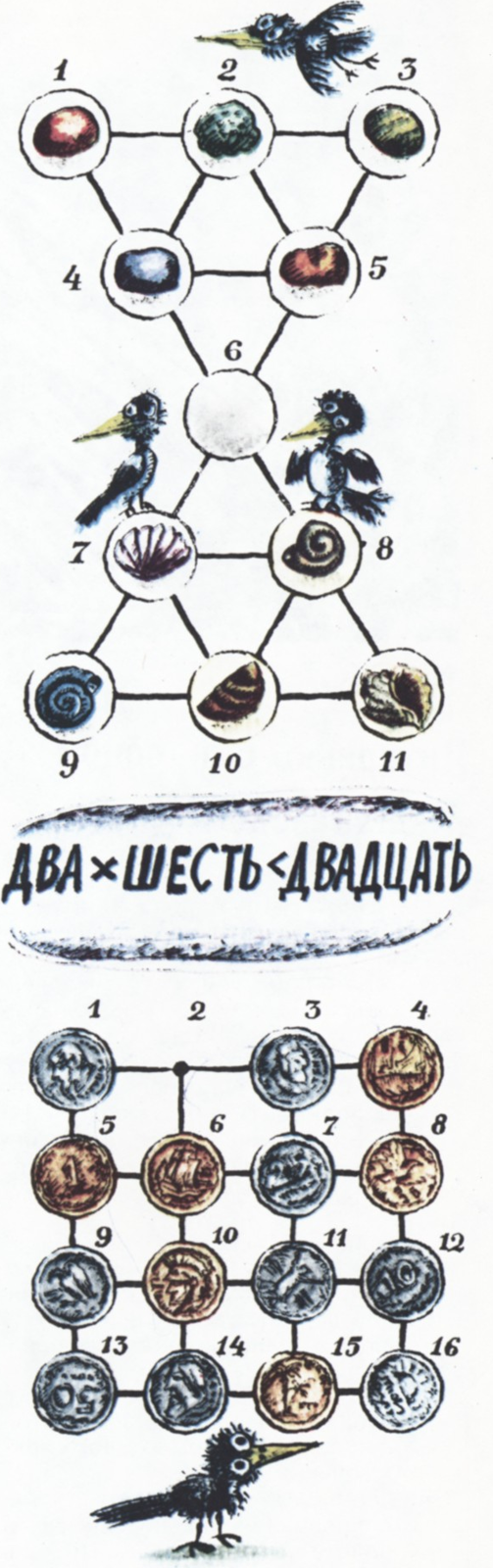
- В кружочках с номерами 1, 2,
$\ldots$, 5 (см. рисунок) находятся камушки (по одному в каждом кружочке); в кружочках с номерами 7, 8,$\ldots$, 11 — ракушки (также по одной в каждом кружочке). Камушкам и ракушкам разрешается перемещаться вдоль линий на соседний свободный кружочек и перепрыгивать (вдоль линий) через любого соседа на свободный кружочек (вначале свободен кружочек с номером 6). Можно ли добиться того, чтобы камушки и ракушки поменялись местами? - Докажите неравенство $$\text{ДВА}\times\text{ШЕСТЬ}\lt\text{ДВАДЦАТЬ}.$$ (Здесь каждая буква обозначает цифру, причём разным буквам соответствуют разные цифры, одинаковым — одинаковые.)
- 15 монет расположены в узлах клетчатой бумаги так, как показано на рисунке (в узле № 2 монеты нет!). Монета может переместиться в свободный узел, перепрыгнув вдоль линий сетки через свою соседку, которая при этом удаляется. Можно ли, сделав 14 ходов, добиться того, чтобы осталась одна монета?
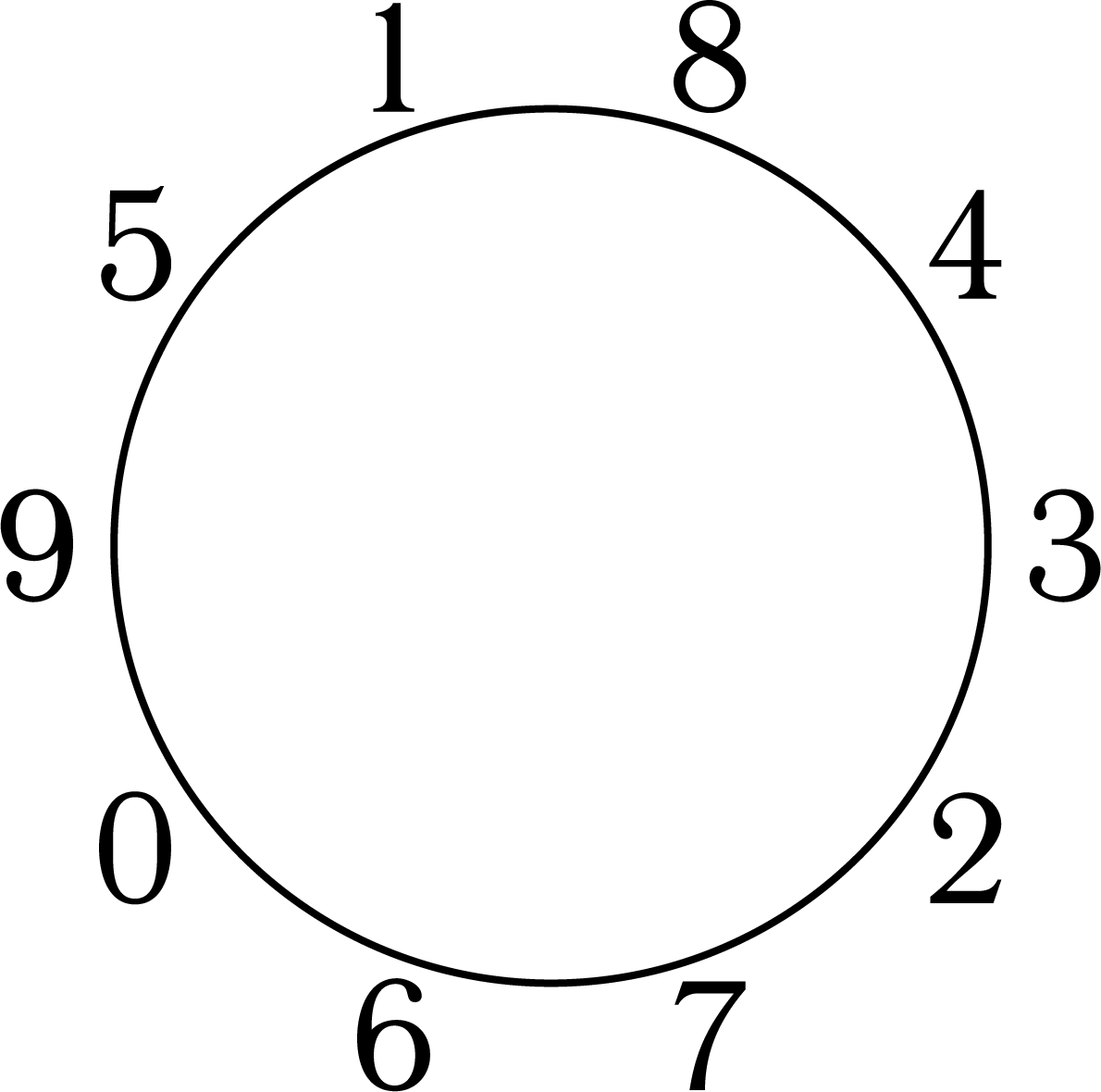
- Можно ли все десять цифр расставить по окружности так, чтобы сумма любых
трёх из них, идущих подряд, не превышала
- 13,
- 14,
- 15?
- Существует ли целое число, произведение цифр которого равно 528?
Эти задачи нам предложили
Ф. Бартенев и А. Савин.
Ответы, указания, решения
- Можно. Нужно последовательно ходить на свободный кружочек
с кружочков с номерами
$5$, $7$, $6$, $4$, $2$, $5$, $4$, $8$, $6$, $9$, $7$, $5$, $3$, $6$, $11$, $10$, $7$, $5$, $4$, $1$, $6$, $11$, $8$, $4$, $6$. $\text{ДВА}\times\text{ШЕСТЬ}$ меньше, а$\text{ДВАДЦАТЬ}$ больше, чем$\text{ДВА}\times 100\,000$. - Можно. Одно из возможных решений:
$10\to2$; $12\to10$; $14\to6$; $2\to10$; $16\to14$; $8\to6$; $5\to7$; $13\to5$; $14\to6$; $3\to11$; $5\to7$; $11\to3$; $4\to2$; $1\to3$. - Нельзя. Если бы это можно было сделать, то сумма всех десяти сумм не превосходила бы 130, но сумма всех цифр равна 45, а в нашу «сумму сумм» каждая цифра входит три раза.
- Нельзя. Действительно, цифры 3 и 6, 9 и 7, 9 и 8 не могут быть в одной тройке. Поэтому среди ближайших четырёх соседей девятки (двух — с одной, и двух — с другой стороны) нет цифр 6, 7, 8. Значит, среди них есть 4 или 5 (поскольку цифры 8, 7, 6, 5, 4 не могут идти подряд), так что среди них есть также 0 или 1. Но тогда невозможно расставить цифры 8, 6 и 7 (убедитесь в этом!).
- Можно (см. рисунок).
- Такого числа нет, поскольку 528 делится на 11.