Изображения страниц
Текст статьи Задачи наших читателей // Квант. — 1980. — № 1. — С. 55.
-
Назовём число (день) месяца «правильным», если остаток от его деления нa 7 совпадает с номером дня недели (воскресенье — нулевой день, понедельник — первый и т. д.). Назовём неделю «правильной», если все её дни «правильные». Какой ближайший в будущем год содержит
- максимальное число «правильных» дней;
- максимальное число «правильных» недель?
-
Докажите, что в арифметической прогрессии
$$ 1,\quad14,\quad27,\quad40,\quad\ldots $$бесконечно много членов, записываемых одними двойками. Найдите общий вид этих членов.
-
Докажите, что в последовательности
$$ 31,\quad331,\quad3331,\quad33331,\quad\ldots $$найдётся бесконечно много членов, делящихся на 31, и ни одного, делящегося на 13.
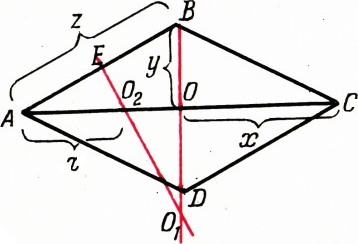
Найдите площадь ромба
$ABCD$, если радиусы окружностей, описанных, соответственно, около треугольников$ABC$ и$ABD$ равны$R$ и$r$. В некотором царстве
$3n!$ городов и$n$ видов транспорта($n!=1\cdot2\cdot\ldots\cdot n$; читается: «эн-факториал»). Любые два города связаны между собой только одним видом транспорта. Докажите, что всегда найдётся такой город, выехав из которого можно побывать не менее чем в двух городах и вернуться обратно, не меняя вида транспорта.
Ответы, указания, решения
$b_n=2\cdot\dfrac{10^{6n-3}-1}9$, $n=1$, 2, 3,$\ldots$ -
Имеем:
$$ \dfrac z{2r}=\dfrac xz,\quad \dfrac z{2R}=\dfrac yz. $$$S=2xy$ (обозначения см. на рисунке). Найдём произведение$xy$. Построим$[O_1E]\perp[AB]$, где$|AE|=|EB|$ (рис.). Тогда по условию$|O_1B|=R$, $|O_2A|=r$ ($O_2=[AO]\cap[O_1E]$). Треугольники$AO_2E$, $O_1BE$ и$BOC$ подобны, поэтомуОтсюда
$$ z^2=\dfrac{4r^2R^2}{R^2+r^2},\quad xy=\dfrac{z^4}{4rR}, $$т. е.
$$ S=\dfrac{8r^3R^3}{(R^2+r^2)^2}. $$ -
Доказательство проведём методом математической индукции. Для
$$ (3k!-1)\cdot(k+1)=3(k+1)!-k-1\lt3(k+1)!-1, $$$n=1$ утверждение задачи очевидно. Предположим, что оно верно для некоторого$n=k$. Докажем, что тогда оно верно для$n=k+1$. Пусть имеется$3(k+1)!$ городов, для связи между которыми используется$k+1$ видов транспорта. Возьмём некоторый город$C$. Он связан с$3(k+1)!-1$ городами. Докажем, что найдётся не менее$3k!$ городов, с которыми город$C$ связан одинаковыми видами транспорта. Предположим противное: пусть таких городов менее$3k!$, т. е. не более$3k!-1$. Так как всех видов транспорта$k+1$, то город$C$ будет соединён не более чем с$(3k!-1)\cdot(k+1)$ городами. Hoтак как
$k\ge1$. Получили противоречие, поскольку знаем, что город$C$ соединён с$3(k+1)!-1$ городами.Итак, найдётся не менее чем
$3k!$ городов, с которыми город$C$ связан одинаковыми видами транспорта. Предположим, что среди этих$3k!$ городов имеются города$A$ и$B$, связанные между собой тем же видом транспорта, что и с городом$C$. Значит, выехав из города$C$, мы, не меняя вида транспорта, побываем в городах$A$ и$B$ и вернёмся обратно в$C$. Если же двух таких городов не найдётся, то придём к случаю, когда имеется$3k!$ городов и$k$ видов транспорта, что даёт утвердительный ответ на вопрос задачи по предположению индукции.
