Изображения страниц
Текст статьи Головоломки наших читателей // Квант. — 1979. — № 1. — С. 64.
В кружках данной фигуры (рис. 1) расставьте 13 последовательно идущих чисел так, чтобы все шесть сумм четырёх чисел, расположенных в вершинах ромбов, были бы одинаковы и равнялись бы 1977. Известно, что одно из этих чисел равно 496, и что оно стоит в центральном кружочке.
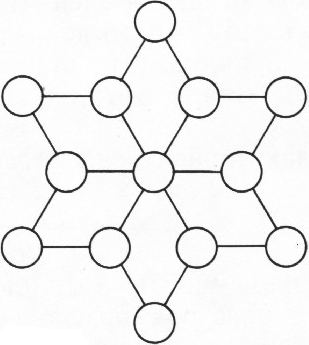
Рис. 1 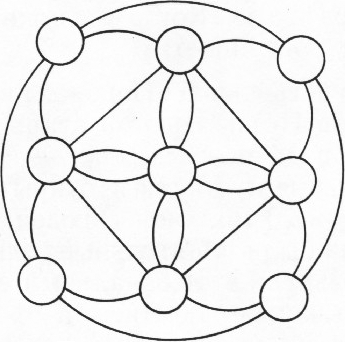
Рис. 2 В кружочках изображённой на рисунке 2 фигуры расставьте девять последовательных натуральных чисел так, чтобы суммы чисел по большой и по четырём малым окружностям, а также в вершинах выделенного центрального квадрата были бы одинаковы и равнялись шестидесяти.
Ответы, указания, решения
Наименьшее число равно 488, наибольшее — 500. Один из возможных способов расстановки этих чисел показан на рисунке 11.
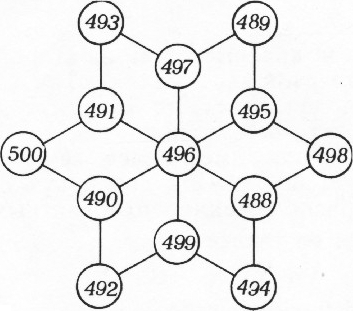
Рис. 11 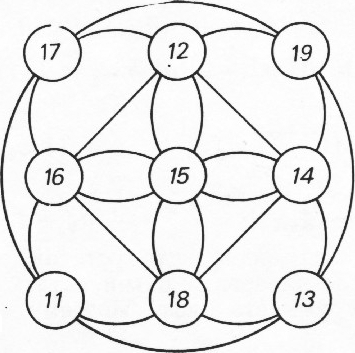
Рис. 12 Наименьшее расставляемое число равно 11, наибольшее — 19; способ расстановки чисел показан на рисунке 12.




