Изображения страниц
Текст статьи Задачи // Квант. — 1977. — № 1. — С. 40.


В чемпионате мира среди профессионалов по крестикам-ноликам на бесконечной клетчатой доске участвовало 10 игроков. Проигравший партию, потеряв надежду на главный приз, уезжал с чемпионата. Какое максимальное число участников могло выиграть по две партии? (В «крестиках-ноликах» на бесконечной доске выигрывает тот, кто поставит пять своих значков подряд по одной линии — вертикали, горизонтали или диагонали; ничьих не бывает.)
Когда одного любителя головоломок спросили, отчего он так успешно решает задачи, то в ответ было написано $$ \text{Н}:\text{Е}=0{,}\text{СТАРЕЮСТАРЕЮСТАРЕЮ}\ldots $$ Попробуйте расшифровать эту запись.
В этом примере на умножение (см. рисунок) одинаковыми буквами зашифрованы одинаковые цифры, разными — разные, вместо звёздочек могут стоять любые цифры. Расшифруйте пример.
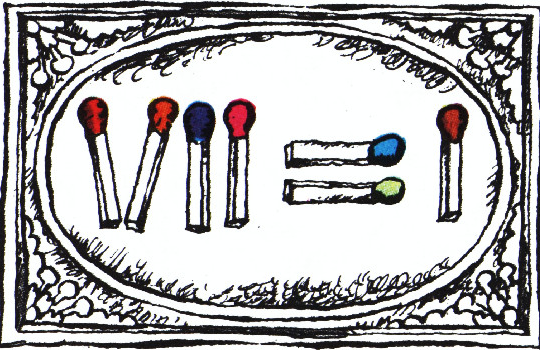
В неверном равенстве из спичек (см. рисунок) переложить одну спичку так, чтобы оно превратилось в верное.
Ответы, указания, решения
- Каждая партия кончается отъездом одного из игроков, поэтому чемпион
определяется ровно за 9 партий. Поскольку
$5\cdot2=10\gt9$, по две партии могли выиграть максимум четверо участников. Пример: Первый выиграл у Второго и Третьего, затем Четвёртый — у Первого и Пятого, Шестой — у Четвёртого и Седьмого, Восьмой — у Шестого и Девятого, Десятый — у Восьмого. $\text{Н}=3$, $\text{Е}=7$. $142\,857\cdot516\,342=73\,763\,069\,094$. $\sqrt1=1$.
