Изображения страниц
Текст статьи Задачи // Квант. — 1976. — № 4. — С. 52.

На шахматной доске на поле f8 стоит ферзь. Двое по очереди передвигают ферзя либо на несколько клеток вниз, либо на несколько клеток влево, либо на несколько клеток влево — вниз по диагонали. Выигрывает тот, кто загонит ферзя в левый нижний угол — на поле a1. Известно, что в этой игре начинающий, если он играет правильно, всегда выигрывает, как бы хорошо ни играл его партнёр. Как же должен играть начинающий, чтобы выиграть? Сколько ходов ему понадобится?
А кто выигрывает при правильной игре — начинающий или его противник, если вначале ферзь стоит на поле e8?
На дачном участке летом стояла палатка. Когда начались морозы, палатку сняли, а участок решили перекопать. Оказалось, что сухая земля непосредственно под палаткой успела промёрзнуть сильнее, чем окружающая более влажная земля. Как это объяснить?
В классе 35 учеников. Из них 20 занимаются в математическом кружке, 11 — в кружке «умелые руки», 10 ребят не ходят в эти кружки. Сколько «математиков» занимаются в «умелых руках»?
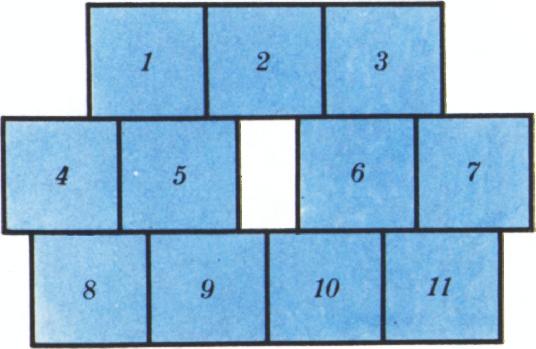
Расположите на плоскости одиннадцать одинаковых квадратов, не налегающих друг на друга, так, чтобы выполнялось следующее условие: как бы ни покрасить эти квадраты тремя красками, обязательно какие-нибудь два квадрата одного цвета будут иметь общий участок границы.
Ответы, указания, решения
- Начинающий должен двигать ферзя в проигрышные поля, их семь: a1, b3, c2, d6, e8, f4, h5. Из любого другого поля доски можно передвинуть ферзя в одно из этих полей, а из одного проигрышного поля попасть в другое нельзя (потому они и проигрышные). Находятся эти поля так: a1 — проигрышное; любое поле, с которого можно за один ход попасть в a1, — выигрышное; поля b3 и c2, с которых можно попасть только в уже отмеченные выигрышные, — проигрышные; любое поле, с которого можно попасть в b3 или c2, — выигрышное и т. д. Число ходов определите самостоятельно.
- Почва на участке была влажная, а на том месте, где стояла палатка, почва была сухая. При замерзании воды в почве выделялось тепло, которое «обогревало» влажные участки и замедляло их промерзание. А сухой участок под палаткой промёрз сильнее.
- Весь класс разбивается на 4 непересекающихся множества: «чистых
математиков», «математиков-умельцев», «чистых умельцев» и «бездельников».
«Бездельников» по условию 10, не «бездельников»
$35-10=25$, среди них 20 математиков, поэтому «чистых умельцев» будет$25-20=5$, а «математиков-умельцев» будет$11-5=6$. См. рисунок.