Изображения страниц
Текст статьи Задачи // Квант. — 1976. — № 1. — С. 73.
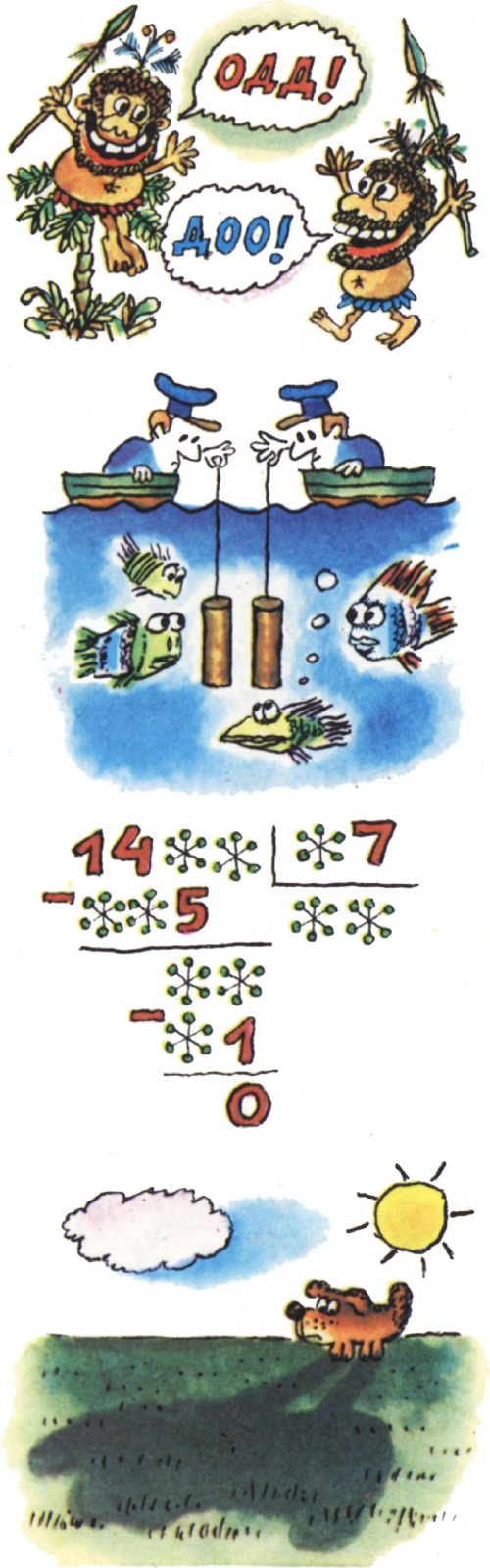
В языке племени ододо всего два звука: «Д» и «О». Два слова означают одно и то же, если одно получается из другого при помощи некоторого количества следующих операций: пропуска идущих подряд звуков ДО или ООДД и добавления в любое место сочетания ОД. Означают ли слова ОДД и ДОО одно и то же?
Две медные трубки опускают в воду на большую глубину. Одна трубка запаяна с обоих концов, а у другой — один конец открыт. Что произойдёт с трубками на глубине?
Восстановите запись деления, в которой некоторые «сбежавшие» цифры заменены звёздочками.
Известно, что длина тени, которую отбрасывает предмет, в течение дня меняется. Самая короткая тень — в полдень, к вечеру тень «растёт». А есть ли на Земле такое место, где длина тени в течение дня не меняется?
В игре «Кто первым назовёт число 100» участвуют двое. Один называет любое целое число от 1 до 9 включительно. Второй прибавляет к названному любое целое число от 1 до 9, которое ему понравится, и называет сумму. К этой сумме первый снова добавляет любое целое число от 1 до 9 и называет новую сумму и т. д. Выигрывает тот, кто первым назовёт число 100. В этой игре начинающий всегда проигрывает, если только его противник откроет один секрет. В чём же секрет, ключ игры, который обеспечивает второму игроку победу?
Ответы, указания, решения
- Нет. Указание. Изменения в словах не меняют разности между числом букв О и числом букв Д.
- На большой глубине трубка с запаянными концами будет сплющена силами давления воды. Открытая трубка деформироваться не будет.
$1431:27=53$. - На полюсе в течение суток высота Солнца над горизонтом почти не меняется. Поэтому тень от какого-нибудь предмета в течение суток «ходит по кругу», оставаясь всё время одной длины.
- Второй игрок должен называть число, дополняющее до 10 число, названное
первым игроком
($1+9=10$, $2+8=10$, $\ldots$, $9+1=10$).
