Изображения страниц
Текст статьи Задачи наших читателей // Квант. — 1975. — № 9. — С. 29.
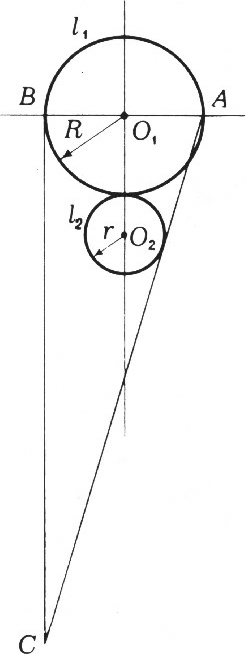
На рисунке вы видите две касающиеся окружности
$l_1$ и$l_2$ радиусов$R$ и$r=\dfrac R2$ соответственно;$AB\perp O_1O_2$, $BC$ — касательная к окружности$l_1$, $AC$ — касательная к окружности$l_2$. Доказать, что длина отрезка
$BC$ равна длине окружности$l_1$ с относительной ошибкой менее 0,005.Дана парабола — график функции
$y=x^2$. На оси$Oy$ взята точка$A$. Найти кратчайшее расстояние от точки$A$ до параболы.Можно пользоваться таким определением: парабола — это множество точек, равноудалённых от некоторой точки
$F$ и некоторой прямой$l$. Доказать, что числа вида
$7^{2n+1}+2^{2n+1}+5$, $7^{2n+1}+2^{2n+1}-5$, где$n$ — натуральное, нельзя представить в виде суммы трёх кубов натуральных чисел.
Ответы, указания, решения
- Провести окружность с центром в точке
$F$ и радиусом$|AF|$. Пусть она пересекает параболу в точке$K$, тогда отрезок$KA$ — искомый (для случая, когда эта окружность не пересекает параболу, ответ найдите самостоятельно). - Указание. Воспользуйтесь признаком делимости на 9.
