Изображения страниц
Текст статьи Задачи // Квант. — 1975. — № 8. — С. 58.

В ста ящиках было по одинаковому количеству деталей. Когда из первого ящика взяли несколько деталей, из второго в два раза больше, из третьего в три раза больше и так далее, то в последнем ящике осталась одна деталь, а во всех ста вместе —
$14\,950$. Сколько деталей было в каждом ящике первоначально?Как известно, моря? всё время пополняются пресной водой рек. Однако солёность морской воды при этом не уменьшается. Почему?
Король обошёл шахматную доску размером
$4\times4$ и вернулся на исходное поле, побывав на каждом поле один раз.Какое наименьшее число прямых (не диагональных) ходов он мог сделать?
Вместо букв на рисунке надо подобрать цифры (одинаковым буквам соответствуют одинаковые цифры), чтобы выполнялись все указанные соотношения.
Вася на вопрос, каков номер его квартиры, ответил так: «Если все шесть двузначных чисел, которые можно образовать из цифр номера, сложить, то половина полученной суммы составит как раз номер моей квapтиры.
В какой квартире живёт Вася?
Ответы, указания, решения
301 деталь. Общее число взятых деталей можно найти как сумму арифметической прогрессии, а именно, если из первого ящика взяли
$x$ деталей, то из всех вместе их взяли $$ x+2x+3x+\ldots+100x=5050x. $$ В последнем ящике было$100x+1$ деталей, во всех вместе$10\,000x+100$. Получаем уравнение $$ 10\,000x+100-5050x=14\,950, $$ откуда$x=3$. Вода с поверхности моря всё время испаряется, поэтому солёность морской воды не уменьшается.
-
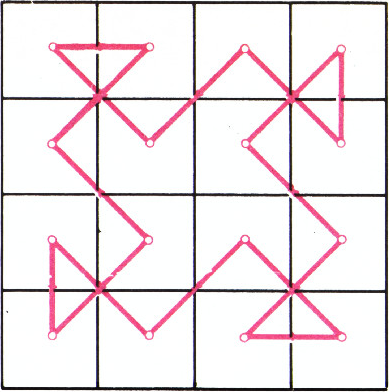
Четыре (см. рис.). Указание. В каждое угловое поле ведёт лишь один диагональный ход.
По строкам: $$ \colsep{0pt}{\begin{array}{rcrcr} 17&\enspace\times\enspace&28&\enspace=\enspace&476\\[-5pt] \mathllap{+}\quad&&\mathllap{\times}\quad&&\mathllap{-}\quad\\[-5pt] 99&+&9&=&108\\\hline 116&+&252&=&368 \end{array}} $$
Указание. Легко видеть, что
$\text{Я}=9$, $\text{Е}=1$, $\text{Д}=0$. Чтобы из цифр числа можно было составить шесть и только шесть двузначных чисел, необходимо, чтобы это число было трёхзначным:
$\overline{abc}$. Складывая$\overline{ab}$, $\overline{ac\vphantom b}$, $\overline{bc}$, $\overline{ba}$, $\overline{ca\vphantom b}$, $\overline{cb}$, получим$22(a+b+c)$. По условию$11(a+b+c)=100a+10b+c$, или$10c+b=89a$. Но$10c+b$ — число двузначное; значит, и$89a$ — число двузначное,$a=1$. Номер квартиры — 198.

