Арабаджи В. И.

Дифракционная окраска насекомыхАрабаджи В. И. Дифракционная окраска насекомых // Квант. — 1975. — № 2. — С. 18‍—‍19.‍‍

Дифракционная (структурная) окраска птиц, бабочек и жуков весьма распространена в природе. Большое разнообразие в оттенках дифракционных цветов свойственно павлинам, фазанам, чёрным аистам, колибри, бабочкам тропической зоны и многим видам жуков (среди них рогачи, долгоносики, листоеды и др.). Дифракционную окраску животных изучали не только биологи, но и физики, например Релей, Вуд, Майкельсон.

Внешняя поверхность оперения у многих птиц и верхний покров тела бабочек и жуков характеризуются регулярным повторением элементов структуры с периодом от одного до нескольких микрон. У некоторых животных подобные структуры могут покрывать тело в несколько слоёв, образуя многоэтажную (объёмную) дифракционную решётку.

Наряду с дифракционной животные могут иметь и чисто интерференционную окраску, образующуюся на тонких и прозрачных внешних покровах (клинообразных по сечению вдоль основной оси симметрии) с толщиной оптически деятельного слоя от десятых долей микрона до нескольких микрон.

На рисунках 1 и 2 вы видите снимки крыла бабочки-переливницы и спинки жука — азиатского листоеда (выбраны участки с дифракционной окраской). Снимки 1, 2, 3 получены с помощью микроскопа со стократным увеличением. Для выявления элементов структуры использовалось боковое освещение. На снимках чётко видно повторение элементов структуры.

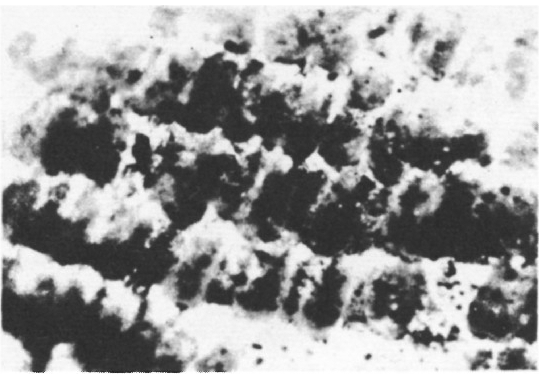
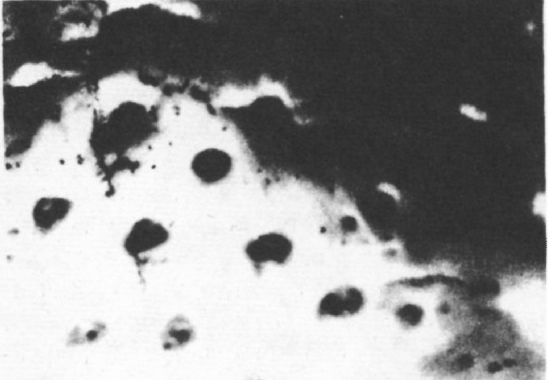
Цвет поверхностного покрова может изменяться в зависимости от того, под каким углом падает свет на поверхность решётки, как ориентированы лучи света по отношению к элементам структуры, под каким углом рассматривается поверхность.

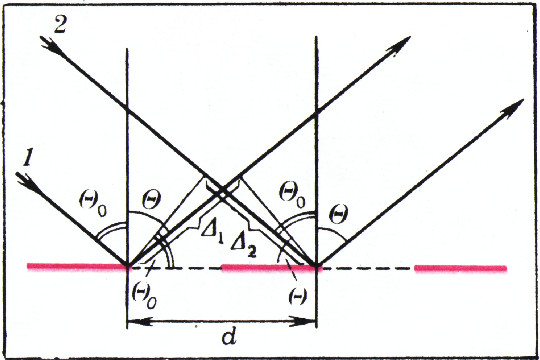
Очевидно, что окраска поверхности связана с отражением лучей. Рассмотрим количественно дифракцию в отражённом свете. Пусть лучи света падают на решётку под углом $\theta_0$‍,‍ и отражаются от неё под углом $\theta$‍‍ (рис. 4). Разность хода лучей 1 и 2 равна $$ \Delta=\Delta_2-\Delta_1=d\sin\theta_0-d\sin\theta,\tag1 $$ или $$ \Delta=2d\cos\dfrac{\theta_0+\theta}2\sin\dfrac{\theta_0-\theta}2.\tag2 $$

Поскольку для дифракционных максимумов $\Delta=k\lambda$‍‍ ($k=1$‍,‍ 2, $\ldots$‍),‍ то $$ k\lambda=2d\cos\dfrac{\theta_0+\theta}2\sin\dfrac{\theta_0-\theta}2.\tag3 $$

Наибольшая энергия локализована в первом дифракционном максимуме ($k=1$‍).‍ Для этого максимума, полагая, что $\theta$‍‍ близко к $\theta_0$‍,‍ из выражения (3) получим $$ \lambda=(\theta_0-\theta)d\cos\theta_0.\tag4 $$

Пусть $\theta_0=65^\circ$‍‍ (в рассматриваемом случае дифракция в отражённом свете наблюдается при наклонном падении лучей), а $\theta_0-\theta=3^\circ$‍‍ (примерно 0,05 рад). Тогда, например, для $d=2\cdot10^{-3}~\text{см}$‍‍ длина волны дифрагированного света из уравнения (4) равна $\lambda\approx0{,}4\cdot10^{-4}~\text{см}$‍.‍

Полученная величина $\lambda$‍‍ соответствует синей области спектра. Чаще всего дифракционная окраска в природе наблюдается в зелёном, синем или голубом свете. Из формулы (4) видно, что длина волны $\lambda$‍‍ зависит от угла падения света $\theta_0$‍.‍ Действительно, если освещать поверхность под разными углами, окраска может изменяться.

В случае многослойной дифракционной решётки условие образования дифракционных максимумов описывается уравнением $$ k\lambda=2l\cos\theta_0,\tag5 $$ где $l$‍‍ — расстояние между соседними слоями решётки. Это уравнение получается путём определения разности хода $\Delta=\Delta_1+\Delta_2$‍,‍ между лучами 1 и 2 (рис. 5) и замены $\Delta$‍‍ для дифракционных максимумов через $k\lambda$‍.‍

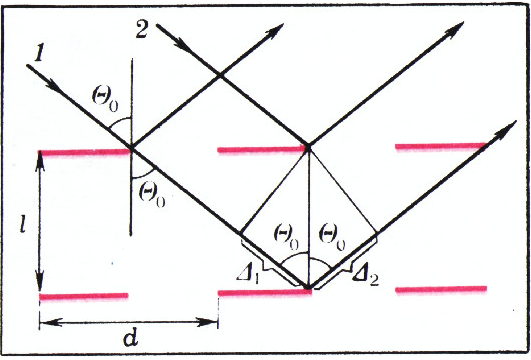
Полагая $k=1$‍,‍ из выражения (5) получим $$ \cos\theta_0=\dfrac{\lambda}{2l}.\tag6 $$ Отсюда следует, что дифракция на многослойной структуре возможна при $2l\gt\lambda$‍.‍