Изображения страниц
Текст статьи Задачи // Квант. — 1975. — № 12. — С. 67.
Мне и моей сестре сейчас вместе 26 лет, причём сестре в три раза меньше лет, чем мне будет тогда, когда нам вместе будет в пять раз больше лет, чем мне сейчас.
Сколько сейчас лет каждому из нас?
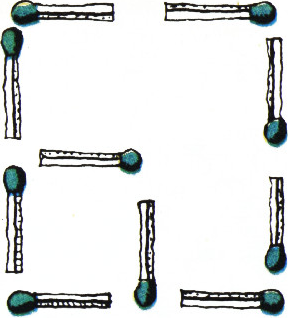
Из фигуры на рисунке удалите две спички так, чтобы осталось два квадрата.
Сколько надо взять слагаемых суммы $$ 1+2+3+4+5+\ldots, $$ чтобы получилось трёхзначное число, состоящее из одинаковых цифр?
Петя сказал Васе: «Задумай какое-нибудь трёхзначное число. Первую его цифру удвой. К полученному произведению прибавь три. Затем умножь полученную сумму на пять и прибавь к результату вторую цифру задуманного числа. Наконец, к полученной сумме припиши справа последнюю цифру задуманного числа. Сколько получилось? Пятьсот сорок? Ты задумал триста девяносто».
Как Петя узнал, какое число задумал Вася?
В примере (см. рисунок) цифры зашифрованы геометрическими фигурами. Расшифруйте пример.
Известно, что число
$a$ больше числа$b$ в$n$ раз, а сумма чисел$a$ и$b$ больше их разности в$m$ раз. Найти сумму чисел$m$ и$n$, если и$m$, и$n$ — натуральные числа.
Ответы, указания, решения
- Из таблицы
$$
\begin{array}{|c|c|c|}
\hline
&\text{сейчас}&\text{будет}\\\hline
\text{мне лет}&x&3(26-x)\\\hline
\text{сестре лет}&26-x&5x-3(26-x)\\\hline
\end{array}
$$
получаем уравнение
$$
x-(26-x)=3(26-x)-[5x-3(26-x)],
$$ откуда
$x=14$, $26-x=12$. См. рисунок.
- Из равенства
$$
\dfrac{n(n+1)}2=111\cdot k=3\cdot37\cdot k
$$
следует, что
$n=36$ или$n=37$. Подходит$n=36$, сумма равна 666. - Надо вычесть из результата 150. Разность — задуманное число.
$(11)^3=1331$. Указание.$\triangle\le3$ (при бо́льших значениях получится пятизначное число).- Из условия задачи следует, что
$\dfrac ab=n=1+\dfrac2{m-1}$. Тогда$n=3$ при$m=2$ и$n=2$ при$m=3$, в обоих случаях$m+n=5$.

