Изображения страниц
Текст статьи Задачи // Квант. — 1973. — № 6. — С. 74.
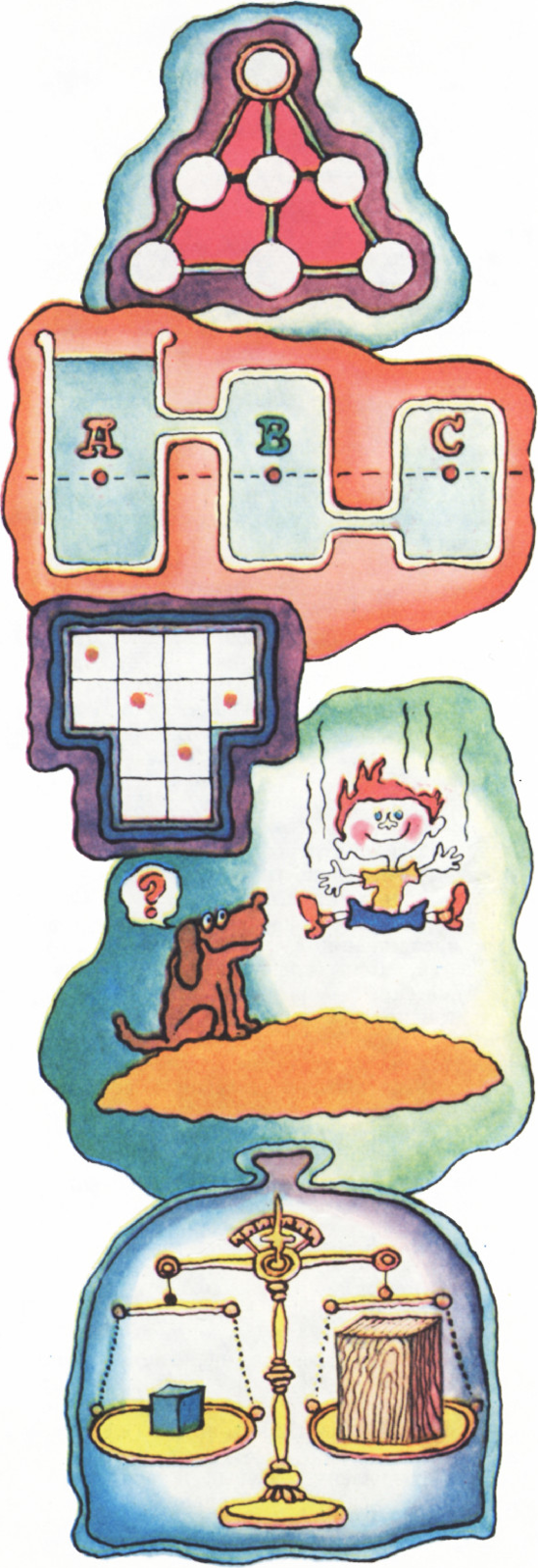
В кружках треугольника на рисунке справа были расставлены все числа от 1 до 7 (каждое по одному разу), причём сумма чисел вдоль каждого отрезка прямой была одна и та же.
Определите, какое число было записано в вершине треугольника и чему равнялись указанные суммы.
- В трёх сообщающихся сосудах находится вода. Левый сосуд открыт.
Одинаковое ли давление в точках
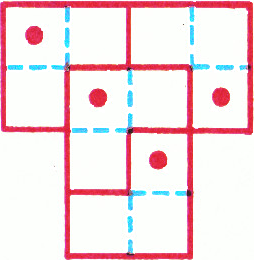
$A$, $B$ и$C$, если они лежат на одной горизонтали? - На рисунке справа изображена фигура в виде буквы Т с четырьмя отмеченными клетками. Разделите эту фигуру по линиям сетки на четыре одинаковые части, причём так, чтобы в каждой из частей было по одной отмеченной клетке.
- Прыгать с обрыва в песок безопаснее, чем на твёрдую землю. Почему?
- Как объяснить следующие равенства: $$ \begin{alignat*}{3} 09&{}={}&0&{}\times9+{}&(0&{}+9),\\ 19&{}={}&1&{}\times9+{}&(1&{}+9),\\ 29&{}={}&2&{}\times9+{}&(2&{}+9),\\ &&&\quad\mathclap{{\ldots}\,{\ldots}\,{\ldots}\,{\ldots}\,{\ldots}}\\ 99&{}={}&9&{}\times9+{}&(9&{}+9),\\ 109&{}={}&10&{}\times9+{}&(10&{}+9),\\ &&&\quad\mathclap{{\ldots}\,{\ldots}\,{\ldots}\,{\ldots}\,{\ldots}}\\ 1239&{}={}&123&{}\times9+{}&(123&{}+9) \end{alignat*} $$ и так далее?
- Деревянный и чугунный бруски по отдельности уравновешены в воздухе гирей 10 кг. Что произойдёт, если бруски положить на разные чашки весов, а весы поместить под стеклянный колпак и откачать воздух?
Ответы, указания, решения
- Четыре. Указание. Сложить числа на всех прямых; получится удвоенная сумма чисел от 1 до 7 плюс число в вершине. С другой стороны, эта сумма должна делиться на пять.
- Давления в точках
$A$, $B$ и$C$ различны. - См. рисунок.
- При прыжке в песок скорость гасится за более продолжительное время.
$10n+9=n\cdot9+(n+9)$. - В воздухе весы уравновешены. Если же воздух откачать, перевесит та чашка, на которой лежит деревянный брусок, так как по закону Архимеда в воздухе на него действовала бо́льшая выталкивающая сила.