Куперман Г. Б.

‍,

Щукин Е. Д.

Механические свойства кристалловКуперман Г. Б., Щукин Е. Д. Механические свойства кристаллов // Квант. — 1973. — № 10. — С. 37‍—‍41.‍‍

Такие свойства твёрдых тел как упругость, прочность, поверхностное натяжение определяются силами взаимодействия между атомами и строением кристаллов (типом кристаллической решётки). Изучая силы межатомного взаимодействия, можно, например, определить величину модуля упругости, предела прочности материала, энергии связи кристалла и коэффициента поверхностного натяжения.

Таким образом оцениваются характеристики любых твёрдых тел, но проще всего это сделать для идеальных ионных кристаллов. В решётке таких кристаллов периодически чередуются положительные и отрицательные ионы.

Для оценки прежде всего необходимо выяснить величину силы единичной межатомной связи, которая в ионных кристаллах определяется силой взаимодействия между двумя ионами.

Силы межатомного взаимодействия

Зависимость сил межатомного взаимодействия‍ от расстояния между центрами атомов в твёрдых телах схематически показана на рисунке 1.

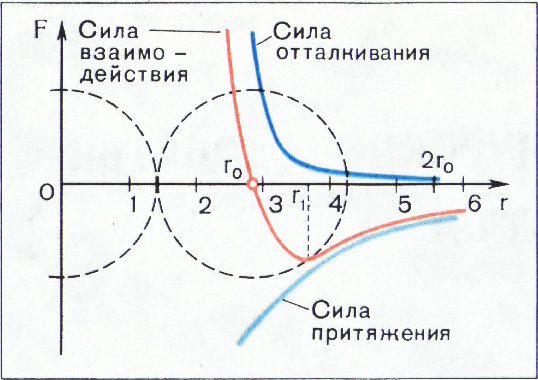
По этому рисунку можно судить о некоторых особенностях сил межатомного взаимодействия.

1. Между атомами одновременно действуют силы притяжения и силы отталкивания. Результирующая сила межатомного взаимодействия — сумма этих двух сил.
2. При уменьшении расстояния между атомами силы отталкивания нарастают значительно быстрее, чем силы притяжения; поэтому существует некоторое расстояние $r_0$‍,‍ при котором силы притяжения и силы отталкивания уравновешиваются и результирующая сила становится равной нулю. В кристалле, предоставленном самому себе, ионы располагаются именно на расстоянии $r_0$‍,‍ друг от друга. Если расстояние между атомами меньше равновесного ($r\lt r_0$‍),‍ то преобладают силы отталкивания, если ($r\gt r_0$‍),‍ то преобладают силы притяжения.

Эти свойства межатомных сил позволяют условно рассматривать частицы, образующие кристалл (например, ионы Na и Cl в кристалле поваренной соли), как твёрдые упругие шары, взаимодействующие друг с другом. Деформация растяжения кристалла приводит к увеличению расстояния между центрами соседних шаров и преобладанию сил притяжения, а деформация сжатия — к уменьшению этого расстояния и преобладанию сил отталкивания.

Прочность при растяжении

Пределом прочности обычно называют наибольшее напряжение‍, которое может выдержать материал, не разрушаясь. При растяжении образца предел прочности определяется максимальной величиной результирующей силы межатомного притяжения, приходящейся на единицу площади сечения, перпендикулярного направлению растяжения.

Результирующая сила межатомного взаимодействия достигает максимального значения, когда центры атомов находятся на расстоянии $r_1$‍‍ друг от друга (см. рис. 1). Когда растяжение ещё более увеличивается, силы взаимодействия становятся настолько малыми, что связи между атомами разрываются.

Обозначим величину наибольшей силы притяжения между двумя атомами (т. е. величину силы единичной связи) через $F_{\text{max}}$‍,‍ а число связей на единице площади сечения, перпендикулярного направлению внешней силы, через $N_{\text{св}}$‍.‍ Тогда предел прочности кристалла $$ \sigma=F_{\text{max}}\,N_{\text{св}}. $$

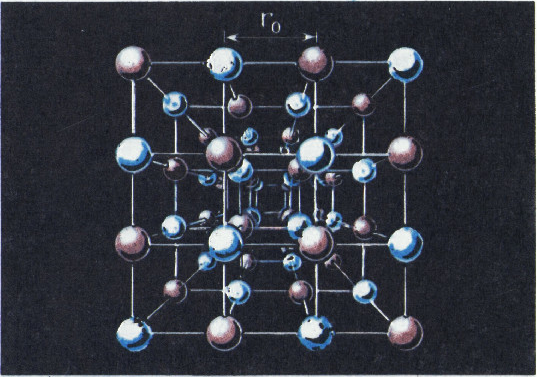
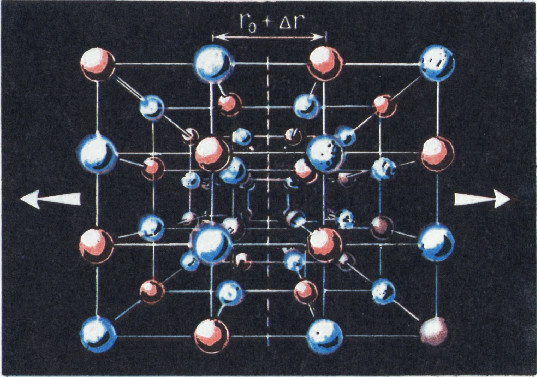
На рисунке 2 показана простейшая модель ионного кристалла поваренной соли (NaCl состоит из положительных ионов натрия и отрицательных ионов хлора). У каждого иона в этом кристалле шесть ближайших соседей с противоположным знаком заряда. При разрыве такого кристалла у каждого атома обрывается по одной связи. Разрыв кристалла схематически изображён на рисунке 3. В рассматриваемой модели число связей, разрываемых на каждом квадратном сантиметре, равно числу атомов, приходящихся на эту площадь ($N_{\text{св}}=N_{\text{ат}}$‍).‍ Для простоты мы пренебрегаем взаимодействием между ионами, находящимися друг от друга на расстояниях, больших $r_0$‍,‍ (остальные ионы удалены на расстояния не меньше, чем $r_0\sqrt2$‍).‍ Эти взаимодействия дают относительно небольшую поправку. Для оценки предела прочности о достаточно умножить наибольшее значение силы взаимодействия между двумя атомами на число атомов, приходящихся на единицу площади в плоскости разрыва: $$ \sigma = F_{\text{max}}\,N_{\text{ат}}. $$

Оценка величины сил связи

Порядок величины сил связи в ионных кристаллах можно найти, исходя из предположения, что ионы взаимодействуют по закону Кулона. В нашей модели кристалл состоит из чередующихся ионов противоположных знаков, равновесные расстояния между которыми $r_0\approx3~\text{Å}$‍‍‍. Предположим, что деформация остаётся упругой вплоть до деформации, соответствующей разрыву; иначе говоря, наибольшей упругой деформации соответствует напряжение, равное пределу прочности. Но максимальной упругой деформации приблизительно соответствует максимальное значение силы межатомного притяжения (см. рис. 1).

Опыты с самыми прочными кристаллами показали, что их максимальная относительная упругая деформация $\eps_{\text{max}}$‍‍‍ перед разрушением обычно не превышает 10‍—‍20%. Положим $\eps_{\text{max}}=\dfrac16\approx17\%$‍.‍ Этой относительной деформации соответствует смещение атомов от положения равновесия на расстояние $\Delta r=\eps r_0=\dfrac16\cdot3~\text{Å}=0{,}5~\text{Å}$‍.‍ Таким образом, при подсчёте сил межатомного притяжения для рассматриваемой модели кристалла за расстояние между ионами следует брать величину $$ r=r_0+\Delta r=3~\text{Å}+0{,}5~\text{Å}=3{,}5~\text{Å}. $$

Если учесть, что заряд каждого иона по величине равен заряду электрона, т. е. $q=1{,}6\cdot10^{-19}~\text{Кл}$‍,‍ то максимальное значение силы притяжения между двумя атомами будет равно $$ F_{\text{max}}=\dfrac1{4\pi\eps_0}\,\dfrac{q^2}{r^2}=9\cdot10^9\dfrac{(1{,}6\cdot10^{-19})^2}{(3{,}5\cdot10^{-10})^2}\approx2\cdot10^{-9}~(\text{Н}). $$ Таково по порядку величины значение единичной силы межатомной связи.

Прочность кристалла

Оценим примерное число атомов, приходящихся на единицу поверхности разрыва кристалла.

Диаметр иона равен приблизительно расстоянию между соседними ионами. Мы считали это расстояние равным 3 Å, тогда число атомов на каждом квадратном метре поверхности разрыва кристалла $$ N_{\text{ат}}\sim\dfrac1{(3\cdot10^{-10})^2}\approx10^{19}~{\left(\dfrac1{\text{м}^2}\right)}. $$

В нашей модели кристалла число связей, проходящих через единицу площади, равно числу атомов ($N_{\text{св}}=N_{\text{ат}}$‍),‍ значит, $N_{\text{св}}\approx10^{19}~\text{м}^{-2}$‍.‍

Теперь можно оценить теоретическую величину предела прочности кристаллов: $$ \sigma\approx2\cdot10^{10}~\text{Н}/\text{м}^2. $$

Оценка величины модуля упругости

Если известны значения единичной межатомной связи и, следовательно, предела прочности кристаллов, то можно оценить величину модуля упругости.

По закону Гука в пределах упругой деформации напряжение пропорционально растяжению. Коэффициент пропорциональности между величиной деформации $\eps$‍‍ и напряжением $\sigma$‍‍ (модуль упругости) $$ E=\dfrac\sigma\eps. $$

Так как величина прочности по нашей оценке $$ \sigma\approx2\cdot10^{10}~\text{Н}/\text{м}^2, $$ а максимальная упругая деформация $\eps_{\text{max}}\approx\dfrac16$‍,‍ то модуль упругости $$ E=\dfrac{2\cdot 10^{10}\cdot6}1\approx10^{11}~{\left(\dfrac{\text{Н}}{\text{м}^2}\right)}. $$

Результат расчёта по порядку величины соответствует экспериментальным данным. Например, модуль упругости стали $2\cdot10^{11}~\text{Н}/\text{м}^2$‍,‍ алюминия $0{,}7\cdot10^{11}~\text{Н}/\text{м}^2$‍,‍ каменной соли — $0{,}4\cdot10^{11}~\text{Н}/\text{м}^2$‍.‍

Оценка величины энергии связи

Зная величину единичной силы межатомной связи, можно найти величину энергии взаимодействия двух атомов. Энергия связи двух атомов определяется работой, необходимой для удаления этих атомов друг от друга на такое расстояние, при котором силы взаимодействия исчезающе малы. Это расстояние (см. рис. 1) примерно равно $2r_0$‍.‍

Для упрощения будем считать среднее значение силы взаимодействия при изменении расстояния от $r_0$‍‍ до $2r_0$‍,‍ равным $\dfrac12F_{\text{max}}$‍.‍ Тогда энергия связи (в расчёте на одну связь) равна $$ \begin{gather*} W_1=A=F\cdot l\approx F_{\text{ср}}(2r_0-r_0)\approx\dfrac{F_{max}}2\cdot r_0=\\ =\dfrac{2\cdot10^{-9}}{2}\cdot3\cdot10^{-10}=3\cdot10^{-19}~(\text{Дж}). \end{gather*} $$

Интересно сравнить полученное значение потенциальной энергии взаимодействия частиц в твёрдом теле (энергии связи) с кинетической энергией их теплового движения, определяемой в среднем величиной $kT$‍.‍ При комнатной температуре $$ W_{\text{к}}\sim kT=1{,}38\cdot10^{-23}\cdot300\approx4\cdot10^{-21}~(\text{Дж}). $$

Видно, что $W_1 \gg W_{\text{к}}$‍,‍ т. е. в твёрдом теле энергия межатомного взаимодействия много больше энергии теплового движения.

По известному значению энергии одной связи найдём энергию связи кристалла, т. е. энергию, которую необходимо затратить, чтобы разделить кристалл на отдельные атомы, и сравним полученную величину с экспериментальными значениями. На опыте величина энергии связи кристаллического вещества — это теплота испарения твёрдого тела.

Энергия связи одного моля вещества равна $$ W_{\text{св}}=W_1\,N'\,N_A, $$ где $W_1$‍‍ — энергия одной связи, $N'$‍‍ — число связей, приходящихся на один атом, $N_A$‍‍ — число Авогадро.

В рассматриваемой простейшей решётке (см. рис. 2) на каждый атом приходится по одной связи. Следовательно, величина энергии связи $$ W_{\text{св}}=3\cdot10^{-19}\cdot1\cdot6{,}02\cdot10^{23}\approx18\cdot10^{4}~{\left(\dfrac{\text{Дж}}{\text{моль}}\right)}\approx40~{\left(\dfrac{\text{ккал}}{\text{моль}}\right)}. $$

Это значение близко к найденным экспериментально значениям энергии связи различных кристаллов (несколько десятков килокалорий на моль).

Вычисление поверхностного натяжения

Пользуясь рассмотренной моделью, можно оценить и величину удельной поверхностной энергии — коэффициент поверхностного натяжения. Эта величина равна энергии, которой обладает единица поверхности на границе вещества $\Big(\alpha=\dfrac WS\Big)$‍.‍ При разрыве кристалла сечения $S$‍‍ образуется новая поверхность площадью $S_1=2S$‍‍ (рис. 4). Энергия связи единицы поверхности плоскости разрыва твёрдого тела равна $W'=W_1\,N_{\text{св}}$‍,‍ где $W_1$‍‍ — энергия одной связи, а $N_{св}$‍‍ — число связей, приходящихся на один квадратный метр. Эта энергия принадлежит как слою атомов, лежащему с одной стороны плоскости разрыва, так и слою, лежащему с другой стороны.

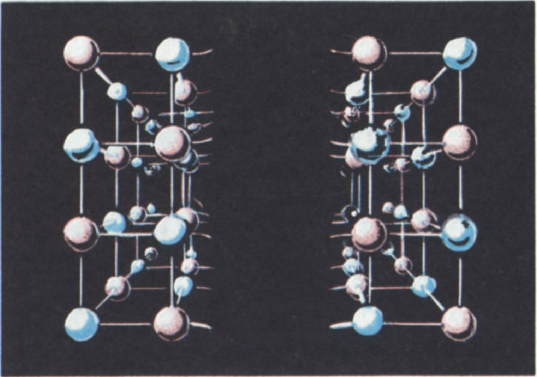
Поверхностное натяжение $$ \alpha=\dfrac W{S_1}=\dfrac{W'SN_{\text{св}}}{2S}=\dfrac{W'N_{\text{св}}}2=\dfrac{3\cdot10^{-19}\cdot10^{19}}2=1{,}5~{\left(\dfrac{\text{Дж}}{\text{м}^2}\right)}. $$ У кристалла NaCl $\alpha\approx0{,}35~\text{Дж}/\text{м}^2$‍.‍

Рассматривая взаимодействие между ионами, мы смогли оценить порядок величины предела прочности, модуля упругости, энергии связи, коэффициента поверхностного натяжения. Таким образом, мы убедились, что силы взаимодействия между ионами кристаллической решётки, т. е. силы, действующие в «микромире», определяют макроскопические свойства твёрдых тел.

Можно поступить и наоборот — по найденным экспериментально характеристикам механических свойств кристаллов определить величину сил межатомного взаимодействия. Оцените, например, величину сил межатомного взаимодействия по известному значению модуля упругости $E=10^{11}~\text{Н}/\text{м}^2$‍.‍

Оценки, которые мы проводили, делались в предположении, что рассматриваемый кристалл имеет идеальную структуру решётки. У реальных кристаллов правильность решётки нарушается. Учёт этого факта значительно усложняет теоретические расчёты характеристик физических свойств кристаллов. Некоторые из сделанных нами оценок для идеальных кристаллов значительно расходятся с данными, получаемыми из экспериментов.