Изображения страниц
Текст статьи [Задачи] // Квант. — 1973. — № 1. — С. Обложка (с. 3).
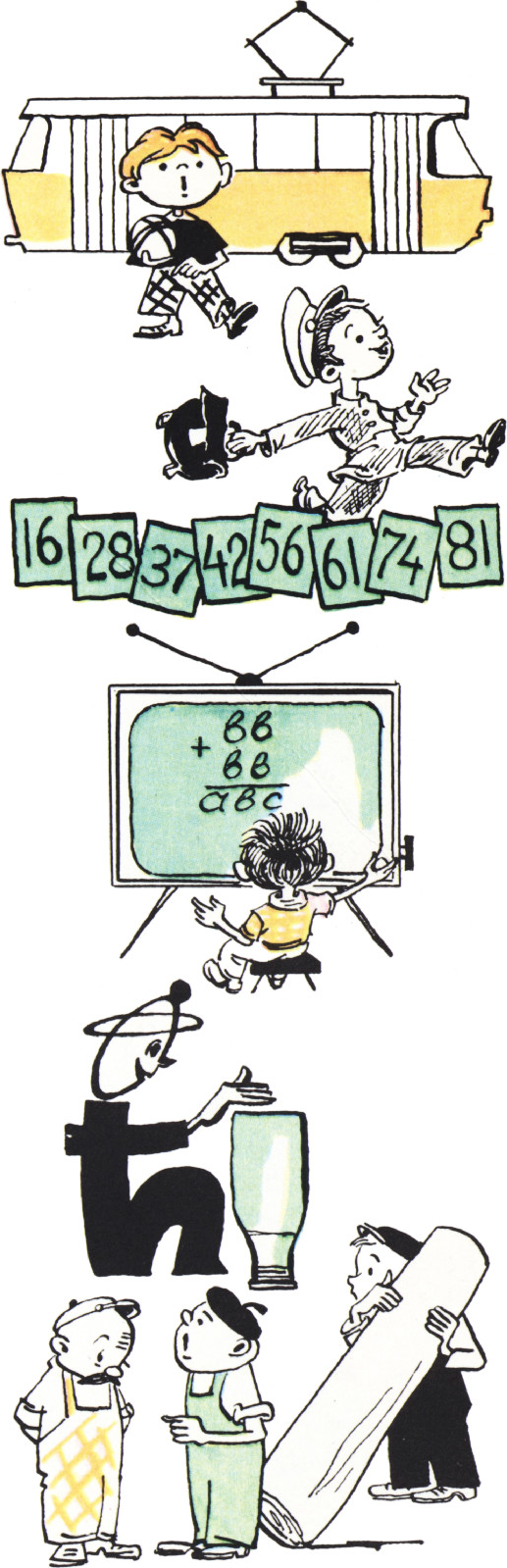
Двое приятелей не виделись много лет. Встретившись, они разговорились, и один похвалился другому, что у него уже трое детей. «Сколько же им лет?», — спросил второй. «Произведение их лет равно 36, а сумма — номеру вот этого проезжающего трамвая». Посмотрев на номер трамвая, второй собеседник сказал, что этих данных недостаточно. «А старший сын у меня рыжий», — «Тогда я знаю, сколько им лет», — сказал его приятель и точно назвал возраст каждого ребёнка.
Сколько же лет было каждому ребёнку?
На очередном занятии математического кружка каждый школьник получил 8 карточек с числами. Требовалось разложить карточки в две строчки (по 4 карточки в строчку) так, чтобы суммы чисел строчек были равны между собой.
Один из играющих разложил карточки в одну строчку так, как показано на рисунке, и немедленно заявил комиссии, что задача не имеет решения. Почему ученик, не занимаясь подробным подсчётом, сделал такое заявление? И как всё-таки решить зaдачу?
- Расшифруйте пример на сложение: $$ \def\-#1{\enspace\mathclap{#1}\enspace} \colsep{0pt}{\begin{array}{ccc} &\-b&\-b\\[-6pt] \-+\\[-6pt] &\-b&\-b\\ \hline \-a&\-b&\-c \end{array}} $$
- Переверните нераспечатанную бутылку кефира и постучите по донышку так, чтобы брызнул кефир (для осторожности, проделайте всё это над глубокой тарелкой). Что сделается с крышкой и почему?
- Два человека несут бревно, поддерживая его на одинаковых расстояниях от концов. Третий, желая помочь, берётся за бревно впереди первого. Будет ли легче несущим бревно? (Или: что скажет второй?)
Ответы, указания, решения
- Есть лишь один случай, когда, зная номер трамвая, нельзя определить возраст детей; отсюда находим номер трамвая. Указание, что один из детей — старший, исключает случай со старшими близнецами.
- Сумма чисел всех карточек нечётна. Однако можно перевернуть карточки с числом 16 (получив 91) и некоторые другие.
$a=1$, $b=9$, $c=8$. - Под действием атмосферного давления крышечка «втянется» в бутылку (давление на неё сверху уменьшится).
- Второму человеку, несущему бревно, станет от этой «помощи» тяжелее. Убедиться в этом вы можете на собственном опыте илн воспользовавшись правилом рычага.
