Изображения страниц
Текст статьи Берколайко С. Т. Задачи на неравенства // Квант. — 1972. — № 8. — С. 16, 25.
- Доказать неравенство $$ \begin{gathered} \sqrt{x_1^2+(1-x_2)^2}+ \sqrt{x_2^2+(1-x_3)^2}+{}\\{}+ \sqrt{x_3^2+(1-x_4)^2}+\ldots+ \sqrt{x_{2n}^2+(1-x_1)^2}\ge\sqrt2\cdot n. \end{gathered} $$
- Определить, что больше:
$\sqrt[3]{10}+\sqrt8$ или 5? - Доказать, что $$
\dfrac{2-\sqrt{2+\sqrt{2+\sqrt{2+\ldots+\sqrt2}}}}
{2-\sqrt{2+\sqrt{2+\ldots+\sqrt2}}}\gt\dfrac14
$$
(в числителе
$n$ радикалов; в знаменателе$n-1$ радикалов). - Доказать неравенство $$ \sqrt{5x+15}+\sqrt{8-8x}\le7. $$
- Определить, что больше:
$\sqrt[3]2+\sqrt[3]{18}$ или 4? - Доказать, что выражение $$ \sqrt{2-\sqrt{2-\ldots-\sqrt{2-\sqrt2}}} $$ меньше 1 для чётного числа радикалов и больше 1 для нечётного числа радикалов.
Ответы, указания, решения
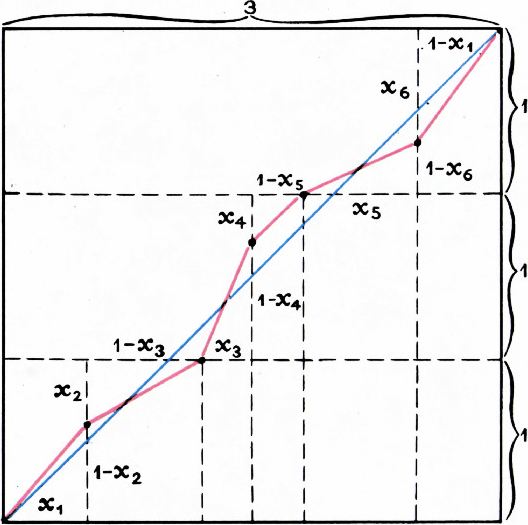
Задача допускает интересное геометрическое решение, основанное на теореме Пифагора. На рисунке дано решение для
$n=3$. Длина ломаной, нарисованной красным цветом, — левая часть неравенства, длина диагонали — правая часть. Знак равенства имеет место лишь при выполнении следующих условий: $$ \begin{gathered} x_1=x_3=\ldots=x_{2n-1};\quad x_2=x_4=\ldots=x_{2n}\\ \text{и}\quad x_1+x_2=1. \end{gathered} $$ В этом случае ломаная сливается с диагональю квадрата.
- Достаточно установить знак неравенства $$ \sqrt[3]{10}-2\vee3-\sqrt8. $$ Для этого воспользоваться тождеством $$ (\sqrt[3]{10}-2)(\sqrt[3]{100}+2\sqrt[3]{10}+4)=(3-\sqrt8)(6+2\sqrt8)=2. $$
Прежде всего покажем, что $$ x=\underbrace{\sqrt{2+\sqrt{2+\ldots+\sqrt2}}}_{n-1~\text{радикалов}}\lt2. $$ Действительно, заменив последний из радикалов
$\sqrt2$ на 2, мы увеличим$x$, т. е. $$ x\lt\sqrt{2+\sqrt{2+\ldots+\sqrt{2+2}}}=\ldots=\sqrt{2+2}=2. $$Перепишем исходное неравенство так:
$4(2-\sqrt{2+x})\gt2-x$ и далее $$ (2-\sqrt{2+x})^2\gt0. $$- Указание. Оценить сумму $$ \underbrace{\dfrac15\sqrt{5x+15}+\ldots+\dfrac15\sqrt{5x+15}}_ {5~\text{слагаемых}}+\dfrac12\sqrt{8-2x}+\dfrac12\sqrt{8-2x}. $$
Указание. Определить, что больше:
$3-\sqrt[3]{18}$ или$\sqrt[3]2-1$. Ответ:
$\sqrt[3]2+\sqrt[3]{18}\lt4$. - Указание. Воспользоваться неравенством
$\sqrt2\gt1$.

