Изображения страниц
Текст статьи [Задачи] // Квант. — 1972. — № 6. — С. Обложка (с. 3).

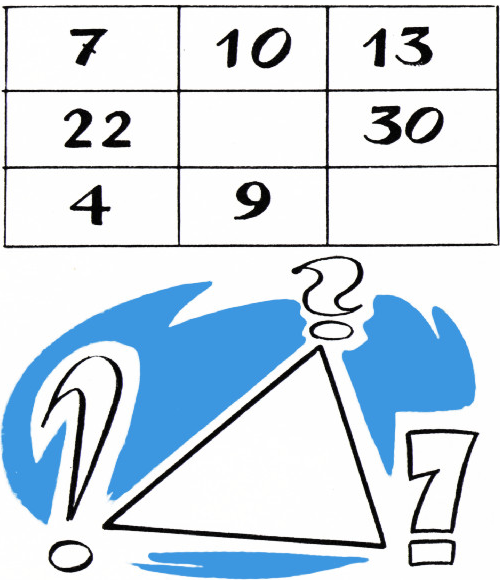
- Вписать в пустые клетки на рисунке недостающие числа.
- Около каждой вершины треугольника поставьте какое-нибудь число. Напишите возле каждой стороны этого треугольника число, равное сумме чисел, стоящих у её концов. Теперь каждое число, стоящее около вершины, сложите с числом, стоящим около противоположной стороны. Почему равны все три получившиеся суммы?
- Найдите нечётное четырёхзначное число, две средние цифры которого образуют число, в пять раз большее числа тысяч и в три раза большее числа единиц этого числа.
- Может ли выражение
$\dfrac{a+9}{a+6}$ ($a$ — целое) быть целым числом? Если да, то при каких значениях$a$? В двух комнатах было 76 человек. Когда из одной комнаты вышло 30, а из второй 40 человек, то людей в комнатах осталось поровну. Сколько человек было в каждой комнате первоначально?
Представьте себе, что вы машинист. Машинист ведёт поезд из Москвы во Владивосток. В составе 64 вагона, 14 вагонов с мебелью, 30 вагонов с бурым углём, 20 вагонов с солью. Делаете 3 остановки по 15 минут. До первой остановки поезд шёл со скоростью 60 км/ч. Сколько лет машинисту?

Ответы, указания, решения
- 26, 14.
- Каждая сумма равна сумме чисел, стоящих у вершин треугольника.
- 3155.
$-3$, $-5$, $-7$, $-9$. - 33, 43.
- А сколько вам лет?
