Изображения страниц
Текст статьи [Задачи] // Квант. — 1972. — № 5. — С. Обложка (с. 3).


- К стене прислонён обруч. В одной точке в стене «внутри» обруча вбит гвоздь так, что обруч касается его. Найти геометрическое место точек, в которые надо вбить второй гвоздь внутри обруча, чтобы обруч оставался неподвижным.
В предлагаемой шифровке значками зашифрованы цифры и знаки
$+$, $-$, $=$. Каждая строчка шифровки содержит запись одного из арифметических действий типа: $$ 25+184=209\quad\text{или}\quad2568=2573-5. $$Попробуйте определить, какой цифре или знаку соответствует каждый из значков.
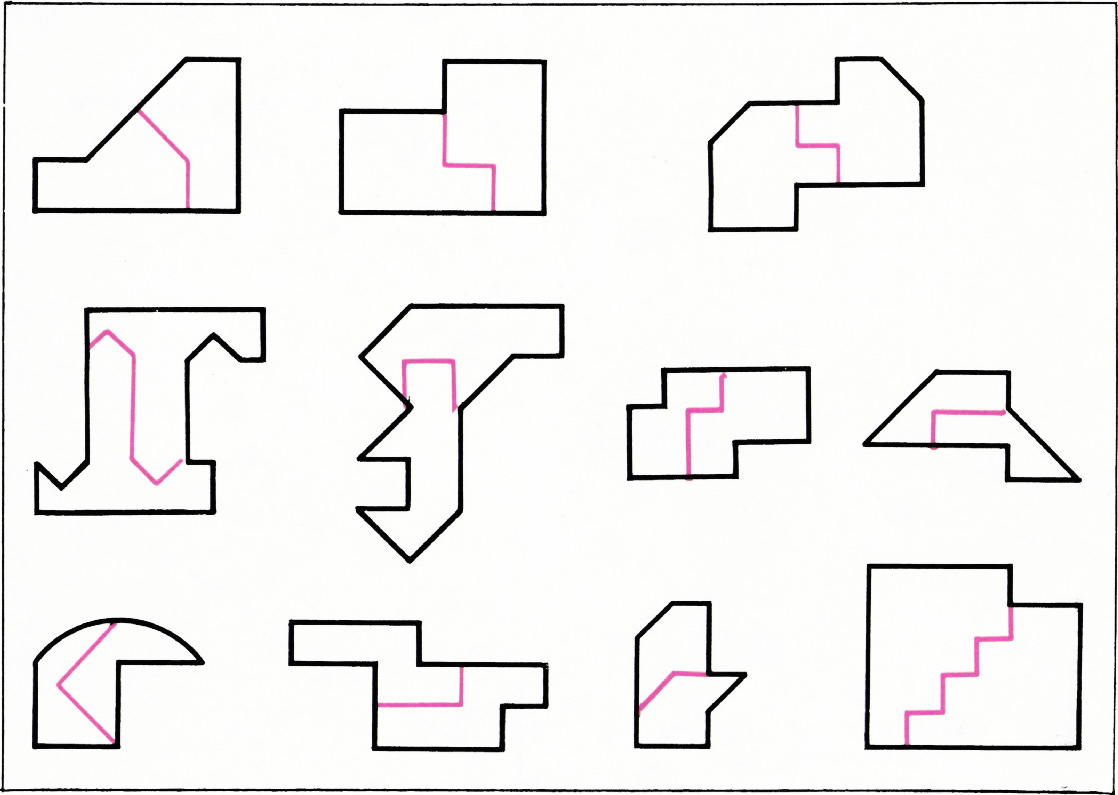
Каждую из приведённых фигур, попробуйте разрезать на две равные фигуры, т. е. на две такие фигуры, которые можно совместить, наложив одну на другую.
В качестве примера на первой из этих фигур показан требуемый разрез.
Ответы, указания, решения
- Искомым геометрическим местом точек является дуга «внутренней окружности» обруча от «северного полюса» до точки, диаметрально противоположной той точке на стенке, куда вбит гвоздь.
Сначала определим, какой из значков соответствует знаку
$=$. Этот знак встречается по одному разу в каждой строчке, при этом он не может стоять ни в начале, ни в конце строки. Отсюда легко определить, что это$\sqcap$. Сравнивая число значков слева и справа от него, легко определить, что знаку$+$ соответствует значок$\mkern2mu\htmlStyle {display:inline-block;transform:rotate(90deg);}{{\ominus}\mkern-2mu}$, а знаку$-$ соответствует значок$\lt$. Подставив найденные значки, получим: $$ \def\r#1{\textcolor{red}{\bm{#1}}} \def\sq{\mathrlap{\sqcap}{\sqcup}} \colsep{1pt}{\begin{array}{ccccccccccc} \gt&\sqsupset&\ominus&\r=&\vee&\oplus&\ominus&\r-&\sq&\sq&\sqcup\\ \vee&\wedge&\ominus&\r+&\gt&\vee&\r=&\sq&\sqcup&\sq&\wedge\\ \oplus&\wedge&\sqcup&\ominus&\r=&\oplus&\sq&\vee&\vee&\r+&\sqsubset\\ \sq&\sqcup&\sqsubset&\sqsubset&\r-&\gt&\vee&\r=&\vee&\ominus&\small\bigcirc \end{array}} $$ Очевидно, что
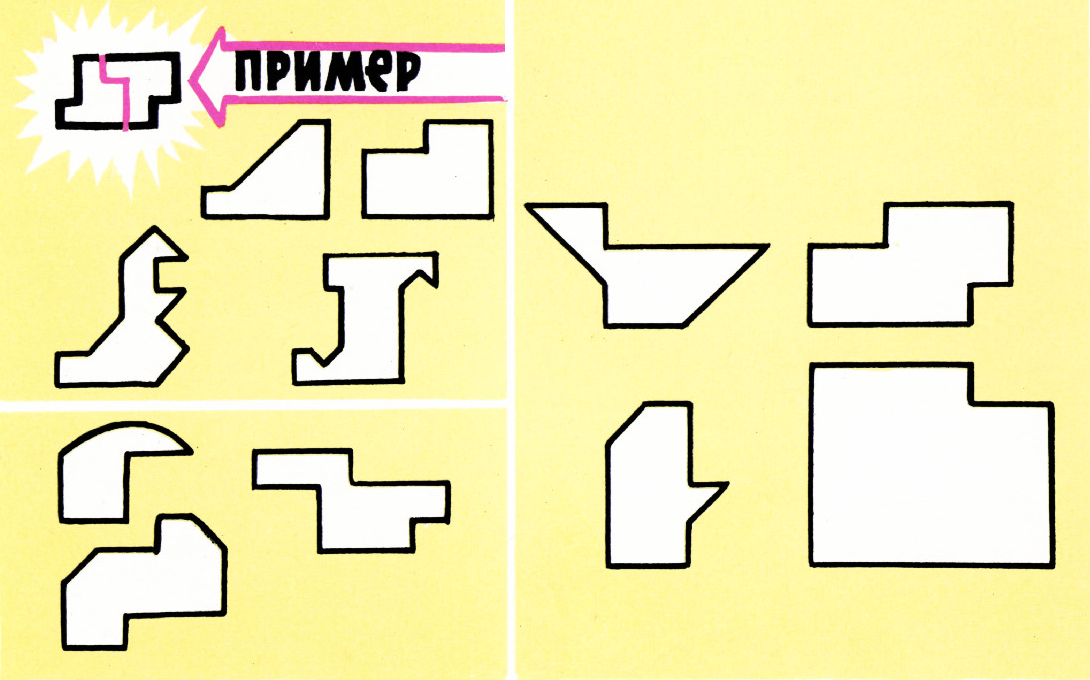
$\mathrlap{\sqcap}{\sqcup}$ это 1, а$\vee$ — 9, далее легко находятся цифры, соответствующие остальным значкам:$\wedge$ — 2,$\ominus$ — 3,$\sqsubset$ — 4,$\small\bigcirc$ — 5,$\sqsupset$ — 6,$\oplus$ — 7,$\gt$ — 8.- См. рисунок.