Бендукидзе А. Д.

Архимед и квадратура параболыБендукидзе А. Д. Архимед и квадратура параболы // Квант. — 1971. — № 7. — С. 7‍—‍10.‍‍

Кому не известно имя Архимеда? Этот великий мыслитель оставил неизгладимый след в истории человечества. Исследователи его творчества с восхищением говорят о нём как о великом инженере, об астрономе-наблюдателе, не имеющем себе равных, о гениальном математике, о человеке, знающем все тайны природы...

Математические работы Архимеда подкупают читателя ясностью мысли, изяществом, доведённой до совершенства техникой вычислений. Известный греческий историк Плутарх пишет:

«Во всей геометрии нельзя найти более трудных и глубокомысленных задач, которые были бы решены так просто и ясно, как те, которыми занимался Архимед».

Не является исключением и одна из первых математических работ Архимеда — «Квадратура параболы».

Эта работа посвящена вычислению площади параболического сегмента, т. е. фигуры, ограниченной параболой и прямой, и представляет, в сущности, доказательство следующей теоремы:

Площадь параболического сегмента равна четырём третьим площади треугольника, имеющего с сегментом общее основание и высоту.

Работа естественным образом делится на две части. В первой части Архимед показывает, как эта теорема была им обнаружена при помощи механики, а именно при помощи им же установленного «закона рычага», во второй же части даёт её геометрическое доказательство.

Мы познакомим читателя с содержанием второй части работы.

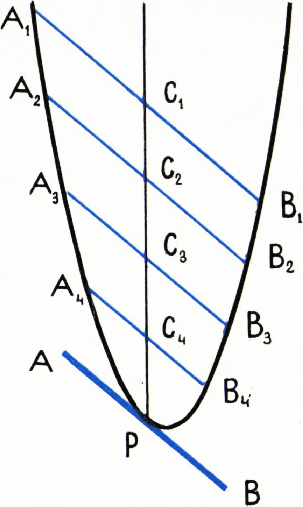
1. Сформулируем одно замечательное свойство параболы‍, на котором основано всё дальнейшее изложение.

Если прямая $AB$‍‍ касается параболы в точке $P$‍‍ и хорды $A_1B_1$‍,‍ $A_2B_2$‍,‍ $A_3B_3$‍,‍ $\ldots$‍‍ параллельны этой касательной, то середины хорд — точки $C_1$‍,‍ $C_2$‍,‍ $C_3$‍,‍ $\ldots$‍‍ — лежат на одной прямой; эта прямая параллельна оси параболы и проходит через точку $P$‍‍ (рис. 1).

Кроме того, $$ \dfrac{A_1C_1^2}{PC_1}=\dfrac{A_2C_2^2}{PC_2}=\dfrac{A_3C_3^2}{PC_3}=\ldots \tag1 $$

Попробуйте доказать эти свойства параболы сами.

2. Рассмотрим теперь параболический сегмент, ограниченный дугой параболы $APB$‍‍ и хордой $AB$‍‍ (рис. 2).

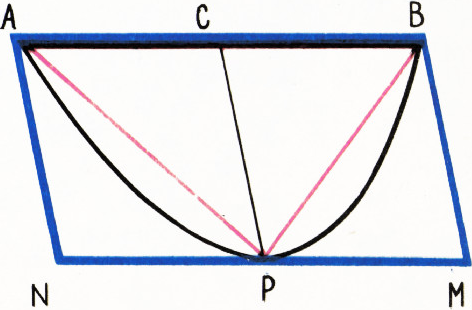
Точку параболы $P$‍,‍ касательная в которой параллельна хорде $AB$‍,‍ назовём вершиной сегмента, а саму хорду $AB$‍‍ — основанием сегмента. $C$‍‍ — середина основания. Согласно свойству (1) прямая $PC$‍‍ параллельна оси параболы.

Впишем в сегмент треугольник $APB$‍‍ и опишем около сегмента параллелограмм $ABMN$‍‍ ($AN\parallel BM\parallel PC$‍).‍

Так как площадь треугольника $APB$‍‍ равна половине площади параллелограмма $ABMN$‍,‍ она больше половины площади сегмента, и поэтому сумма площадей двух оставшихся по краям сегментов меньше половины площади всего сегмента. Если в эти оставшиеся сегменты тем же способом вписать треугольники, то сумма их площадей будет больше половины суммы площадей самих сегментов, и поэтому сумма площадей оставшихся после второго вписывания четырёх сегментов будет меньше одной четверти площади данного сегмента. Если далее в эти четыре сегмента тем же способом вписать треугольники, то вне этих треугольников останутся восемь маленьких сегментов, сумма площадей которых будет меньше одной восьмой площади данного сегмента, и т. д.

Таким образом, продолжая этот процесс, в сегмент можно будет вписать такой многоугольник, что сумма площадей сегментов, оставшихся вне этого многоугольника, будет сколь угодно малой.

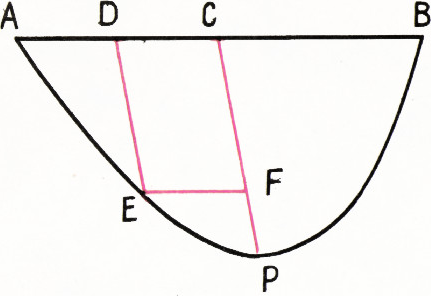
3. Разделим отрезок $AC$‍‍ пополам и через точку деления $D$‍‍ проведём прямую $DE$‍,‍ параллельную $PC$‍‍ (рис. 3). Докажем, что $$ PC=\dfrac43ED.\tag2 $$ В самом деле, если провести $EF\parallel AC$‍,‍ то согласно равенствам (1) можем написать что $\dfrac{AC^2}{PC}=\dfrac{EF^2}{PF}$‍.‍

Поскольку $AC=2EF$‍,‍ $PC=4PF$‍.‍

Таким образом, $FC=ED=3PF$‍;‍ отсюда уже получается требуемое равенство.

4. После того как в сегмент был вписан треугольник $APB$‍,‍ по краям осталось два сегмента. Впишем в эти сегменты тем же способом треугольники $AEP$‍‍ и $PKB$‍‍ (рис. 4).

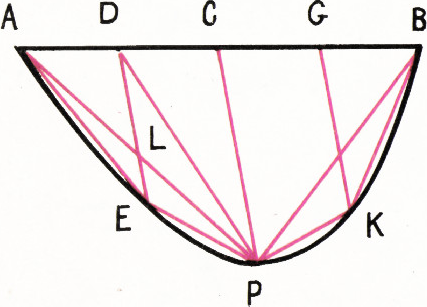
Докажем, что площадь треугольника $APB$‍‍ в восемь раз больше площади каждого из этих треугольников. Для доказательства заметим, что если через вершину $E$‍‍ сегмента $AEP$‍‍ провести прямую $ED$‍,‍ параллельную оси параболы, она по свойству 1 разделит хорду $AP$‍,‍ а следовательно, и отрезок $AC$‍‍ пополам. Таким образом, $AD=DC$‍.‍ Далее, так как $PC=2LD$‍,‍ из равенства (2) следует, что $3LD=2ED$‍.‍ Отсюда в свою очередь получаем, что $$ LD=2EL.\tag3 $$

Рассмотрим теперь треугольники $ADL$‍‍ и $ALE$‍.‍ Их основания $DL$‍‍ и $EL$‍‍ лежат на одной прямой, а вершина $A$‍‍ — общая. Поэтому с учётом равенства (3) имеем $S_{\triangle ADL}=2S_{\triangle ALE}$‍.‍

Подобным же образом, так как основания $DL$‍‍ и $LE$‍‍ треугольников $DLP$‍‍ и $LEP$‍‍ лежат на одной прямой, а $P$‍‍ — их общая вершина, имеем $S_{\triangle DLP}=2S_{\triangle LEP}$‍.‍

Из последних двух равенств $S_{\triangle APD}=2S_{\triangle AEP}$‍‍ и учитывая, что $S_{\triangle APB}=4S_{\triangle APD}$‍,‍ получим окончательно $S_{\triangle APB}=8S_{\triangle AEP}$‍.‍

Аналогично доказывается и второе равенство: $S_{\triangle APB}=8S_{\triangle PKB}$‍.‍

Если площадь треугольника $APB$‍‍ обозначить через $s_1$‍,‍ а сумму площадей треугольников $AEP$‍‍ и $PKB$‍‍ — через $s_2$‍,‍ то согласно доказанному $s_1=4s_2$‍.‍ На рисунке 5 эти площади окрашены соответственно оранжевым и синим.

5. Продолжим процесс вписывания треугольников. Площадь первого треугольника обозначим через $s_1$‍,‍ сумму площадей треугольников, вписанных на втором шаге, — через $s_2$‍,‍ сумму площадей четырёх треугольников, вписанных на третьем шаге, — через $s_3$‍‍ и т. д.

Получим бесконечную числовую последовательность $$ s_1,~s_2,~s_3,~\ldots,~s_n,~\ldots,\tag4 $$ в которой каждый член, начиная со второго, в четыре раза меньше предыдущего‍, т. е. $$ s_2=\dfrac14s_1,~s_3=\dfrac14s_2,~\ldots,s_{n+1}=\dfrac14s_n,~\ldots\tag5 $$

Докажем одно замечательное свойство этой последовательности, а именно докажем, что для любого $n$‍‍ справедливо следующее равенство: $$ s_1+s_2+\ldots+s_{n-1}+s_n+\dfrac43s_n=\dfrac43s_1.\tag6 $$

В самом деле, так как $$ 4(s_1+s_2+\ldots+s_{n-1}+s_n)=4s_1+(4s_2+4s_3+\ldots+4s_{n-1}+4s_n), $$ из соотношений (5) следует, что $$ 4(s_1+s_2+\ldots+s_{n-1})+4s_n=4s_1+(s_1+s_2+\ldots+s_{n-1}), $$ то есть $$ 3(s_1+s_2+\ldots+s_{n-1})+4s_n=4s_1. $$

Равенство (6) получается отсюда делением на 3.

6. Теперь уже можно доказать, что площадь параболического сегмента $S=\dfrac43s_1$‍.‍

Архимед доказывает это равенство так называемым «методом исчерпывания». Этот метод, принадлежащий одному из крупнейших греческих математиков — Евдоксу (IV век до н. э.), заменял во времена Архимеда метод предельного перехода.

Предположим, что $S\gt\dfrac43s_1$‍‍ или $S\lt\dfrac43s_1$‍.‍

Докажем, что это невозможно.

Предположим сначала, что $$ S\gt\dfrac43s_1.\tag7 $$

Мы уже отмечали, что, продолжая процесс вписывания, можно добиться того, чтобы сумма площадей оставшихся сегментов была сколь угодно малой. Это значит, что, подбирая соответствующим образом $n$‍,‍ разность $S-(s_1+s_2+\ldots+s_n)$‍‍ можно сделать меньше любого наперёд заданного положительного числа. Подберём $n$‍‍ так, чтобы выполнялось неравенство $$ S-(s_1+s_2+\ldots+s_n)\lt S-\dfrac43s_1. $$ Тогда $$ s_1+s_2+\ldots+s_n\gt\dfrac43s_1, $$ а это, согласно равенству (6), невозможно‍. Таким образом, неравенство (7) неверно.

Предположим теперь, что $$ S\lt\dfrac43s_1.\tag8 $$

Так как члены последовательности (4) стремятся к нулю, $n$‍‍ можно выбрать так, чтобы выполнялось следующее неравенство: $$ \dfrac43s_n\lt\dfrac43s_1-S. $$

Из этого неравенства с учётом равенства (6) получим $$ S\lt s_1+s_2+\ldots+s_{n-1}+s_n. $$ что, конечно же, невозможно.

Итак, и неравенство (8) неверно. Тем самым доказано, что $S=\dfrac43s_1$‍.‍

7. Сделаем в заключение следующее замечание.

Как известно, древние греки под квадратурой фигуры понимали построение квадрата, равновеликого этой фигуре. Задача о квадратуре в «греческом смысле» не всегда имеет решение. Доказано, например, что для круга она неразрешима. Т. е. нельзя построить (при помощи циркуля и линейки) квадрат, равновеликий данному кругу.

Полученный Архимедом результат примечателен и в том смысле, что показывает возможность положительного решения задачи о квадратуре параболического сегмента: зная основание и высоту сегмента, всегда можно построить квадрат, равновеликий этому сегменту.