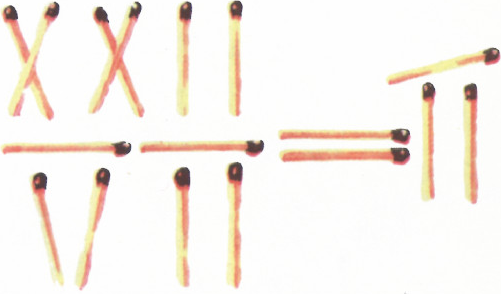Изображения страниц
Текст статьи [Задачи] // Квант. — 1971. — № 4. — С. Обложка (с. 3).



- За какое наименьшее число разломов можно полностью разломить шоколадку (рис. 1) на кусочки? Ломать можно только по прямым, являющимся углублениями на шоколадке.
- Здесь зашифровано хорошо известное стихотворение. Можете ли вы его расшифровать? $$ \begin{array}{l} \text{Мяжя Дяма клёнгё брящэд,}\\ \text{Юлёмыря ф лэщгю нащыг.}\\ \text{Дыжэ, Дямэщгя, мэ брящъ,}\\ \text{Мэ юдёмэд ф лэщгэ нащ.} \end{array} $$
- На рисунке 2 изображены три верёвочных кольца. Если разрезать верхнее кольцо, то остальные окажутся свободными, если же разрезать одно из нижних, то оставшиеся будут сцепленными. Попробуйте сцепить три кольца так, чтобы при разрезании любого из них оставшиеся кольца оказались свободными.
- Здесь крестиками зашифрованы некоторые цифры. Попробуйте расшифровать пример. $$ \def\X{\enspace\mathclap{\times}\enspace}\let\x\times \def\-{\mathclap{\rule[-3.7pt]{1.1em}{-3.3pt}}} \def\|{\rule[-3.5pt]{.4pt}{12pt}} \def\m{\quad\mathllap{-}} \colsep{0pt}{\begin{array}{rccccccccccccccccc} &\X&\X&7&\X&\X&\X&\X&\X&\X&\X&\|&\X&\X&\X&\X&7&\X\\[-12pt] &&&&&&&&&&&\|&\-&\-&\-&\-&\-&\-\\[-6pt] -\\[-6pt] &\x&\x&\X&\x&\x&\x&&&&&\|&\x&\x&7&\x&\X\\[-12pt] &\-&\-&\-&\-&\-&\-&\-\\ &\x&\x&\x&\x&\x&7&\x\\[-6pt] -\\[-6pt] &\x&\x&\x&\x&\x&\x&\x\\[-12pt] &\-&\-&\-&\-&\-&\-&\-&\-\\ &&&\x&7&\x&\x&\x&\x\\[-6pt] &&\m\\[-6pt] &&&\x&7&\x&\x&\x&\x\\[-12pt] &&&\-&\-&\-&\-&\-&\-&\-\\ &&&\x&\x&\x&\x&\x&\x&\x\\[-6pt] &&\m\\[-6pt] &&&\x&\x&\x&\x&7&\x&\x\\[-12pt] &&&\-&\-&\-&\-&\-&\-&\-&\-\\ &&&&&\x&\x&\x&\x&\x&\x\\[-6pt] &&&&\m\\[-6pt] &&&&&\x&\x&\x&\x&\x&\x\\[-12pt] &&&&&\-&\-&\-&\-&\-&\-\\ &&&&&&&&&&0 \end{array}} $$
Равенство, изображённое на рисунке 3, неверно. Переложите одну спичку так, чтобы оно выполнялось с точностью до 0,01.
Подсказка. Посмотрите статью Н. М. Бескина «Цепные дроби» («Квант» № 1, 1970).
Ответы, указания, решения
- Заметим, что при каждом разломе мы увеличиваем число кусков на один.
Общее число кусков равно
$4\cdot8=32$. До разламывания мы имели один кусок, после первого разламывания их оказалось два, после второго разламывания три,$\ldots$, после 31-го разламывания 32. Таким образом, в каком бы порядке мы ни ломали шоколадку, нам всегда придётся ломать её ровно 31 раз. Шифр заключается в следующем: твёрдые гласные заменены на соответствующие им мягкие, а мягкие на твёрдые (а на я, у на ю и т. д.); аналогично, звонкие согласные заменены на глухие, а глухие на соответствующие им звонкие (б на п, в на ф, г на к и т. д.); кроме того, произведена перестановка шипящих и свистящих согласных (щ—ч, х—ц) и знаков ъ—ь.
Ответ:$$ \begin{array}{l} \text{Наша Таня громко плачет,}\\ \text{Уронила в речку мячик.}\\ \text{Тише, Танечка, не плачь,}\\ \text{Не утонет в речке мяч.} \end{array} $$
- Требуемый способ изображён на рисунке 1.
$7\,375\,428\,413:125\,473=58\,781$. - Новое расположение спичек изображено на рисунке 2.