Изображения страниц
Текст статьи Готман Э. Г. Вспомогательная окружность // Квант. — 1971. — № 1. — С. 28—31.
Решение многих геометрических задач начинается с проведения вспомогательных линий, которые помогают установить связь между данными и неизвестными элементами фигуры. Отыскать удачное вспомогательное построение часто бывает нелегко. Поэтому к каждой решённой задаче следует присмотреться и постараться выяснить, почему те или иные вспомогательные линии приводят к цели. Нельзя ли найденный приём использовать при решении некоторых других задач?
На очередном заседании математического кружка рассмотрим один из интересных приёмов решения геометрических задач, который состоит в том, что в чертеже вводится вспомогательная окружность.
Пример 1. В остроугольном треугольнике проведены высоты
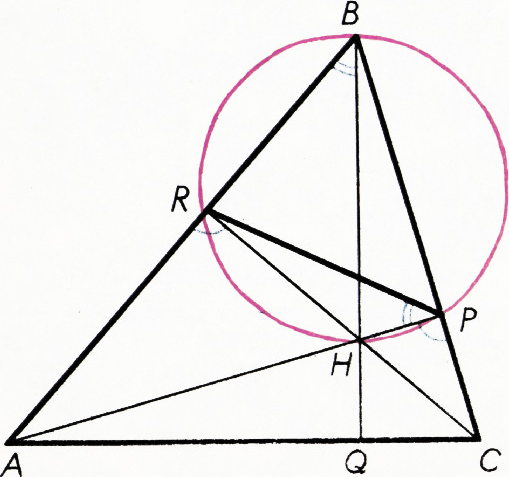
Решение. Пусть
Таким образом, построение вспомогательной окружности позволило использовать теорему о вписанных углах и благодаря этому установить связь между указанными в задаче углами.
Выясните, как изменится результат, если
Решите самостоятельно несколько аналогичных задач.
1. Из произвольной точки
2. Доказать, что прямая, соединяющая вершину прямого угла прямоугольного треугольника с центром квадрата, внешне построенного на гипотенузе, делит прямой угол треугольника пополам.
3. Из произвольной точки
Пример 2. Доказать, что отрезок, соединяющий основания двух высот остроугольного треугольника, отсекает от него треугольник, подобный данному.
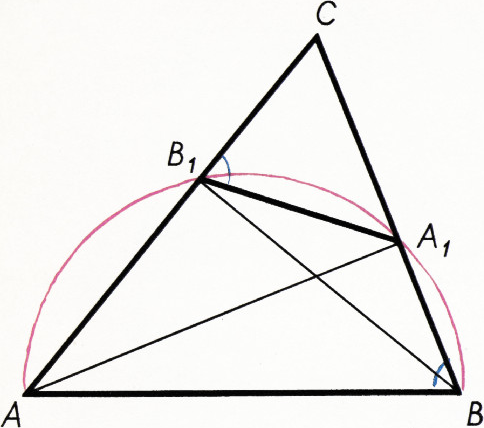
Решение. Пусть
Эту задачу можно решить и без вспомогательных построений, если заметить,
что треугольники
Решите каждую из двух следующих задач обоими способами.
4. Из вершины
5. Из основания
Иногда выгодно описать окружность и около треугольника.
Пример 3. Доказать, что квадрат биссектрисы треугольника равен разности между произведением заключающих её сторон и произведением отрезков третьей стороны, на которые она делится биссектрисой.
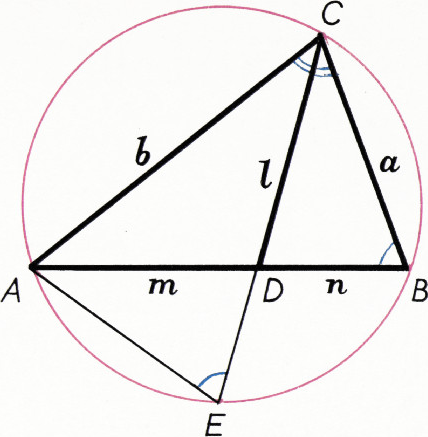
Решение. Около треугольника
По условию
Пример 4. Высота и медиана треугольника, проведённые из одной вершины внутри него, различны и образуют равные углы со сторонами, выходящими из той же вершины. Доказать, что треугольник прямоугольный.
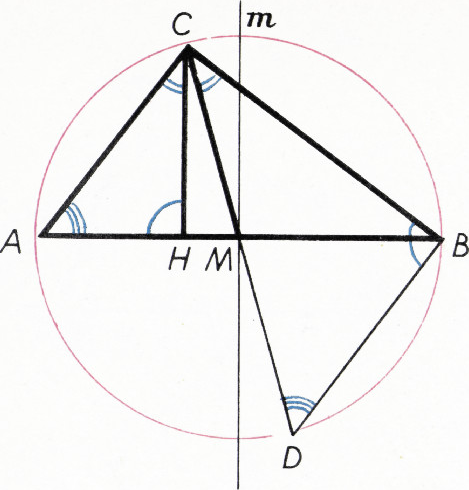
Решение. Пусть высота
Центр окружности лежит на диаметре
Используйте полученный результат для решения следующих двух задач.
6. Определить углы треугольника, в котором
- медиана и высота, проведённые из одной вершины, делят угол на три равные части;
- медиана, биссектриса и высота, проведённые из одной вершины, делят угол при этой вершине на четыре равные части.
7. Построить треугольник, зная углы, которые образуют медиана, биссектриса и высота, выходящие из одной вершины.
Пример 5. Построить равносторонний треугольник так, чтобы вершины его лежали соответственно на трёх данных параллельных прямых.
Известно несколько решений этой интересной задачи с использованием вращения вокруг точки, подобия и алгебраического метода. Весьма краткое решение получается с помощью построения вспомогательной окружности.
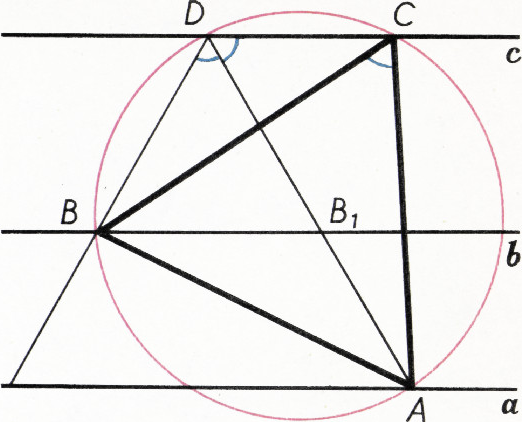
Решение. Пусть
Отсюда вытекает следующее построение. Из произвольной точки
Отложим на прямой
Таким образом, приём построения вспомогательной окружности целесообразно применять и при решении некоторых задач на построение.
Рассмотрим ещё одну более сложную задачу, при решении которой самое трудное — догадаться описать около квадратов окружности.
Пример 6. На сторонах
Решение. Если
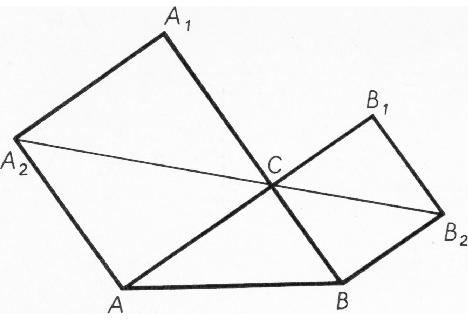
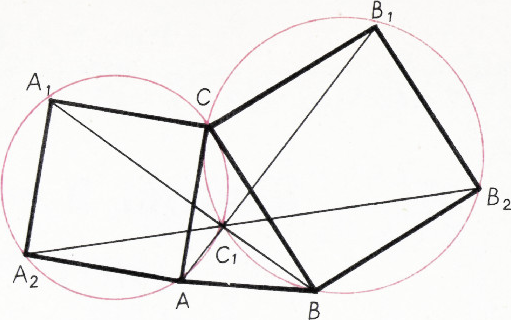
Если
Точно так же доказывается, что точка
Рассматривая полученные вписанные углы, находим, что прямые
Следующая задача имеет много общего с предыдущей.
8. На сторонах
9. Доказать, что если два противоположных угла четырёхугольника тупые, то диагональ, соединяющая вершины этих углов, короче второй диагонали.
Приведём ещё две задачи на максимум и минимум, для решения которых также целесообразно определённым образом построить вспомогательную окружность.
10. На одной стороне угла с вершиной в точке
11. Из произвольной точки
Таким образом, разнообразные геометрические задачи решаются с помощью одного и того же приёма. Построение вспомогательной окружности позволяет увеличить число теорем, которыми можно пользоваться при решении задачи, и благодаря этому отыскивать зависимость между элементами фигуры.
Ответы, указания, решения
- Переобозначьте точки:
$A$ через$B$, $C$ через$P$, $M$ через$H$ и$N$ через$R$ — и посмотрите на рисунок 1 в тексте. - Соедините остальные вершины треугольника с центром квадрата. Получившиеся отрезки равны, на них опираются нужные углы.
- Проведите окружность через точки
$A$, $P$, $M$, $Q$ и перепишите для дуг условие$\angle APN=\angle AQM$ (то, что они равны$90^\circ$, даже не используется, лишь бы точки$A$, $P$, $M$, $Q$ лежали на одной окружности). - Проведите окружность через точки
$A$, $M$, $C$. Треугольники подобны по двум углам, опирающимся на дуги$AM$ и$AN$. - Проведите окружность через точки
$C$, $M$, $N$, $H$. Воспользуйтесь тем, что$CH$ — диаметр, и докажите, что$\angle BAC=\angle CNM$. $90^\circ$; $60^\circ$; $30^\circ$. $90^\circ$; $22{,}5^\circ$; $67{,}5^\circ$.
- Треугольник определяется с точностью до подобия. Возьмите произвольную точку на биссектрисе, считайте её точкой пересечения биссектрисы с описанной окружностью. Перпендикуляр, опущенный из этой точки на сторону треугольника (он параллелен высоте), попадает в основание медианы и проходит через центр окружности. Третья точка на окружности получится отражением в этом перпендикуляре. Не забудьте провести анализ возможности построения и рассмотреть все возможные случаи.
- Ключ к решению этой задачи дают вспомогательные окружности, описанные
около равносторонних треугольников и пересекающиеся в одной точке, через
которую прсходят и все три прямые
$AA_1$, $BB_1$, и$CC_1$. Пусть на стороне
$AB$ треугольника$ABC$ как на диаметре построена окружность. Докажите, что если угол$C$ тупой, то его вершина лежит внутри окружности.А теперь подумайте, как следует построить окружность, чтобы решить задачу 9.
- Окружность, проведённая через
$A$, $B$, $C$, должна касаться стороны угла в точке$C$. Докажите, что$\angle SCA=\angle SBC$. Треугольники$SAC$ и$SBC$ подобны. Для определения$SC$ можно провести любую окружность через точки$A$ и$B$ и определить длину отрезка касательной, проведённой из точки$S$, от$S$ до точки касания. Это и будет$SC$. - При решении этой задачи можно применить формулу, выражающую сторону треугольника через диаметр описанной окружности и противолежащий угол.



