Изображения страниц
Текст статьи Андреев Е. М. Невписываемые многогранники // Квант. — 1970. — № 8. — С. 2—9.

Рассмотрим куб, одна из вершин которого срезана плоскостью (рис. 1). Можно ли полученный многогранник вписать в сферу? Зависит ли ответ на этот вопрос от того, какой именно плоскостью срезана вершина? С решением этой, а также подобных задач мы и хотим познакомить читателя.
Предположим, что нам дан выпуклый ограниченный многогранник, т. е. тело в пространстве, ограниченное со всех сторон плоскими многоугольниками — гранями — и лежащее по одну сторону от плоскости каждой из своих граней. Требуется выяснить, можно ли данный многогранник вписать в сферу.

Обозначим весь многогранник буквой
Чтобы решить поставленную задачу, надо прежде всего проверить, являются
ли все многоугольники
Задача 1. Доказать, что многогранник
Этот или аналогичный способ проверки вписанности
Первым это заметил немецкий математик Э. Штейниц. В 1927 году вышла в свет его статья, в которой была доказана следующая теорема.
Теорема Штейница. Пусть все вершины
многогранника
- Никакие две чёрные вершины не были соседними.
- Число чёрных вершин было больше, чем число белых.
Тогда многогранник
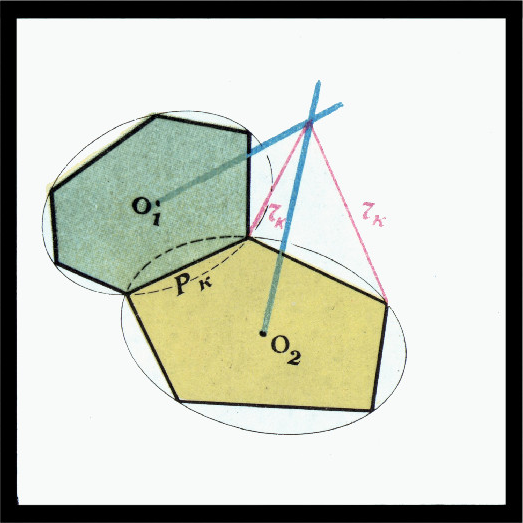
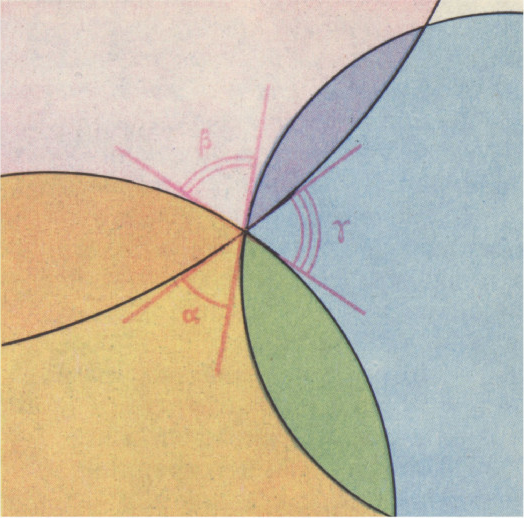
Прежде чем перейти к доказательству теоремы, сделаем некоторые замечания. Пусть у нас есть фиксированная сфера и некоторый двугранный угол, ребро которого эту сферу пересекает. Возьмём точку пересечения ребра со сферой и проведём через неё касательную плоскость (рис. 3). Двугранный угол высекает в этой плоскости линейный угол. Этот угол мы назовём линейным углом двугранного угла относительно данной сферы или просто относительным углом дву гранного угла. Очевидно, что относительный угол не зависит от выбора одной из двух точек пересечения ребра со сферой. Если же ребро касается сферы, то удобно положить величину относительного угла равной нулю.


Рассмотрим теперь выпуклый многогранный угол, все рёбра которого
пересекают данную сферу. Относительные углы его двугранных углов назовём
относительными углами данного многогранного угла. Пусть у многогранного угла
Перейдём к доказательству самой теоремы. Предположим, что многогранник
Из доказанного выше следует, что сумма относительных углов при вершине
Прежде чем переходить к анализу полученного результата, т. е. прежде чем выяснять, чем замечательна и что означает теорема Штейница, надо показать,
что теорема содержательна, т. е. что существуют многогранники,
удовлетворяющие её условиям. Возьмём октаэдр (рис. 5, а)
и на каждой его грани, как на основании, построим правильную треугольную
пирамиду, причём высоту пирамиды возьмём такой маленькой, чтобы двугранные
углы при основании были меньше


Задача 2. Доказать, что мноеогранник
Объявим белыми те его вершины, которые были вершинами исходного октаэдра, а чёрными — все остальные. Ясно, что условия теоремы Штейница выполняются. Итак, мы построили пример многогранника, которыи нельзя вписать в сферу, в чём можно убедиться, не зная ни размеров, ни углов многогранника, но зная только его строение.
Уточним, что значит строение. Начнём с плоскости. Чтобы описать строение выпуклого многоугольника, надо сказать, сколько у него вершин, тогда у него столько же и сторон; каждая сторона смежна с двумя другими, и в каждой вершине сходятся две стороны.

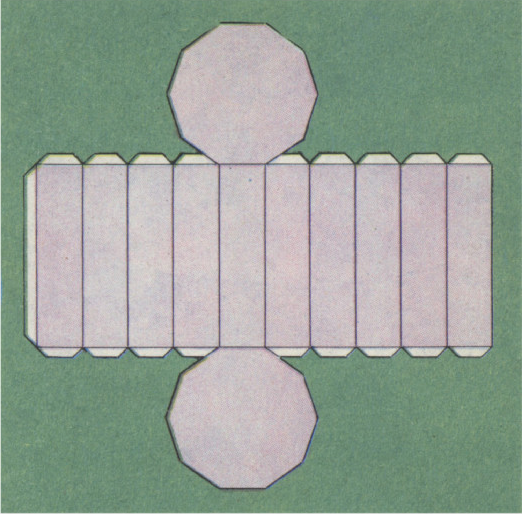
Иное дело в пространстве: у додекаэдра (рис. 6, а) и у десятиугольной призмы (рис. 6, б) одинаковое число граней — 12, одинаковое число рёбер — 30, одинаковое число вершин — 20, а строение совсем разное. В пространстве, чтобы описать строение многогранника, надо сказать не только сколько у него рёбер, граней и вершин, но и как грани склеены между собой, т. е. какие грани являются смежными, какие вершины являются соседними и какие грани сходятся в каждой из вершин. Два многогранника имеют одинаковое строение, если у них одинаковое число вершин, рёбер и граней и они одинаково из этих элементов составлены.
Назовём выпуклый многогранник
У нас есть условие Штейница — достаточное условие абсолютной невписываемости. Может быть оно является необходимым? Нет. Это вытекает из следующих задач.
Задача 3. Пусть все вершины многогранника
- Число белых было не больше числа чёрных.
- Никакие две чёрные вершины не были бы соседними и, напротив, нашлись бы две соседние белые вершины.
Доказать, что многогранник
Задача 4. Построить пример многогранника, удовлетворяющего условию задачи 3 и не удовлетворяющего условиям теоремы Штейница.
Важно отметить и другое: если в каждой вершине многогранника M сходится
одно и то же число, скажем,
Если
Остановимся теперь на многогранниках, в каждой вершине которых сходятся три грани: эти многогранники в некотором смысле самые типичные, но мы о них ничего не знаем с точки зрения их вписываемости.
Рассмотрим три попарно пересекающиеся плоскости; они либо образуют
трёхгранный угол, либо линии их пересечения параллельны; в этом случае
скажем, что они образуют бесконечный трёхгранный угол. Фиксируем некоторую
сферу. Пусть все рёбра трёхгранного угла её пересекают, а вершина этой сфере
не принадлежит, а может быть, вершины и вовсе нет. Оказывается, что если
вершина угла лежит внутри шара, но не на сфере, то сумма относительных углов
больше
Пусть все вершины многогранника
Задача 5. Пусть во всех вершинах многогранника
Задача 6. Доказать, что вершины многогранника можно разбить на чёрные и белые так, чтобы никакие две вершины одного цвета не были соседними тогда и только тогда, когда у каждой грани многогранника чётное число сторон.
Указание. Для доказательства достаточно взять любую вершину и объявить её белой, соседние с ней — чёрными и т. д. Нужно доказать, что при этом не возникает противоречий, т. е. что во всякой замкнутой ломаной, составленной из рёбер многогранника, чётное число звеньев.
Вернёмся к многограннику
Предположим, что многогранник
Точно такое же рассуждение можно провести, если отмеченные вершины срезать не одной, а несколькими плоскостями, лишь бы сходящиеся в них грани оставались попарно смежными и не сходились в одной вершине.
Этим способом можно получать и другие достаточные условия. Сейчас стали известны и некоторые необходимые условия того, чтобы многогранник был абсолютно невписываемым, но в целом проблема до сих пор не решена.
Метод относительных углов позволяет решать и другие интересные задачи.
Задача 7. Пусть в каждой вершине многогранника
Указание. Воспользоваться задачей 6. Не пропускать такой неприятной возможности: рёбра, исходящие из вершины, не лежащей на сфере, касаются сферы.
Аналогичная, но более сложная.
Задача 8. Пусть все вершины многогранника
Таким образом, если вершины можно разбить на чёрные и белые, как это описано в задаче 5, то либо многогранник абсолютно невписываемый, либо удовлетворяет задаче 8, т. е. из того, что на сфере лежат все его вершины, кроме одной, следует, что он вписанный.
Простейшим примером абсолютно невписываемого многогранника является куб с одной срезанной вершиной (см. рис. 1).
В заключение остаётся сознаться, что Штейниц доказал отнюдь не ту теорему, которая называется его именем, но двойственное к ней утверждение, которое мы сформулируем в виде задачи.
Задача 9. Пусть все грани многогранника
- Число чёрных граней было больше, чем число белых.
- Никакие две чёрные грани смежными не являются.
Доказать, что многогранник

На рисунке 8 изображён один из самых простых примеров абсолютно неописываемого многогранника — куб, у которого срезаны все вершины.
Ответы, указания, решения
Покажем, что из каждой грани произвольного выпуклого многогранника можно пройти в любую другую, двигаясь от смежной грани в смежную. Возьмём для этого две произвольные грани и выберем в них по точке, не лежащей на границе. Соединим выбранные точки отрезком. Этот отрезок не пересекает плоскостей граней многогранника, ибо многогранник выпуклый. Проведём через этот отрезок плоскость, не содержащую вершин многогранника: это возможно, так как у многогранника лишь конечное число вершин. Проведённая плоскость высекает на поверхности многогранника две ломаные. Они не проходят через вершины многогранника, т. е., двигаясь по ним, мы будем переходить от одной смежной грани к другой и пройдём из первой грани во вторую. Теперь фиксируем некоторую грань многогранника, скажем
$\textit{Г}_1$, и две точки$O_1$ и$O_2$, удалённые на$r_k$ от всех её вершин. Предположим для простоты, что во всех вершинах многогранника сходятся по три грани; в общем случае суть дела остаётся неизменной. Вершины всякой смежной с$\textit{Г}_1$ грани удалены на$r_k$ либо от$O_1$, либо от$O_2$, но не от обеих сразу, ибо все точки, равноудалённые от$O_1$ и$O_2$, лежат в плоскости грани$\textit{Г}_1$. Предположим, что найдутся такие грани$\textit{Г}_2$ и$\textit{Г}_3$, что вершины первой лежат на расстоянии$r_k$ от$O_1$, а вершины второй — от$O_2$. Ясно, что тогда найдутся две такие грани, сходящиеся в одной вершине, а значит, в силу дополнительного предположения, смежные. Тогда второй конец их общего ребра равноудалён от$O_2$ и$O_1$, что противоречит выпуклости многогранника.Итак, вершины всех смежных с
$\textit{Г}_1$ граней равноудалены от одной точки, например,$O_1$. Это верно и для вершин граней, смежных с$\textit{Г}_2$ или$\textit{Г}_3$ и т. д., т. е. для всех вершин многогранника. Обратное утверждение очевидно.- Покажем, что если все двугранные углы построенного
многогранника меньше
$\pi$, то он выпуклый. Возьмём плоскость некоторой его грани. Все смежные с ней грани лежат по одну сторону от этой плоскости, значит, по ту же сторону лежит вся треугольная пирамида, содержащая продолженную грань, и три другие пирамиды, имеющие с первой по общему ребру. Следовательно, по ту же сторону лежат две грани октаэдра, содержащие одно из рёбер первой грани, а значит, и сам октаэдр и остальные пирамиды. Чтобы завершить доказательство, достаточно вычислить двугранный угол октаэдра. - Действуя, как при доказательстве теоремы Штейница, легко заметить, что сумма в первой части строго больше 0 (а не больше либо равна как в теореме), зато в левой части сумма меньше либо равна 0 (а не строго меньше 0).
- В примере, построенном к теореме Штейница, надо подклеить лишь часть пирамид.
- Доказательство в точности совпадает с доказательством того, что если в каждой вершине многогранника сходится
$k$ граней, то он заведомо не удовлетворяет теореме Штейница. Покажем, что всякая замкнутая ломаная, составленная из рёбер многогранника — чётнозвенная. Ясно, что это достаточно доказать для ломаных без самопересечения.
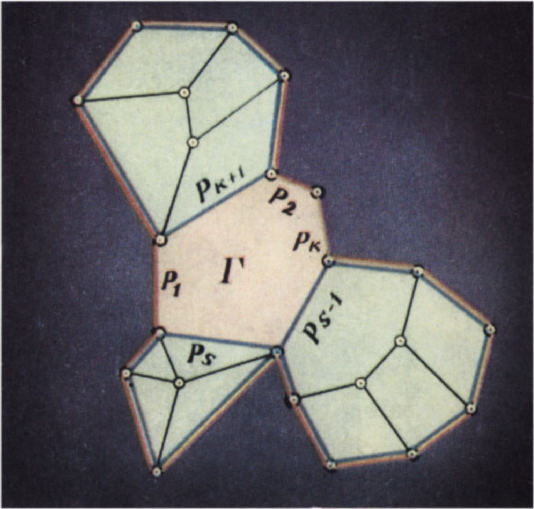
Рассмотрим некоторую ломаную, не содержащую самопересечений и разрежем многогранник по этой ломаной. Пусть в одной части
$K$ граней, а в другой$L$ и$L\le K$. Целое число$L$ назовём обхватом ломаной. Если обхват равен 1, то доказываемое утверждение следует из условия задачи. Применим индукцию, пусть для ломаных обхвата меньше$L$ задача решена. Выберем грань$\textit{Г}$, ребро которой принадлежит ломаной и которая лежит в той части многогранника, где граней меньше. Пусть$\textit{Р}_1$, $\textit{Р}_2$, $\ldots$, $\textit{Р}_k$ — рёбра ломаной, являющиеся рёбрами грани$\textit{Г}$ и$\textit{Р}_{k+1}$, $\ldots$, $\textit{Р}_s$ — остальные рёбра грани$\textit{Г}$. Перейдём к новой ломаной, которая получается из исходной заменой рёбер$\textit{Р}_1$, $\ldots$, $\textit{Р}_k$ на$\textit{Р}_{k+1}$, $\ldots$, $\textit{Р}_s$. Возможно, новая ломаная с самопересечениями и даже состоит из нескольких несвязанных кусков, но обхват каждой её несамопересекающейся части заведо мо меньше$L$, значит, новая ломаная чётнозвенная. Предположим, что в ней$2N$ звеньев. У выбранной в начале доказательства грани$2Q=s$ сторон, тогда число звеньев исходной ломаной равно$2N+2Q-2K$ — чётное число (рис. 1).Мы изложим решение задачи 8, из которой задача 7 легко следует. Рассмотрим
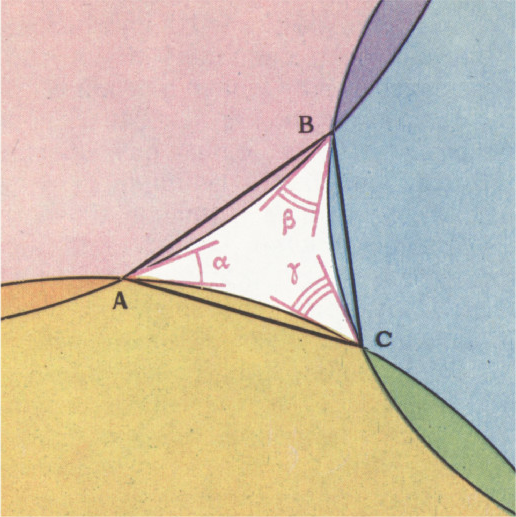
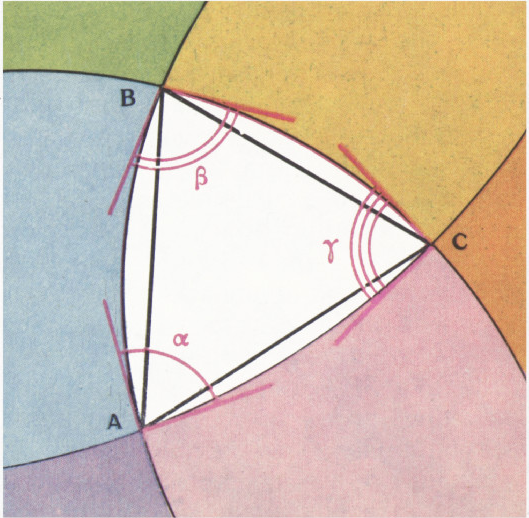
$k$ -гранный угол, вершина которого не лежит на сфере. Проведём луч$l$, целиком содержащийся внутри (но не на границе) угла. Пусть вначале вершина лежит вне шара. Каждая окружность разбивает сферу на две «шляпки». Рассмотрим окружности — пересечения граней угла со сферой и выберем для каждой из них ту шляпку, которая не содержит точек$A$ и$\textit{В}$ — точек пересечения луча$l$ со сферой. Рассмотрим стереографическую проекцию на плоскость с центром проекции в точке$A$. Фиксированные$k$ шляпок не пересекаются в одной точке, значит, при проекции возникнет такая картина, как на рисунке 2.$\textit{В}'$ — образ точки$\textit{В}$ при проекции. Сумма углов многоугольника$A_1$, $\ldots$, $A_k$ строго больше суммы относительных углов. Мы не знаем, является ли он выпуклым, но ясно, что прямые отрезки, соединяющие точку$\textit{В}'$ с точками$A_i$, ему целиком принадлежат. Это следует из определения луча$l$. В силу этого$\angle A_1+\ldots+\angle A_k=\pi(k-2)$ и сумма относительных углов меньше$\pi(k-2)$. 
Рис. 2 Если вершина лежит внутри шара, то совершенно аналогично доказываем, что сумма относительных углов больше
$\pi(k-2)$. Перейдём непосредственно к решению зaдачи. Пусть
$\textit{В}_1$ — вершина, положение которой не определено. Разобьём вершины, как это описано в задаче 6, на чёрные и белые. Пусть$\textit{В}_1$ — белая. Нетрудно видеть, что если вершина$k$ -гранного угла лежит на сфере и все его рёбра сферу пересекают, кроме одного ребра, касательного к сфере, то сумма относительных углов равна$\pi(k-2)$. Теперь перейдём к внешним относительным углам и вычислим их суммы при каждой вершине. При всех вершинах, кроме
$\textit{В}_1$, эти суммы заведомо равны$2\pi$. Если$\textit{В}_1$ не лежит на сфере, то сумма при ней не равна$2\pi$. Сложим равенства при белых вершинах, вычтем из них равенства при чёрных и в итоге получим, что$0\ne0$. Таким образом,$\textit{В}_1$ лежит на сфере.Предположим противное. Соединим точку касания каждой грани с вершинами грани отрезками и рассмотрим угол между двумя отрезками, который опирается на некоторое ребро многогранника (рис. 3). Величина этого угла не зависит от выбора одной из граней, содержащих ребро.
$\triangle O'\textit{В}_1\textit{В}_2=\triangle O''\textit{В}_1\textit{В}_2$ (по трём сторонам), значит,$\angle \textit{В}_1O'\textit{В}_2=\angle \textit{В}_1O''\textit{В}_2$. 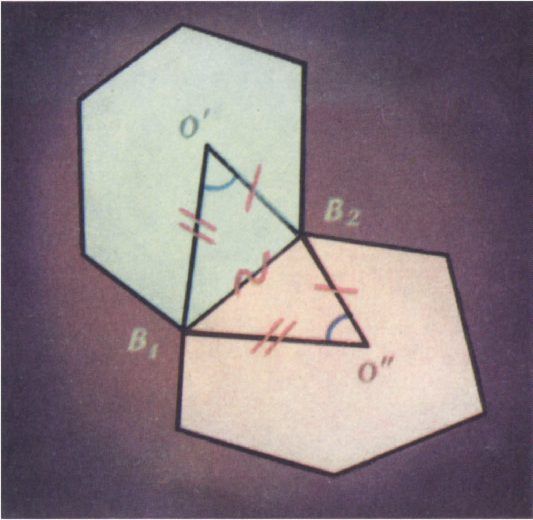
Рис. 3 Припишем каждому ребру величину угла, на него опирающегося. Обозначим угол, приписанный ребру
$\textit{Р}_k$, через$\beta_k$. Сумма углов, приписанных рёбрам каждой грани, равна$2\pi$. Дальнейшее доказательство получается из доказательства теоремы Штейница заменой слова вершина на слово грань.