Виленкин Н. Я.

Тайны бесконечностиВиленкин Н. Я. Тайны бесконечности : [Зенон, Демокрит, Архимед] // Квант. — 1970. — № 3. — С. 2‍—‍13.‍‍

Мгновение вечности

Интерес к очень большим числам появился в самой глубокой древности. Египтяне, чтобы сказать о чём-то, что очень велико, прибегали к образным сравнениям. В тексте одной гробницы жреца бога Аи (XIV век до н. э.) говорится:

«Да наградит тебя он (бог) юбилеями как число песку берега моря, измеряемого жезлом ипет, как мера моря, определяемая джауэтом, или вес горы, взвешенной на весах, или перья птиц, или листья деревьев».

Египтянам было трудно выразить иначе свою мысль, так как они не развили в достаточной мере систему числовых обозначений. Но ещё около 5000 лет тому назад в Древнем Вавилоне появилась шестидесятеричная система счисления‍, и вавилонские математики свободно справлялись с весьма большими числами. В одной из древневавилонских таблиц приводятся, например, все делители числа $60^8+10\cdot60^7=195\,955\,200\,000\,000$‍.‍

Об очень больших числах говорится и в индийских легендах о Будде. По одной из них, его ещё в детстве подвергли испытанию в числах, и, переходя от одного разряда к другому, он дошёл до чисел, которыми выражается число песчинок десятка лакх рек ($\text{лакха}=100\,000$‍)‍ таких, как Ганг. А затем пошли ещё бо́льшие числа и, наконец, число, «при помощи которого боги исчисляют своё прошедшее и будущее». А в другой индийской легенде рассказывается о сражении, в котором участвовало $10^{23}$‍‍ обезьян. Такое количество обезьян не поместилось бы не только на поверхности Земли, но и во всей Солнечной системе, даже если всю её набить битком обезьянами!

По-видимому, уже египтяне и вавилоняне пришли к идее вечности — к мысли, что течение времени не будет иметь конца, Эта идея ярко выражена в восточной притче:

«Вот алмазная гора высотой в тысячу локтей. Раз в столетие прилетает птичка и точит свой клюв о гору. Когда она сточит всю гору, пройдёт первое мгновение вечности».

Исчисление песчинок

И в Египте и в Индии пользовались одним и тем же символом гигантского числа — количеством песчинок на берегу реки или моря. Число это, конечно, очень велико. Если даже считать, что объём одной песчинки — 1 кубический миллиметр (на самом деле она ещё меньше), то в одном кубическом метре песка содержится миллиард песчинок, а в одном кубическом километре песка их миллиард миллиардов! Человек, отсчитывающий по две песчинки в секунду и занимающийся этим делом каждый день по 10 часов в течение 80 лет, отсчитал бы нe более трёх миллиардов песчинок. Поэтому опровергнуть прямым опытом мысль, что количество песчинок неисчислимо, было бы весьма затруднительно. Во всяком случае, чисел, которые содержатся в вавилонских табличках, для этого недостаточно.

Чтобы назвать число, превосходящее количество песчинок как в странах населённых, так и необитаемых, надо было дальше развить систму счисления, систему записи чисел. Эту задачу решил великий математик древности Архимед, родившийся, как полагают, в 287 году до нашей эры и убитый при взятии его родного города Сиракузы — в 212 году до нашей эры. Архимеду мы обязаны многими открытиями в физике и математике, развитие которых привело впоследствии к созданию интегрального исчисления, гидростатики и других наук. Его имя может служить символом величайшей математической одарённости. Многие сочинения Архимеда не дошли до нашего времени. В частности, утрачена работа Архимеда арифметического характера. Но, к счастью, сохранилась книга, в которой он развивает свою систему счисления. Она называется «Псаммит», или «Исчисление песчинок в пространстве, равном шару неподвижных звёзд».

Ещё до Архимеда греки пользовались десятичной системой счисления и доходили до тысячи мириад, т. е. до $10\,000\,000$‍.‍ Архимед начинает счёт с мириады мириад‍, т. е. с $100\,000\,000$‍.‍ Это число он называет октадой‍ или единицей чисел вторых. Потом идёт октада октад, которую он назвал единицей чисел третьих. Наконец, он доходит до октад чисел октадных, т. е. до числа, равного единице с 800 миллионами нулей. Это число он объявил единицей второго периода. Кончил Архимед свою систему октадой чисел октадных октадного периода, т. е. числом $10^{8\cdot10^{16}}$‍.‍ Если написать это число, записывая 400 цифр на полоске длиной в 1 метр, то получится лента такой длины, что ею можно будет опоясать земной экватор примерно 5000 раз. Даже на ракете, делающей по 8 км в секунду, пришлось бы лететь около 300 дней, чтобы пролететь вдоль всей ленты.

И хотя ещё до Архимеда учёные знали, что количество натуральных чисел бесконечно, что последнего натурального числа не существует, только после «Псаммита» возможность называть числа, превосходящие не только количество песчинок на берегу моря, но и число песчинок в «шаре неподвижных звёзд»; — как показал Архимед, оно меньше тысячи мириад чисел восьмых, т. е. меньше, чем $10^{63}$‍.‍ Идея бесконечного числового ряда, математическая модель, отражавшая вечность времени, как бы материализовалась в октадах и периодах исчисления Архимеда.

Бесконечные миры в бесконечной Вселенной

Таким образом, идея бесконечности впервые возникла как идея вечности, идея неограниченного во времени существования мира. Однако и в Египте и в Вавилоне не было ещё, по-видимому, мысли о бесконечности пространства. Вселенная считалась ограниченной твёрдой сферой, опирающейся на Землю, а за пределами этой сферы не было ничего, доступного пониманию смертных. Но уже в VI веке до н. э. в Древней Греции возникла идея бесконечности пространства. Философ Анаксимандр впервые высказал догадку о бесконечности миров в бесконечной Вселенной. Греческие философы говорили: «Где бы ни стал воин, он сможет протянуть своё копьё ещё дальше»‍.

Так возникла модель мира, бесконечного по всех направлениях и вечного во времени. Наиболее смелые мыслители утверждали даже, что мир не имел и начала, но их преследовали как безбожников, отрицающих создание мира богами.

Делится или не делится?

Итак, устройство Вселенной «в большом» было выяснено (или по крайней мере казалось, что оно выяснено). Но одновременно с этим философы и математики размышляли и о том, из чего состоит весь видимый мир, как он устроен «в малом». Повседневный опыт учил, что ковригу хлеба, окорок кабана, кувшин вина можно разделить между сидящими за столом. В случае необходимости можно было каждую из частей разделить снова на части. Но если продолжить это деление, то рано или поздно наступит момент, когда части получатся настолько малыми, что дальше их делить окажется уже практически невозможным. Для того чтобы выразить такие малые «неделимые» величины, уже издавна применялись образы «пылинки», «макового зерна» и т. д. Но если маковое зерно можно всё же, хоть и с трудом, разделить на части, то можно ли делить на части пылинку, пляшущую в солнечном луче? На этот вопрос повседневный опыт ответа не давал, и приходилось опираться только на рассуждения, проводить чисто умозрительный анализ.

Один из дошедших до нас ответов на этот вопрос принадлежал жившему в V веке до н. э. греческому философу Анаксагору. Он учил:

«Среди малых величин не существует наименьшей, но уменьшение идёт непрерывно, ибо существующее не может перестать существовать».

Он же говорил:

«Все вещи (в начале мироздания) были вместе, они бесконечно многочисленны и бесконечно малы».

Итак, по Анаксагору, всё состояло из бесконечного множества бесконечно малых частей. При этом, конечно, лод бесконечно малой понималась не переменная, стремящаяся к нулю, как это принято сейчас в математике, а не имеющая размеров точка.

Но это противоречило двум основным аксиомам, общепринятым в греческой математике. Греческие учёные разделяли все величины на протяжённые и непротяжённые. При этом они считали, что:

1. Сумма бесконечно большого числа любых, хотя бы и очень малых протяжённых величин обязательно должна быть бесконечно большой.
2. Сумма любого, хотя бы и бесконечно большого числа непротяжённых величин всегда равна нулю и никогда не может быть равной некоторой заранее заданной протяжённой величине.

Получалось, что бесконечно малые, из которых, по Анаксагору, был составлен мир, не могли быть ни протяжёнными, ни непротяжёнными, т. е. они не могли существовать.

Против идеи бесконечной делимости выдвигались и иные возражения. Через много столетий после Анаксагора Плутарх писал:

«Если деление двух величин на части может продолжаться до бесконечности, то нет основания считать одну величину больше, чем другая, а самая природа неравенства уничтожается».

Смысл этого возражения в том, что после деления обе величины окажутся составленными из одного и того же (бесконечного) числа одинаковых (бесконечно малых) величин.

Неподвижный мир

Пожалуй, самые сильные доводы против идеи бесконечной делимости выдвинул философ Зенон Элейский, живший в Италии в середине V века до н. э. Он «показал», что допущение бесконечного деления приводит... к отрицанию возможности движения. Свои рассуждения Зенон облёк в весьма живую, парадоксальную форму. Так, в одном из них он «доказывает», что быстроногий Ахиллес никогда не догонит медленную черепаху — ведь сначала он должен достичь точки $A$‍,‍ откуда поползла черепаха, потом точки, где она окажется в момент, когда Ахиллес достиг точки $A$‍,‍ и т. д. По тем же «соображениям» вообще нет движения, потому что движущееся тело сначала должно достичь середины пути, а до этого — четверти и т. д., так что движение никогда не начнётся.

Разумеется, Зенон не «доказал», что мир неподвижен — этому противоречил повседневный опыт. Но он показал, что модели мира, которые строили до него философы и математики, были неудовлетворительными с точки зрения логики, что нужна была серьёзная перестройка взглядов на устройство мира «в малом». Как отметил В. И. Ленин, «философское значение апорий‍ Зенона состояло в том, что они вскрыли действительную противоречивость движения, пространства и времени».

Атомы и амеры

Вызов Зенона принял один из крупнейших философов (и, по-видимому, математиков) древности Демокрит из Абдеры, один из создателей научного атомизма. К сожалению, до нас не дошли подлинные работы Демокрита. Он был убеждённым материалистом, и временно восторжествовавшая школа идеалиста Платона вела жестокую борьбу с учением Демокрита. Рассказывают даже, что Платон скупал рукописи Демокрита и сжигал их. Стоили тогда рукописи дорого, каждое сочинение писалось в малом числе экземпляров, так что, если этот рассказ верен, неудивительно, что до нас ни одна рукопись Демокрита не дошла. А может быть, просто средневековые монахи, занятые переписыванием многочисленных трудов Платона и Аристотеля, не трогали пожелтевших папирусов с трудами Демокрита, рукописи ветшали, приходили в негодность и выбрасывались. Один из основателей современного естествознания Бэкон Веруламский сказал:

«Но что касается более древних из греческих учёных — Эмпедокла, Анаксагора, Левкиппа, Демокрита, то их произведения были уничтожены в потоке времени. Ведь время как река: более лёгкое и пустое внутри оно донесло до нашего времени, более тяжкое и веское погрузило на дно».

И теперь нам приходится выискивать ссылки на труды Демокрита в работах его противников, искать в их книгах цитаты, которые, по-видимому, принадлежат Демокриту, изучать дошедшие до нас труды его немногочисленных последователей — Лукреция Кара и других. Неудивительно, что среди учёных нет единства по истолкованию учения Демокрита, что одни и те же цитаты толкуются по-разному.

Весьма убедительное истолкование учения Демокрита дал советский историк науки С. Я. Лурье. По его мнению, Демокрит считал, что все тела состоят из неделимых далее частиц. Но при этом он различал неделимые частицы двух видов — атомы и амеры. Атомы — это сплошные частицы материи, имеющие самую разнообразную форму и размеры (Демокрит говорил даже об атомах величиной с наш мир!), но далее уже неделимые ввиду отсутствия в них пустот и крайней их твёрдости. Но мысленно атомы можно делить и далее. Однако и этому мысленному делению наступает конец — атомы делятся на мельчайшие частицы, имеющие минимальное протяжение, — на амеры. У амеры нет ни формы, ни верха, ни низа, ни середины, она неделима даже в воображении. Но в то же время амеры не являются точками. Таким образом, по сути дела, Демокрит выдвинул идею о существовании минимальной длины, вновь возникающую сейчас у некоторых физиков-теоретиков.

Из нескольких амер, идущих одна за другой, получаются линии, из рядом расположенных линий — поверхности, а из поверхностей — тела. Таким образом, Демокрит изучал материальные линии (имеющие минимальную ширину) и материальные поверхности (имеющие минимальную толщину). Например, конус, по Демокриту, состоял из кружков, имевших минимальную толщину, а пирамида — из таких же многоугольников. Шар он представлял себе состоящим из иголочек-пирамид, вершины которых находятся в центре шара. Аристотель писал:

«По Демокриту, и шар режет, так как и он угловат».

Такой подход позволил Демокриту решить многие проблемы, стоявшие перед геометрами. Так, он был первым, вычислившим объём конуса и пирамиды, он первым свёл вычисление объёма шара к вычислению площади сферы. С пирамидой он справился, по-видимому, так.

Сначала он доказал теорему, что две пирамиды, имеющие равновеликие основания и равные высоты, имеют один и тот же объём. Здесь для него не было никаких осложнений — пирамиды с одинаковой высотой состояли, по Демокриту, из равного числа соответствующих треугольников, причём их объёмы были суммами «объёмов» треугольников (ведь, по Демокриту, треугольники были материальными, имели минимальную толщину). Поскольку площади оснований обеих пирамид были одинаковы, то «объёмы» соответствующих треугольников в обеих пнрамидах совпадали, и потому совпадали и объёмы пирамид. А потом он делил трёхгранную призму на три пирамиды, имеющие попарно одну и ту же высоту и равновеликие основания (см. рисунок). Таким путём Демокрит «доказывал», что объём пирамиды равен одной трети объёма призмы, имеющей ту же высоту и то же основание. А равенство объёмов пирамиды и конуса, имеющего ту же высоту и то же по площади основание, доказывалось уже совсем просто — они состояли из одинакового количества фигур одного и того же «объёма».

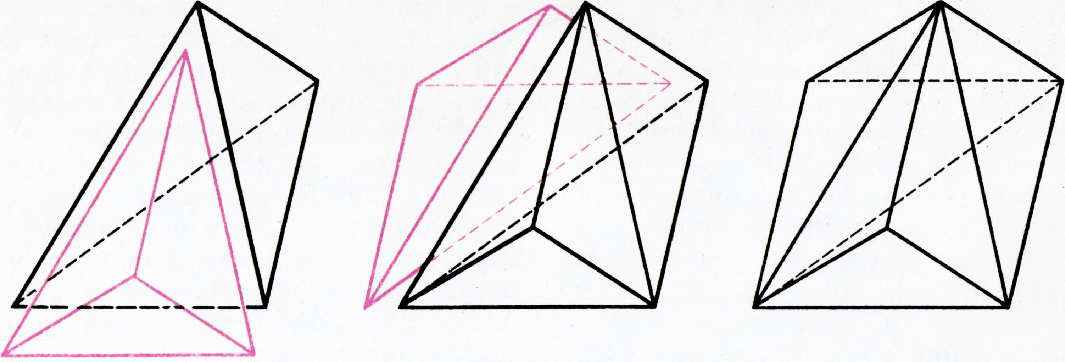
Ясно и то, как подходил Демокрит к задаче об объёме шара. Раз шар состоит из иголочек-пирамид, то объём шара равен сумме объёмов этих пирамид. А объём каждой пирамиды он уже умел находить. Суммируя эти объёмы, он пришёл к ответу: «Объём шара равен одной трети произведения радиуса шара на площадь поверхности шара». Вычислить эту площадь ему не удалось.

Шершавая пирамида

Демокрит добился замечательных результатов определения объёмов геометрических тел. Но большинство современников отвергло его методы. Слишком непохожими были идеи Демокрита на результаты непосредственного опыта. Ведь даже деление отрезка пополам было в геометрии Демокрита весьма сложной проблемой. Отрезок, состоящий из нечётного числа неделимых, нельзя было разделить пополам: средняя неделимая должна была отойти к одной из половин, и эта половина становилась больше, чем другая. Невозможно было разделить пополам и круг: при таком делении диаметр круга отходил к одной из половин, делая её больше, чем другая. Мало того, по Демокриту, и прямые и окружности состояли из неделимых одного и того же вида. Поэтому окружность и касавшаяся её прямая имели общую неделимую, общую амеру. Следовательно, к окружности можно было провести лишь конечное число касательных.

Да и пирамида, принёсшая столь большой успех Демокриту, получалась у него какой-то странной. Ведь надо было решить вопрос, равны ли друг другу параллельные сечения пирамиды. Если они равны, то пирамида не сужается к вершине, а если различны, то пирамида имеет ступенчатую форму (такую, какую имеют египетские пирамиды).

По-видимому, Демокриту не удалось построить непротиворечивую геометрию, хотя его геометрия не была столь наивной, как рисуют его противники. Во всяком случае, один из самых замечательных результатов предшественников Демокрита — существование несоизмеримых отрезков — не находил объяснения в его построениях: по Демокриту, все отрезки должны были быть соизмеримыми, измеряться минимальной длиной. И геометры отвергли идеи Демокрита, вместо материальных поверхностей стали рассматривать идеальные, не имеющие толщины, вместо материальных линий — идеальные, а вместо амер — точки, не имеющие длины. Правда, при делении отрезка пополам всё равно приходилось удваивать делящую точку, но это было уже неважно: размеров она не имела и на длину влияния оказать не могла.

Сам Аристотель поучал, что «введение минимальной длины расшатывает самые великие основы математики». Как говорил верный последователь Аристотеля средневековый схоластик Фома Брадварин, «все научные системы истинны лишь постольку, поскольку они не основаны на предположении, что непрерывное состоит из неделимых». И ещё в XVII веке парижский парламент пригрозил смертной казнью всем противникам мнений Аристотеля. А в частности — всем сторонникам атомизма.

Метод истощения

Итак, математикам пришлось отвергнуть и метод неделимых Демокрита и бесконечные процессы — критика Зенона подорвала всякое доверие к результатам, полученным путём использования понятия бесконечности. В результате возникло трудное положение — методы Демокрита, хотя и путём нестрогих рассуждений, давали правильные формулы для вычисления площадей и объёмов; теперь же приходилось разрабатывать новую процедуру вычисления геометрических величин, в которой ни звука не говорилось бы ни о бесконечности, ни о бесконечно малых, ни о неделимых. Такую процедуру создал в IV в. до н. э. предшественник Евклида математик Евдокс, разработавший «метод исчерпывания» (или, иначе, «истощения»), в котором многие видят предка современного метода пределов. Этим методом широко пользовался Евклид в своих «Началах».

Например, вот как Евклид доказывает, что площади двух кругов относятся, как квадраты их диаметров $$ \dfrac{S_1}{S_2}=\dfrac{d_1^2}{d_2^2}. $$ Пусть это неверно. Тогда $\dfrac{d_1^2}{d_2^2}=\dfrac{S_1}S$‍,‍ где $S$‍‍ либо меньше, либо больше $S_2$‍.‍

Допустим сперва, что $S\lt S_2$‍.‍ Впишем в круг с диаметром $d_2$‍,‍ квадрат и будем строить правильные вписанные многоугольники, последовательно удваивая число сторон. Легко доказать, что через несколько шагов разность между площадью круга и площадью $P_2$‍‍ вписанного многоугольника станет меньше, чем $S_2-S$‍,‍ т. е. $S_2-P_2\lt S_2-_S$‍,‍ а значит, $P_2\gt S$‍.‍ А теперь впишем в круг с диаметром $d_1$‍,‍ многоугольник, подобный вписанному в круг с диаметром $d_2$‍;‍ площадь этого многоугольника обозначим через $P_1$‍.‍ Так как площади подобных правильных многоугольников относятся, как квадраты диаметров описанных кругов, то $$ \dfrac{P_1}{P_2}=\dfrac{d_1^2}{d_2^2}. $$ Но мы допустили, что $\dfrac{d_1^2}{d_2^2}=\dfrac{S_1}S$‍,‍ a потому $$ \dfrac{P_1}{P_2}=\dfrac{S_1}S $$ или, в силу свойств пропорций, $$ \dfrac{P_1}{S_1}=\dfrac{P_2}S.\tag{*} $$ Но $P_1\lt S_1$‍‍ (площадь вписанного многоугольника меньше площади круга), a $P_2$‍,‍ как только что было показано, больше $S$‍.‍ Итак, левая часть равенства (*) меньше единицы, а правая — больше единицы, что абсурдно. Значит, неравенство $S\lt S_2$‍‍ невозможно.

Точно так же доказывается, что невозможно неравенство $S\gt S_2$‍‍ (проведите доказательство сами!).

Итак, предположения $S\lt S_2$‍,‍ $S\gt S_2$‍,‍ опровергнуты и остаётся единственная возможность: $S=S_2$‍,‍ т. е. $$ \dfrac{d_1^2}{d_2^2}=\dfrac{S_1}{S_2}. $$

Но если для круга и результат можно было легко угадать, и рассуждения были не слишком сложны, то вычисление объёма конуса или пирамиды методом истощения было делом сложным и запутанным. Впрочем, с конусом и пирамидой можно было ещё справиться — ведь ответ был известен со времён Демокрита, и Евдоксу пришлось лишь уточнить соображения Демокрита, заменив разбиение пирамиды на неделимые далее треугольники рассуждениями по методу истощения.

Но когда надо было искать объёмы фигур, с которыми Демокрит дела не имел, например эллипсоида вращения или параболаида вращения, дело было совсем плохо — неизвестно было, для какой величины доказывать, что объём не может быть ни больше, ни меньше этой величины. Иными словами, метод истощения мог служить только для доказательства уже найденных результатов, но не для открытия новых.

И лень бывает полезна

Впрочем, математики, жившие после Евдокса, не слишком стремились к открытию новых формул. Центр научной мысли переместился в это время из Греции в Египет, где под опекой Птоломеев в Александрийском музее учёные изучали небо, приводили в систему ранее накопленные математические знания, писали оды в честь высоких покровителей наук, переписывали древние рукописи. Надо сказать, что сделали александрийские учёные не так уж мало, только работы их носили скорее эпигонский характер. Они больше разрабатывали ранее достигнутое, чем пролагали новые пути.

Одним из немногих исключений в тихой семье александрийских учёных был приехавший учиться из далёких Сиракуз родственник сиракузского царя Архимед. В отличие от большинства тогдашних учёных, он интересовался не только высокой теорией, но и практическими приложениями науки, изобрёл винтовой насос, которым потом пользовались много столетий, делал механические игрушки, а впоследствии, когда его родной город осадили римляне, строил военные машины. Понятно, что Архимед весьма заинтересовался механикой, равновесием рычагов, плаванием тел и т. д. А механика была ещё со времён Платона отлучена от чистой науки и считалась чем-то родственным ремеслу. Поэтому в механике не слишком тщательно следили за строгостью рассуждений, и механики широко использовали в своих исследованиях атомистику, расщепляя мысленно клинья на атомы-клинья, имеющие общую вершину с целым клином, водяные вихри — на ряд «атомных» кругов малой толщины и т. д.‍.

И во многих работах Архимеда встречается любопытное сочетание метода истощения с рассуждениями, почерпнутыми из механики. Он научился прилагать к решению геометрических задач понятия центра тяжести, рычага и получил таким путём новые результаты, недоступные тогдашней «чистой математике»‍. А поскольку результаты механики опирались в конечном счёте на атомистические рассуждения, то на самом деле Архимед в этих работах опирался на атомистику. Только явно он об этом ничего не писал. Хороший математический тон того времени, по-видимому, требовал, чтобы учёные излагали свои результаты, не ссылаясь на преданные анафеме идеи Демокрита. А может быть, Архимед тогда ещё и не читал Демокрита — на это указывают некоторые детали его работ.

Поэтому из больших работ Архимеда, дошедших до XVI‍—‍XVII веков, математики не могли узнать, ка́к он догадывался, какие результаты надо ему доказывать. Им приходилось только следовать за изгибами мысли Архимеда, лишь в самом конце убеждаясь в его правоте. Но в некоторых отрывках, цитированных Героном и другими учёными, упоминалось о каком-то послании Архимеда Эратосфену. В этом послании Архимед писал «о рассуждениях, основанных на методе, но не являющихся ещё доказательствами». Многие учёные полагали, что эти рассуждения и должны были раскрыть атомистический подтекст работ Архимеда. Но, чтобы убедиться в этом, нужно было иметь в руках полный текст послания. Как часто бывает, помог счастливый случай.

В 1906 году приват-доцент Петербургского университета Попадопуло-Керамевс нашёл в библиотеке одного из иерусалимских монастырей какой-то богословский трактат. Так как в средние века пергамент был очень дорог, то обычно брали древние книги, смывали или стирали с них языческие тексты и писали житие какого-нибудь святого мученика. Того же происхождения была и рукопись, заинтересовавшая Попадопуло. Приват-доцент был весьма слаб в математике и не слишком заинтересовался остатками смытого текста (к счастью, монах, писавший трактат; поленился и только смыл текст, а не стёр его). Он привёл лишь маленькую выдержку из древней рукописи. Ho для известного датского историка математики Гейберга этой выдержки оказалось достаточно, чтобы установить — монах смыл текст Архимеда. Среди многих работ, прочтённых Гейбергом, оказалось и послание Эратосфену.

В этом послании Архимед отдаёт должное заслугам Демокрита, говоря, что он был первым, кто установил теоремы об объёме конуса и пирамиды, не дав им, правда, должного доказательства. И метод, с помощью которого Архимед проводил предварительное исследование проблемы, оказался близким методам Демокрита. Он разлагает цилиндры, конусы и шары на чрезвычайно тонкие кружочки, доказывает нужное ему положение для одного из них, отмечает что вывод должен быть верен и для остальных и, наконец, говорит: «Так как всё тело сложено из таких кружков и целиком заполнено ими, то утверждение верно для всего тела». А ведь это почти дословно совпадает с рассуждениями атомистов!

Архимед хорошо понимал всю ценность своего метода и надеялся, что с помощью этого метода «кто-нибудь из теперешних или будущих исследователей... найдёт и другие теоремы, которые мне не пришли ещё в голову». К сожалению, послание Архимеда оказалось неизвестным именно тем математикам, которым оно было нужнее всего, — творцам исчисления бесконечно малых Кеплеру, Галилею, Кавальери. Но они по отдельным намёкам восстанавливали ход мыслей Архимеда.

Рассказ о том, ка́к возродились атомистические представления, ка́к был создан современный математический анализ; появится ещё на страницах «Кванта».

Литература

1. Б. Л. Ван дер Варден, Пробуждающаяся наука. Физматгиз, 1959.
2. М. Я. Выгодский, Арифметика и алгебра в древнем мире. Наука, 1967.
3. И. А. Гейберг, Естествознание и математика в классической древности.
4. В. Ф. Каган, Архимед. Гостехиздат, 1951.
5. C. Я. Лурье, Теория бесконечно малых у древних атомистов. Изд-во АН СССР, 1935.
6. С. Я. Лурье, Архимед. Изд-во AH CCCP, 1935.