Мордкович А. Г.

Кое-что о радикалахМордкович А. Г. Кое-что о радикалах // Квант. — 1970. — № 3. — С. 53‍—‍57.‍‍

— А теперь, — сказал Экзаменатор, — я хочу предложить Вам ещё одну задачу, весьма несложную. Вот она:

Найти стороны прямоугольного треугольника, если известно, что проекция одного катета на гипотенузу равна 6 см, а проекция другого катета на 1,5 см меньше длины этого катета.

... Через несколько минут Абитуриент бодро подошёл к Экзаменатору.

— Ну, как, решили задачу? — спросил Экзаменатор.

— Да! — ответил Абитуриент.

— И что же получилось?

— Задача не имеет решения.

— И Вы можете это доказать?

— Конечно! Рассмотрим треугольник $ABC$‍‍ (см. рисунок); $C$‍‍ — вершина прямого угла, $CH$‍‍ — высота. Пусть АС=х, тогда по условию $AH=x-1{,}5$‍,‍ а $BH=6$‍.‍

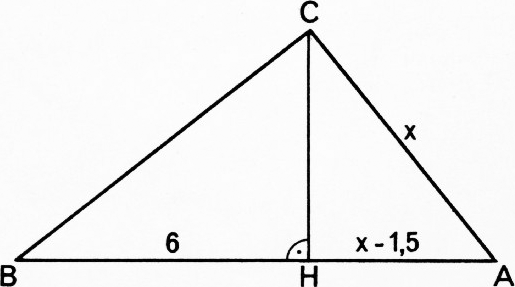
Используем известное соотношение $$ CH^2=BH\cdot AH\quad\text{или}\quad CH^2=6(x-1{,}5). $$ Применив к прямоугольному треугольнику $ACH$‍‍ теорему Пифагора, получим $$ \sqrt{AC^2-CH^2}=AH, $$ т. е. $$ \sqrt{x^2-6(x-1{,}5)}=x-1{,}5. $$

— Ну, что ж, пока всё верно, — заметил Экзаменатор, — хотя должен сказать, что путь решения выбран не самый рациональный.

— А далее, — продолжал Абитуриент, — остаются простые вычисления: $$ \begin{gather*} \sqrt{x^2-6x+9}=x-1{,}5;\quad\sqrt{(x-3)^2}=x-1{,}5;\\ x-3=x-1{,}5;\quad-3=-1{,}5. \end{gather*} $$ Так как последнее равенство неверно, то задача не имеет решения.

— К сожалению, я должен Вас разочаровать, — сказал Экзаменатор, — задача имеет решение. Её можно решить, например, так: из известного соотношения $AC^2=AB\cdot AH$‍‍ имеем $x^2=(x+4{,}5)(x-1{,}5)$‍,‍ $3x=4{,}5\cdot1{,}5$‍‍ и $x=2{,}25$‍,‍ т. е. $AC=2{,}25~\text{см}$‍.‍ Тогда $AB=6{,}75~\text{см}$‍,‍ а $BC=4\sqrt2~\text{см}$‍.‍

И, перехватив недоуменный взгляд Абитуриента, Экзаменатор добавил:

— Вас, видимо, интересует, где ошибка в Ваших рассуждениях. Ну, что ж, давайте разберёмся.

Где ошибка?

— Вы помните, — начал Экзаменатор, — что я, хотя и с оговоркой, одобрил Ваши геометрические рассуждения. Значит, ошибка могла произойти только в том, что вы назвали «простыми вычислениями». А точнее, ошибка допущена при извлечении квадратного корня. Вы не учли, что, по смыслу задачи, величина $\sqrt{(x-3)^2}$‍‍ должна быть положительной. Да и вообще, в области действительных чисел, знак $\sqrt{\vphantom1~}$‍‍ подразумевает арифметическое, неотрицательное значение корня. Так, $\sqrt{16}=4$‍,‍ и нельзя писать, что $\sqrt{16}=-4$‍‍ или $\sqrt{16}=\pm4$‍.‍ Потому нельзя утверждать, что всегда $\sqrt{a^2}=a$‍:‍ при $a\ge0$‍‍ это равенство справедливо, но ведь число $a$‍‍ может быть и отрицательным! Упростите, например, $\sqrt{(-3)^2}$‍.‍

Абитуриент написал: $$ \sqrt{(-3)^2}=\sqrt9=3. $$

— Правильно. Иными словами, $$ \sqrt{(-3)^2}=-(-3). $$ И вообще, если $a\lt0$‍,‍ то $\sqrt{a^2}=-a$‍.‍

Таким образом, $$ \sqrt{a^2}=\begin{cases} \hphantom-a,&\text{если}~a\ge0,\\ -a,&\text{если}~a\lt0. \end{cases} $$

— Я понял, — воскликнул Абитуриент, — это можно коротко записать так: $\sqrt{a^2}=|a|$‍,‍ ведь модуль $a$‍‍ определяется точно так же: $$ |a|=\begin{cases} \hphantom-a,&\text{если}~a\ge0,\\ -a,&\text{если}~a\lt0. \end{cases} $$

— Совершенно верно. Точно так же и в вашей задаче: нельзя писать $\sqrt{(x-3)^2}=(x-3)$‍,‍ потому что $(x-3)$‍‍ может быть и отрицательным числом. Если воспользоваться тем, что $\sqrt{(x-3)^2}=|x-3|$‍,‍ то придём к уравнению $$ |x-3|=x-1{,}5. $$ Далее следует рассмотреть два случая: 1) $x-3\ge0$‍;‍ 2) $x-3\lt0$‍.‍ Вы рассмотрели только первый случай, поэтому вывод о том, что задача не имеет решения, был сделан преждевременно. Во втором случае $|x-3|=-(x-3)$‍.‍ Тогда из уравнения $-(x-3)=x-1{,}5$‍‍ получаем $x=2{,}25$‍,‍ т. е. $AC=2{,}25~\text{см}$‍.‍

— Всё ясно, — сказал Абитуриент.

— В таком случае нашу беседу будем считать законченной. На прощание позволю себе дать вам следующий совет: $$ \underline{\text{Не забывайте, что}~\sqrt{a^2}=|a|!} $$

На этом мы расстанемся с Абитуриентом и Экзаменатором, но совет Экзаменатора примем к сведению. В частности, применим его при решении следующего примера.

Пример 1. Упростить выражение $$ \sqrt{\dfrac{a+x^2}x-2\sqrt a}+\sqrt{\dfrac{a+x^2}x+2\sqrt a},\quad \text{если}~x\gt\sqrt a. $$

Решение. Имеем $$ \begin{gather*} \sqrt{\dfrac{a+x^2-2x\sqrt a}x}+\sqrt{\dfrac{a+x^2+2x\sqrt a}x}=\\ =\dfrac{\sqrt{(\sqrt a-x)^2}}{\sqrt x}+\dfrac{\sqrt{(\sqrt a+x)^2}}{\sqrt x}= \dfrac{|\sqrt a-x|}{\sqrt x}+\dfrac{|\sqrt a+x|}{\sqrt x}. \end{gather*} $$ Так как по условию $x\gt\sqrt a\ge 0$‍,‍ то $|\sqrt a-x|=-\sqrt a+x$‍,‍ $|\sqrt a+x|=\sqrt a+x$‍,‍ и данное выражение преобразуется так: $$ \dfrac{-\sqrt a+x+\sqrt a+x}{\sqrt x}=2\sqrt x. $$

Несколько слов о свойствах радикалов

При решении примеров на действия с радикалами приходится применять различные свойства радикалов. Так, в примере 1 мы воспользовались, причём довольно-таки беззаботно, известным свойством: $\sqrt{\dfrac ab}=\dfrac{\sqrt a}{\sqrt b}$‍.‍ Однако следует учесть, что это равенство имеет место лишь в случае, когда $a\ge0$‍‍ и $b\gt0$‍.‍ Если же $a$‍‍ и $b$‍‍ — отрицательные числа, то запись $\dfrac{\sqrt a}{\sqrt b}$‍‍ не имеет смысла в области действительных чисел. В примере 1, нa наше счастье, ошибки не произошло, так как $(\sqrt a-x)^2\gt0$‍,‍ $(\sqrt a+x)^2\gt0$‍‍ и, кроме того, по условию $x\gt0$‍.‍ Ho, во всяком случае, из сказанного выше можно сделать следующий вывод: надо быть очень внимательным, раскрывая корень (чётной степени) из произведения или из дроби. В общем случае, когда знак $a$‍‍ и $b$‍‍ неизвестен, целесообразно проводить следующие рассуждения: $$ \sqrt{\dfrac ab}=\sqrt{\dfrac{|a|}{|b|}}=\sqrt{\dfrac{|a|}{|b|}}=\dfrac {\sqrt{|a|}}{\sqrt{|b|}}. $$

$\underline{\text{Итак, если числа}~a~\text{и}~b~\text{имеют одинаковые знаки, то}}$‍‍ $$ \underline{\sqrt{\dfrac ab}=\dfrac{\sqrt{|a|}}{\sqrt{|b|}}} $$ и аналогично $$ \underline{\sqrt{ab}=\sqrt{|a|}\cdot\sqrt{|b|}.} $$

Пример 2. Упростить $$ \sqrt{\dfrac{a-\sqrt x}{a+\sqrt x}}+ \sqrt{\dfrac{a+\sqrt x}{a-\sqrt x}}- \sqrt{\dfrac{16}{a^2-x}},\quad \text{если}~x=4(a-1). $$

Решение. Выразим, наоборот, $a$‍‍ через $x$‍:‍ $a=\dfrac{x+4}4$‍,‍ и подставим в данное выражение. Оно преобразуется так: $$ \begin{gather*} \sqrt{\dfrac{x-4\sqrt x+4}{x+4\sqrt x+4}}+ \sqrt{\dfrac{x+4\sqrt x+4}{x-4\sqrt x+4}}- \sqrt{\dfrac{16^2}{(x+4)^2-16x}}=\\ =\dfrac{|\sqrt x-2|}{|\sqrt x+2|}+ \dfrac{|\sqrt x+2|}{|\sqrt x-2|}- \dfrac{16}{\sqrt{x^2-8x+16}}=\\ =\dfrac{(x-4\sqrt x+4)+(x+4\sqrt x+4)}{|(\sqrt x)^2-4|}- \dfrac{16}{|x-4|}=\dfrac{2x+8}{|x-4|}-\dfrac{16}{|x-4|}=2\dfrac{x-4}{|x-4|}. \end{gather*} $$ Заметим ещё, что $x\gt4$‍,‍ если $a\gt2$‍,‍ и $x\lt4$‍,‍ если $1\le a\lt2$‍‍

Окончательный ответ: $$ \begin{cases} \hphantom{-}2,&\text{если}~a\gt2,\\ -2,&\text{если}~1\le a\lt2. \end{cases} $$

Мы пользовались — и это часто бывает полезно — такими свойствами модуля: для всех $a$‍‍ и $b$‍‍ $$ |a|\cdot|b|=|ab|,\quad|a|^2=a^2. $$ А сейчас мы остановимся ещё на одном важном свойстве корня.

Пример 3. Упростить $$ \sqrt[10]{\dfrac12(19+6\sqrt{10})}\cdot\sqrt[5]{3\sqrt2-2\sqrt5}. $$

Решение. Часто рассуждают так. Пользуясь известным свойством корня, можно у второго сомножителя показатель корня умножить на 2 и одновременно подкоренное выражение возвести в квадрат; получим $$ \begin{gather*} \sqrt[10]{\dfrac12(19+6\sqrt{10})}\cdot\sqrt[5]{3\sqrt2-2\sqrt5}=\\ =\sqrt[10]{\dfrac12(19+6\sqrt{10})}\cdot\sqrt[10]{(3\sqrt2-2\sqrt5)^2}=\\ =\sqrt[10]{\dfrac12(19+6\sqrt{10})(38-12\sqrt{10})}= \sqrt[10]{19^2-(6\sqrt{10})^2}=\sqrt[10]1=1. \end{gather*} $$ Но здесь есть ошибка! Правильный ответ — минус единица. Дело в том, что $3\sqrt2-2\sqrt5\lt0$‍,‍ поскольку $(3\sqrt2)^2=18\lt(2\sqrt5)^2=20$‍.‍ Поэтому неверно, что $$ \sqrt[5]{3\sqrt2-2\sqrt5}=\sqrt[10]{(3\sqrt2-2\sqrt5)^2}, $$ а верно, что $$ \sqrt[5]{3\sqrt2-2\sqrt5}=-\sqrt[5]{2\sqrt5-3\sqrt2}= -\sqrt[10]{(2\sqrt5-3\sqrt2)^2}. $$

Пример 4. Упростить $\sqrt[8]{(\pi^2-10)^4}$‍.‍

Здесь тоже неверно было бы просто разделить показатель корня и подкоренного выражения на 4: $$ \sqrt[8]{(\pi^2-10)^4}=\sqrt{\pi^2-10} $$ (полученный результат не имеет смысла, поскольку $\pi^2\lt10$‍).‍ Верное равенство такое: $$ \sqrt[8]{(\pi^2-10)^4}=\sqrt{10-\pi^2}. $$

---

В итоге мы приходим к такому выводу:

Пользуясь основными свойствами радикалов в тех случаях, когда нет уверенности, что под корнем стоит положительное число, нужно следить, чтобы, во-первых, полученный результат имел смысл (при необходимости нас выручит знак модуля) и, во-вторых, чтобы полученный результат имел тот же знак, что и первоначальное выражение.

Задачи

1. Перечислите условия, при которых верны следующие равенства ($k$‍‍ и $n$‍‍ — натуральные числа):

   1. $\sqrt[n]{-a}=-\sqrt[n]a$‍;‍
   2. $\sqrt[n]{a^n}=a$‍;‍
   3. $(\sqrt[n]a)^n=a$‍;‍
   4. $\sqrt[n]{a\cdot b}=\sqrt[n]a\cdot\sqrt[n]b$‍;‍
   5. $\sqrt[n]{\dfrac ab}=\dfrac{\sqrt[n]a}{\sqrt[n]b}$‍;‍
   6. $a\cdot\sqrt[n]b=\sqrt[n]{a^nb}$‍;‍
   8. $\sqrt[n]a=\sqrt[nk]{a^k}$‍;‍
   9. $\sqrt[k]{\sqrt[n]a}=\sqrt[nk]a$‍;‍
   10. $(\sqrt[n]a)^k=\sqrt[n]{a^k}$‍;‍
   12. если $a\lt b$‍,‍ то $\sqrt[n]a\lt\sqrt[n]b$‍.‍

2. Упростить следующие выражения:

   1. $\left(\sqrt{\dfrac{a+1}{a-1}}+\sqrt{\dfrac{a-1}{a+1}}\right): \left(\sqrt{\dfrac{a+1}{a-1}}-\sqrt{\dfrac{a-1}{a+1}}\right)$‍;‍
   2. $\sqrt{\dfrac{3y+x^2}{2x}+\sqrt{3xy}}-\sqrt{\dfrac{3y+x^2}{2x}-\sqrt{3xy}} $‍;‍
   3. $\dfrac{(4a^2m^{-2}+a^{-2}m^2-4)^{-\tfrac12}}{2ma(m^2-a^2)^{-\tfrac12}} \cdot\left(2\sqrt{m^4-\dfrac{a^2}{m^{-2}}}-\dfrac{2a^2}{\sqrt{1-a^2m^{-2}}} \right)$‍;‍
   4. $\dfrac{a+\sqrt{2+\sqrt5}\cdot\sqrt[12]{(9-4\sqrt5)^3}}{\sqrt[3]{2-\sqrt5} \cdot\sqrt[6]{9+4\sqrt5}-\sqrt[3]{a^2}+\sqrt[3]a}$‍.‍