Левантовский В. И.

Размышления по поводу притяжения Земли на полюсе и на экватореЛевантовский В. И. Размышления по поводу притяжения Земли на полюсе и на экваторе // Квант. — 1970. — № 3. — С. 28‍—‍32.‍‍

Хорошо известно, что вес тела‍ изменяется в зависимости от географической широты места. Одно и то же тело весит больше всего на полюсе и меньше всего на экваторе. В любом учебнике физики — и в школьном и в вузовском — можно прочесть, что это происходит по двум причинам.

Во-первых, вследствие вращения Земли тело, находящееся на экваторе, описывает окружность и поэтому давит на горизонтальную опору с силой, меньшей силы притяжения тела Землёй. Объясняется это просто. На тело действуют сила притяжения, направленная к центру Земли, и противоположная ей сила реакции опоры. Эти две силы сообщают телу центростремительное ускорение, равное $\omega^2R$‍,‍ где $\omega$‍‍ — угловая скорость, а $R$‍‍ — экваториальный радиус Земли. Если $m$‍‍ — масса тела, $F$‍‍ — сила притяжения, а $N$‍‍ — реакция опоры, то $F-N=m\omega^2R$‍.‍ Отсюда $N=F-m\omega^2R$‍,‍ т. е. реакция опоры $N$‍‍ меньше силы притяжения. А ведь эта реакция и равна по величине весу тела. Значит, вес тела на экваторе меньше силы притяжения тела Землёй. На полюсе же вес равен силе притяжения, так как никакой окружности там тело вокруг земной оси не описывает.

Во-вторых, говорят обычно, сама сила притяжения на полюсе больше, чем на экваторе, так как, находясь на полюсе, тело расположено ближе к центру Земли, чем когда оно находится на экваторе. А чем ближе к центру Земли, тем сила притяжения больше: ведь сила притяжения по закону всемирного тяготения Ньютона изменяется обратно пропорционально квадрату расстояния.

Автор должен извиниться перед читателями за то, что все эти хорошо знакомые доводы он привёл здесь столь подробно. Сделал он это потому, что со вторым доводом дело обстоит не так просто. У нас нет никаких логических оснований утверждать, что одно и то же тело на полюсе притягивается Землёй сильнее, чем на экваторе. Ссылка на закон всемирного тяготения несостоятельна. Этот закон утверждает, что две материальные точки притягивают друг друга с силами, обратно пропорциональными квадрату расстояния. Земля же не точка, а материальное тело, состоящее из многих частиц, каждая из которых притягивает другую частицу, расположенную вне или внутри Земли, по закону обратной пропорциональности квадрату расстояния.

Можно ли заменить притягивающее тело материальной точкой, сосредоточив всю массу тела в его центре тяжести (центре масс)? Отнюдь не всегда. Оказывается, однородное тело кубической формы притягивает совсем иначе, чем однородное тело той же массы, но сферическое или цилиндрическое, даже если центры тяжести (центры масс) этих тел занимают одно и то же место в пространстве. Один и тот же кусок глины у нас в руке притягивает по-разному в зависимости от той формы, которую мы ему придаём.

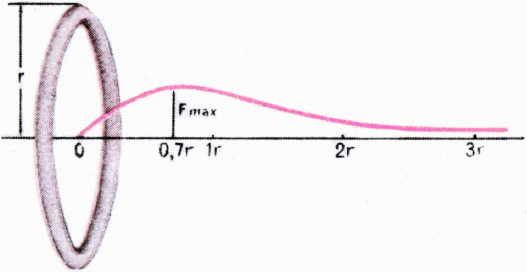
На первый взгляд это кажется неожиданным. Но давайте представим себе, как будет притягивать круглое бесконечно тонкое материальное кольцо какую-нибудь материальную точку, находящуюся на оси кольца, перпендикулярной к его плоскости. Если эта точка расположена очень далеко от кольца, то она, конечно, весьма слабо притягивается кольцом. По мере приближения точки к кольцу притяжение его сначала увеличивается, но с какого-то расстояния неизбежно должно уменьшаться, так как в центре кольца силы притяжения от противоположных частиц уравновешиваются и, значит, кольщо в целом вовсе не притягивает материальную точку, когда она находится в его центре. Как показывает математический расчёт, максимальным притяжение будет в точке, находящейся на расстоянии $\approx0{,}7r$‍‍ от центра кольца. На рисунке 1 показан график изменения силы притяжения кольца в зависимости от расстояния притягиваемой точки от центра. Этот график изображает такой закон притяжения, который, по крайней мере вблизи кольца, ничуть не напоминает закон обратной пропорциональности квадрату расстояния. Значит, массу кольца нельзя «сосредоточить в его центре тяжести».

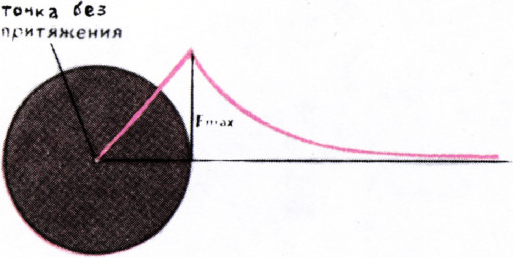
Существует ли форма тела, псзволяющая мысленно сосредоточить его массу в центре тяжести и быть уверенным, что после такой операции поле тяготения тела останется прежним? Да, существует. Однородный шар притягивает любую материальную точку так, как будто бы вся его масса сосредоточена в центре. Правда, это касается только точек, расположенных вне шара. Точки же, расположенные внутри шара, притягиваются совершенно иначе. В центре притяжение шара, очевидно, равно нулю, у поверхности оно максимально, а между центром и поверхностью изменяется, как показывает математический расчёт, по закону прямой пропорциональности: чем дальше от центра, тем притяжение больше. (График изменения силы притяжения однородного шара в зависимости от расстояния до центра показан на рисунке 2.)

Ещё более любопытен случай притяжения шара со сферическим вырезом в середине. В известном научно-фантастическом романе В. А. Обручева «Плутония» повествуется о путешествии в недра Земли, причём наша планета оказывается полой. В центре полости путешественники обнаружили раскалённое тело. В отличие от автора романа допустим, что в центре Земли никакого тела нет и что Земля представляет собой однородный шар с пустой шарообразной же сердцевиной. Можно доказать, что, каков бы ни был радиус «выреза», внутри полости в любой её точке (а не только в центре!) притяжение полностью отсутствует. Это, в частности, говорит о том, что в ней должна господствовать невесомость, которая, однако, объясняется иной причиной, чем невесомость при космических полётах.

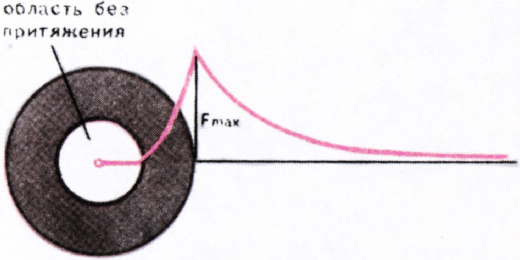
На рисунке 3 показан график изменения силы притяжения гипотетической пустотелой Земли в зависимости от расстояния до центра. Внутри массивного сферического слоя притяжение возрастает по мере удаления от центра и достигает максимума на поверхности. Вне поверхности поле тяготения такое же, как у материальной точки, находящейся в центре этого пустотелого шара.

Земля по форме довольно близка к шару. Но наша планета не однородна: плотность составляющих её пород в различных точках различна. Наибольшей плотностью обладает ядро Земли. Правдоподобно предположить, что плотность земных пород на одинаковых расстояниях от центра Земли одинакова. Иными словами, Землю можно в первом приближении представить себе состоящей из вложенных друг в друга однородных сферических слоёв. О таком теле говорят, что распределение плотности в нём обладает сферической симметрией. Можно доказать, что такой шар, как и однородный, притягивает любую частицу вне его поверхности или на ней так, как будто бы вся его масса сосредоточена в центре.

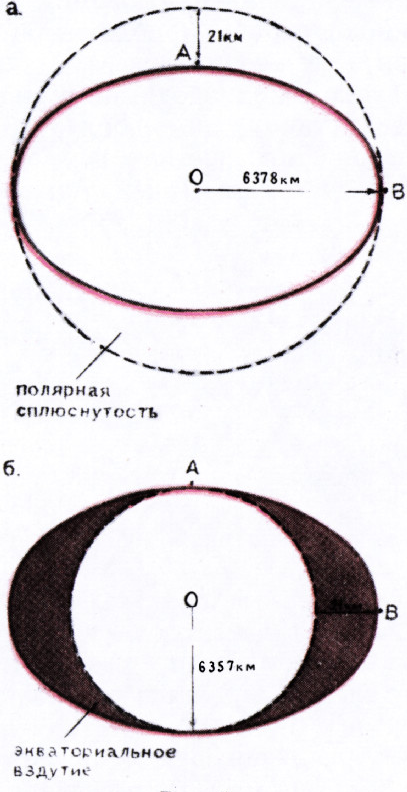
Но реальная Земля является не шаром, а так называемым сфероидом. Нашу планету можно рассматривать как приплюснутый у полюсов шар с радиусом, равным экваториальному радиусу Земли (рис. 4, а). Величина приплюснутости равна 21 км. С другой стороны, тот же сфероид можно представить себе как шар с радиусом, равным полярному радиусу Земли (6357 км), к которому добавлена масса с боков — так называемое «экваториальное вздутие» (рис. 4, б). Толщина вздутия на экваторе составляет 21 км. Притяжение сфероидом любой материальной частицы можно рассматривать как состоящее из двух частей: из притяжения центрального шара радиуса 6357 км, изображённого на рис. 4, б, и из притяжения экваториального вздутия. Наличие вздутия приходится учитывать во многих случаях, например при расчёте траекторий космических кораблей и даже орбиты Луны.

Рассмотрим теперь два одинаковых тела, лежащих на поверхности Земли: тело $A$‍‍ находится на полюсе, тело $B$‍‍ — на экваторе. Шар радиуса 6357 км притягивает тело $A$‍,‍ конечно, сильнее, чем тело $B$‍,‍ так как тело $B$‍‍ расположено на 21 км дальше от центра Земли. Но, кроме того, на оба тела ещё действует притяжение экваториального вздутия. Не производя точного математического расчёта, невозможно сказать, каков будет окончательный итог и какое из притяжений сфероида в целом окажется больше: в точке $A$‍‍ или в точке $B$‍.‍ Анализ, производимый средствами высшей математики, показывают, что притяжение сфероидом тела на полюсе больше, чем притяжение им тела на экваторе, но, как видим, дело обстоит отнюдь не так просто, как это обычно утверждается.