Н. В.

Размышления по дороге в школу. 2. В автобусеН. В. Размышления по дороге в школу. 2. В автобусе // Квант. — 1970. — № 2. — С. 59.‍‍

2. В автобусе

В автобус, идущий без кондуктора, вошло 15 незнакомых между собой человек. Ни у кого из них нет медных денег, а есть только монеты достоинством в 10, 15 и 20 копеек. (Билет стоит 5 копеек. В кассу можно бросить любую монету и оторвать соответствующее количество билетов.) Тем не менее вошедшие пассажиры смогли расплатиться за проезд, взяв сдачу друг у друга. Подумайте, как это могло быть?

Тем, кто решил эту задачу, предлагаем решить три более трудные:

1. Докажите, что у этих пассажиров было не меньше 20 серебряных монет (иначе они не смогли бы расплатиться!).
2. Докажите, что у них было не меньше восьми 15-копеечных монет.
3. 3. Докажите, что у всех пассажиров вместе было не меньше 2 р. 50 к.

Конечно, придумать пример, когда $N$‍‍ пассажиров расплачиваются только монетами достоинством в 10, 15, 20 копеек, можно для любого $N\geq2$‍.‍ Подумайте, каковы точные оценки для общего количества монет, общего количества 15-копеечных монет и общего количества денег в этом случае?

---

Ответы

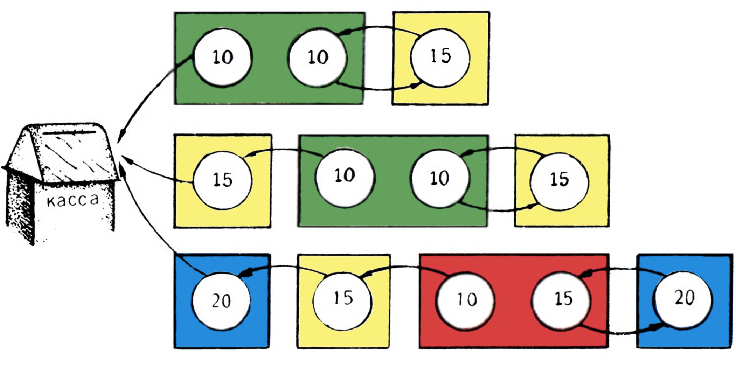
Легко сообразить, как могут рассчитаться двое, трое или четверо пассажиров (некоторые варианты изображены на рис. 1) и, пользуясь этим, построить много разных примеров, как могли рассчитаться 15 пассажиров.

1. Заметьте, что при каждом способе расчёта не менее 5 монет опущено в кассу и не менее 15 осталось у пассажиров. Нетрудно построить пример, когда общее число монет у всех пассажиров — 20.
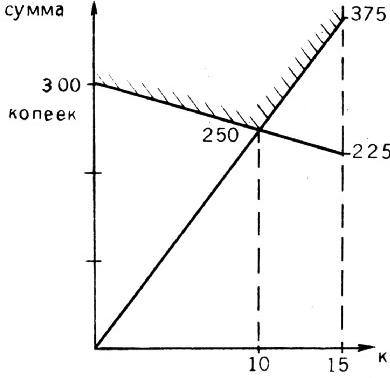
3. Докажите, что если среди 15 человек $k$‍‍ таких, у которых есть только одна монета в 15 коп., то общее количество денег, во-первых, не меньше $15k+20(15-k)$‍‍ копеек и, во-вторых, не меньше $15k+20k$‍‍ копеек (рис. 2). Постройте пример, когда общая сумма — 2 р. 50 к.!

В общем случае — для $N$‍‍ пассажиров — ответы такие:

1. минимально возможное количество монет у всех пассажиров (при котором они ещё могут рассчитаться) $\left[\dfrac{5N+3}4\right]$‍;‍
2. минимально возможное общее количество 15-копеечных монет $\left[\dfrac{N+1}2\right]$‍;‍
3. минимально возможная общая сумма денег $15N+5\left[\dfrac{N+2}3\right]~\text{коп.}$‍;‍

здесь через $[x]$‍‍ мы обозначаем целую часть числа $x$‍,‍ т. е. наибольшее целое число, не превосходящее $x$‍.‍ (Без этого обозначения ответы можно сформулировать так: 1) $N$‍‍ монет и ещё по одной монете на каждую полную или неполную четвёрку пассажиров; 3) 15 коп. у каждого и ещё по 5 коп. на каждую полную или неполную тройку пассажиров.)