Колмогоров А. Н.

Что такое график функцииКолмогоров А. Н. Что такое график функции // Квант. — 1970. — № 2. — С. 3‍—‍13.‍‍

Здесь продолжается изложение новой, более общей точки зрения на хорошо известные из школы понятия — функция и её график. Начало этого изложения было в статье «Что такое функция», помещённой в первом номере «Кванта». Для понимания настоящей статьи необходимо владеть понятиями, которые определены в первой статье.

1. Напоминание и небольшие дополнения

В первом номере журнала по статье «Что такое функция» вы познакомились с современным общим пониманием слова функция: функция — это совершенно произвольное отображение некоторого множества $E$‍‍ на другое множество $M$‍.‍ Множество $E$‍‍ называется областью определения функции, а множество $M$‍‍ — множеством её значений. Чтобы задать функцию с областью определения $E$‍,‍ надо указать для каждого элемента $x$‍‍ этого множества вполне определённый объект‍$$ y=f(x). $$ Каким бы способом мы это ни сделали, мы получим функцию с областью определения $E$‍.‍ Если множество $E$‍‍ состоит из учеников вашего класса, то можно, например, для любого ученика $x$‍‍ принять за $y=f(x)$‍‍ вторую букву его имени (предполагая, что в классе нет учеников, имя которых состоит из одной-единственной буквы, — хотя я и знал девочку Олю, которую звали просто «О»).

При таком задании функции само собой определится множество её значений $M$‍;‍ это множество всех тех объектов $y$‍,‍ для которых существует хоть один элемент $x$‍‍ множества $E$‍,‍ для которого $$ f(x)=y. $$ Поэтому, описывая смысл термина функция, можно и не говорить в описании явно о множестве значений. Правильно будет, например, просто сказать, что «функция есть закон, по которому каждому элементу $x$‍‍ некоторого множества $E$‍‍ поставлен в соответствие вполне определённый объект $y=f(x)$‍‍». Мы подчёркивали, впрочем, что все эти описания лучше не считать определениями. Если бы мы захотели в самом деле определить понятие функции через понятие «закона», то с нас потребовали бы точное определение смысла термина «закон» и т. д. Понятие функции будем считать одним из основных понятий математики, смысл которого только поясняется, а не даётся формальным определением.

В школе вы привыкли иметь дело только с числовыми функциями, область определения которых состоит из чисел и значения которых являются числами. Смысл выражения «числовая функция числового аргумента» не вполне определён. Ведь само понятие числа в школе постепенно обобщается. Мы остановимся на системе всех действительных чисел, с которой школьники знакомятся в девятом классе. Действительные функции действительного аргумента и изучаются по преимуществу в старших классах средней школы. Их графики вы умеете вычерчивать на «числовой плоскости».

В школьных учебниках пишут, что «числовая плоскость» — это такая плоскость, на которой некоторым определённым образом введены координаты. Если верить учебникам буквально, то числовых плоскостей очень много. Проводя на классной доске оси координат, учитель превращает в «числовую плоскость» плоскость этой доски; ученики на страницах своих тетрадок изготовляют всё новые и новые «числовые плоскости», иногда по нескольку на одной странице!

В п. 3 этой статьи вы узнаете, с какой числовой плоскостью в действительности имеют дело математики. Но сначала мне хочется сделать одно дополнительное замечание к изложению статьи «Что такое функция».

В школьном курсе алгебры чаще всего имеют дело с функциями, заданными «аналитически» при помощи формулы. Областью определения такой функции, если не сказано ничего другого, считается множество всех тех значений аргумента, для которых все предписанные формулой операции над числами выполнимы. Будем, например, как это принято в школе, считать знак $\sqrt{~}$‍‍ знаком «арифметического» квадратного корня. Ясно, что формула $$ y=f(x)=(\sqrt x)^2\tag1 $$ позволяет вычислить по заданному $x$‍‍ соответствующее ему значение $y$‍‍ лишь при неотрицательном $x$‍‍ (иначе квадратный корень «не извлекается»).

При неотрицательном $x$‍‍ $$ y=f(x)=x.\tag2 $$ Формула (2) проще, чем формула (1), и хотелось бы её считать формулой, определяющей нашу функцию. Но область определения функции, заданной формулой (2), состоит не из одних неотрицательных числел $x$‍,‍ а из всех чисел $x$‍.‍ Если мы хотим дать новое определение той самой функции, которая определена формулой (1), надо написать $$ y=f(x)=\begin{cases}x&\text{при}~x\ge0,\\ \text{не определена}&\text{при}~x\lt0.\end{cases}\tag3 $$

Подобным же образом функцию $g(x)=\dfrac{x^3-1}{x-1}$‍‍ можно записать так: $$ g(x)=\begin{cases}x^2+x+1&\text{при}~x\ne1,\\ \text{не определена}&\text{при}~x=1.\end{cases}\tag4 $$

На школьных и вузовских экзаменах требуют полной точности в подобных вопросах.

2. График функции

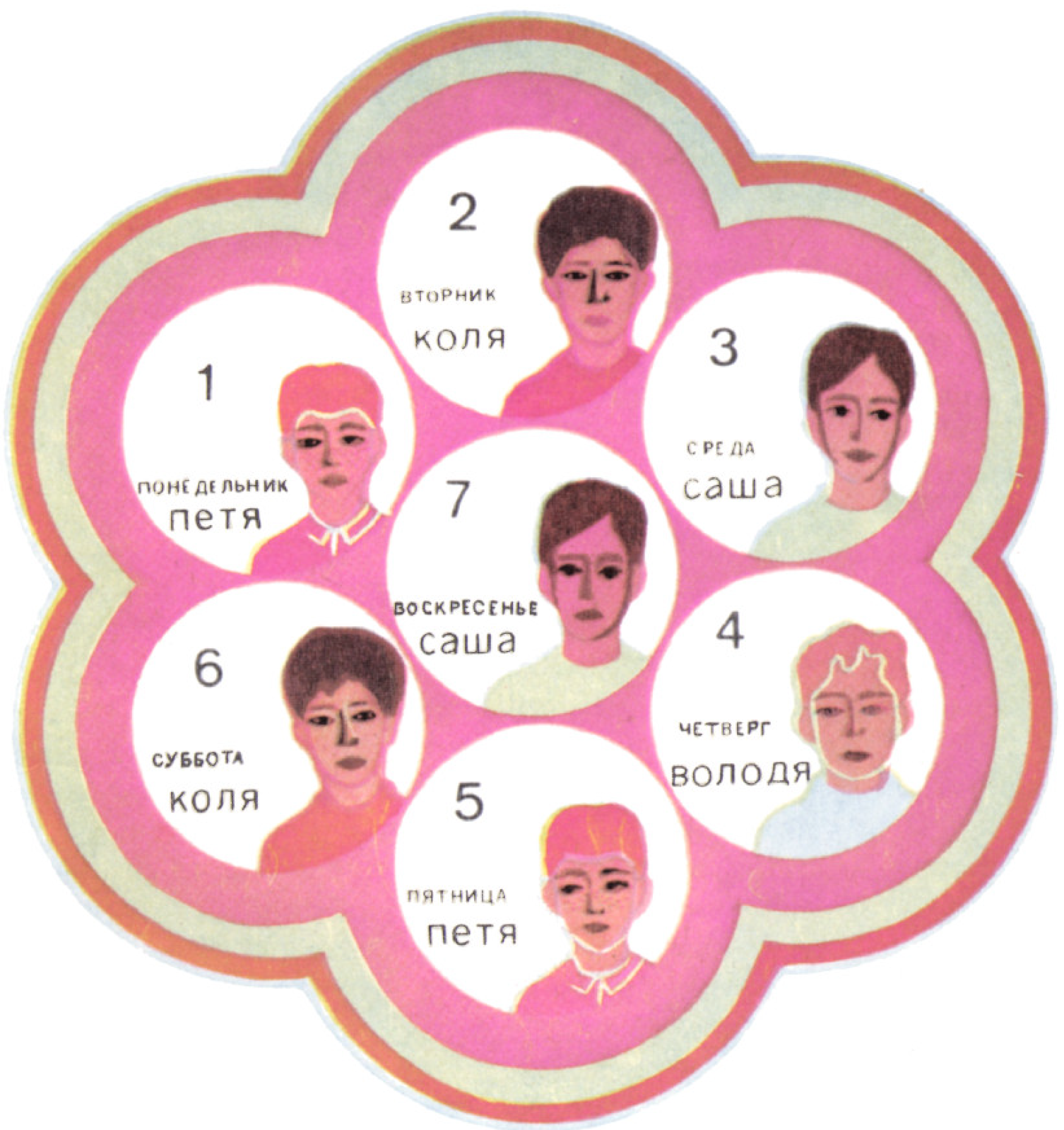
Рассмотрим следующий график дежурств (см. № 1 «Кванта», стр. 29):

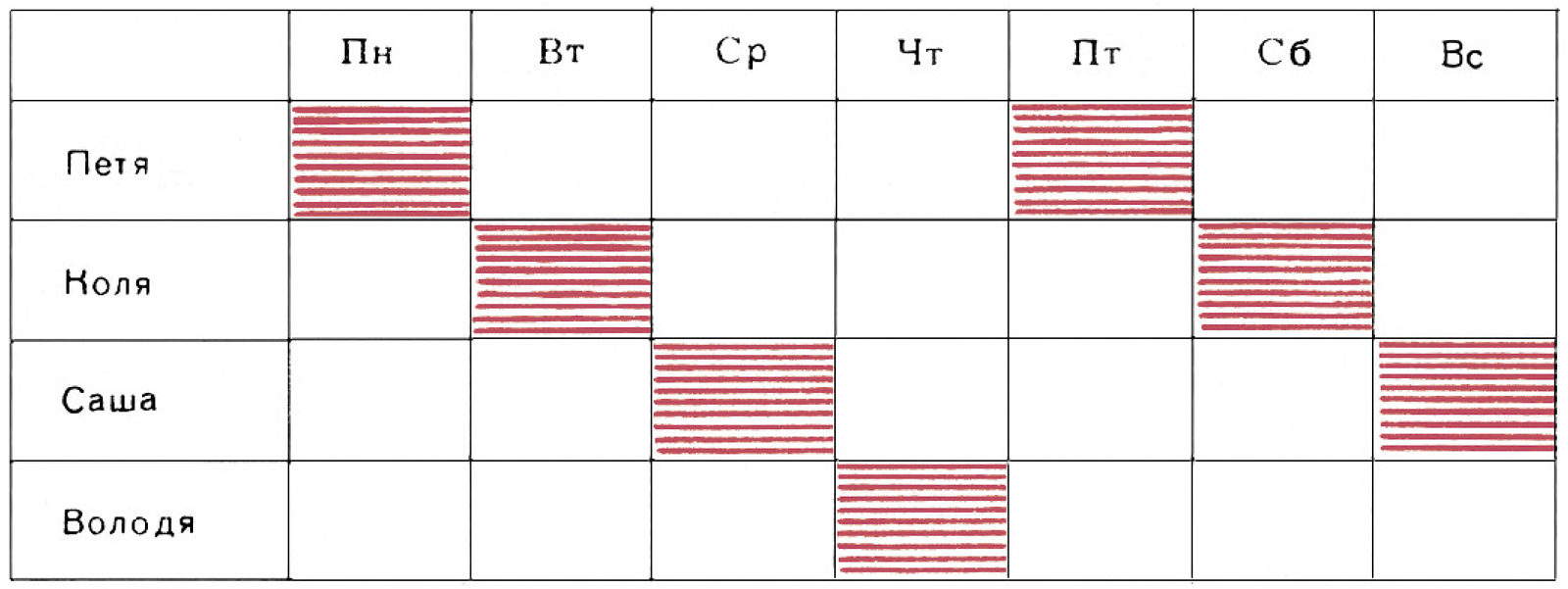
Мы уже знаем, что это график функции: имя дежурного можно считать функцией дня недели. Так как дней недели семь, а мальчиков четыре, то мы нарисовали $7\cdot4=28$‍‍ клеточек, но закрасили красным только семь из этих клеточек. Если бы мальчики решили расположить свои имена по алфавиту, то получилась бы табличка

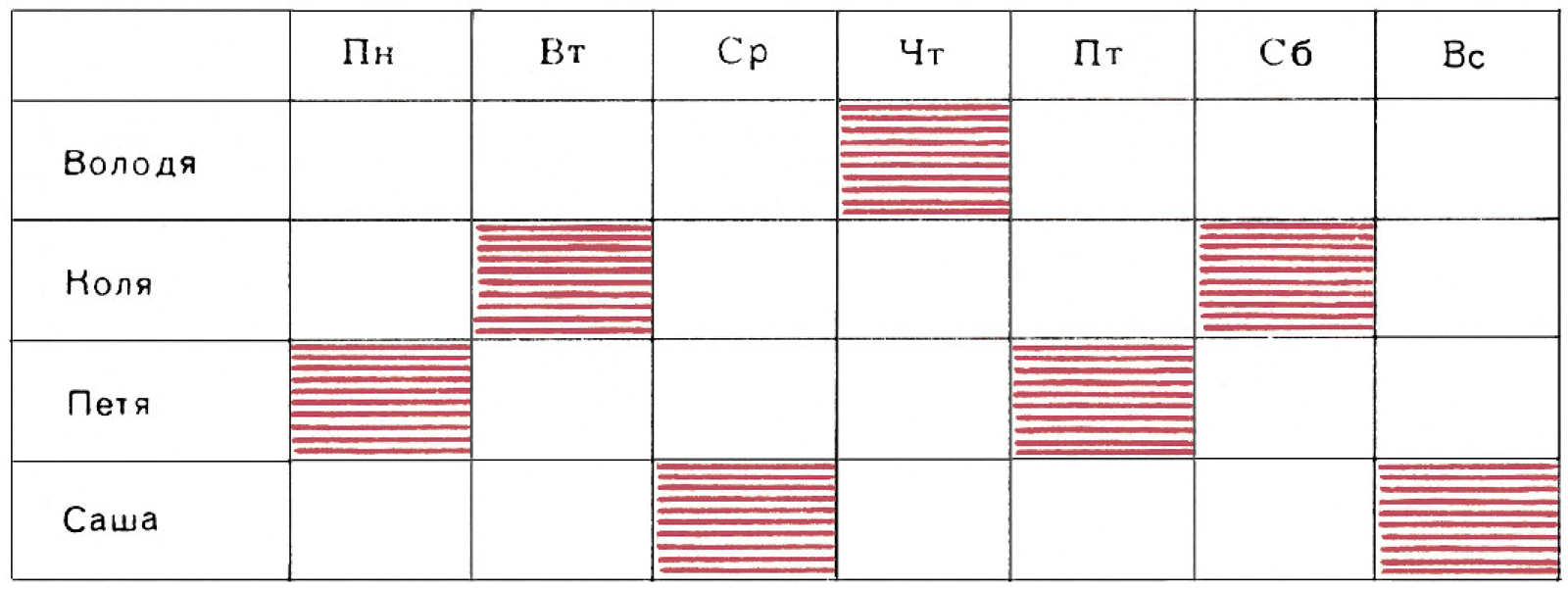
Выглядит она по-другому, но изображает то же самое распределение дежурств — ту же самую функцию.

В обеих табличках 28 клеточек соответствуют 28 возможным парам $$ (\text{день недели}, \text{мальчик}). $$ Из этих 28 пар выделены семь пар $$ \begin{gather*} (\text{пн},\text{Петя}),\quad(\text{вт},\text{Коля}),\quad (\text{ср},\text{Саша}),\quad(\text{чт},\text{Володя}),\\ (\text{пт},\text{Петя}),\quad(\text{сб},\text{Коля}),\quad (\text{вс},\text{Саша}), \end{gather*} $$ т. е. все пары, в которых день недели соединён с дежурным на этот день: $$ (\text{день недели}, \text{дежурный на этот день}), $$ или абстрактно: пары вида $$ (x,f(x)). $$ Только выбор этих пар и существен для задания функции.

После этого примера вам, быть может, не покажется неожиданным такое определение:

Графиком функции $f$‍‍ называется множество всех таких пар‍$$ (x,y), $$ что: 1) первый элемент пары $x$‍‍ принадлежит области определения функции, 2) второй элемент пары $$ y=f(x). $$

В нашем примере график функции $f$‍:‍ $$ \Gamma_f=\{(\text{пн},\text{Петя}),(\text{вт},\text{Коля}), (\text{ср},\text{Саша}),(\text{чт},\text{Володя}),(\text{пт},\text{Петя}), (\text{сб},\text{Коля}),(\text{вс},\text{Саша})\}. $$

Для функций, заданных таблицей $$ \colsep{2pt}{\begin{array}{c||c|c|c|c} &&&&\\[-6pt] x&f_1&f_2&f_3&f_4\\[-6pt] \qquad&\qquad&\qquad&\qquad&\qquad\\ \hline \hline &&&&\\[-6pt] A&A&B&A&B\\[-6pt] &&&&\\ \hline &&&&\\[-6pt] B&A&B&B&A\\[-6pt] &&&& \end{array}} $$ в соответствии с данным определением получим графики $$ \begin{gather*} \Gamma_1=\{(A,A),(B,A)\},\quad \Gamma_2=\{(A,B),(B,B)\},\\ \Gamma_3=\{(A,A),(B,B)\},\quad \Gamma_4=\{(A,B),(B,A)\}. \end{gather*} $$

Ясно, что для функций с конечной областью определения число элементов графика (т. е. число входящих в график пар) равно числу элементов области определения функции. Для функций с бесконечной областью определения все пары $(x,f(x))$‍‍ выписать нельзя. Приходится описывать эти пары при помощи их свойств.

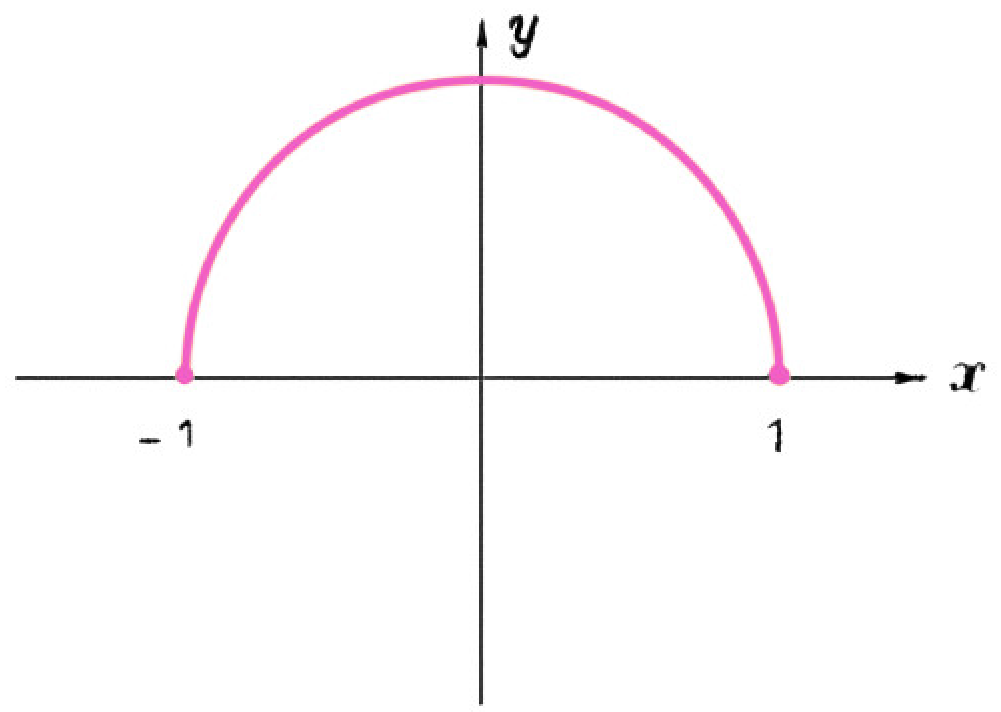
Например, для функции $$ y=f(x)=\sqrt{1-x^2} $$ график состоит из всевозможных пар чисел вида $$ (x,\sqrt{1-x^2}) $$ т. е. из всех пар $(x,y)$‍,‍ для которых выполнены два условия $$ x^2+y^2=1\quad\text{и}\quad y\ge0. $$ Это определение графика функции можно записать в виде $$ \Gamma_f=\{(x,y)\mid x^2+y^2=1{,}~y\ge0\}. $$

Само общее определение графика функции $f$‍‍ можно записать в виде такой формулы‍: $$ \Gamma_f=\{(x,y)\mid y=f(x)\}. $$

Определив график функции как множество пар, каждая из которых состоит из значения аргумента и значения функции, соответствующего этому значению аргумента, мы освободили понятие графика от всего случайного. В этом абстрактном понимании у каждой функции имеется один-единственный график.

3. Числовая плоскость

Обратимся к наиболее обычным в школе действительным функциям действительного переменного. В школе вы привыкли к тому, что графиком такой функции $f$‍‍ называется множество тех точек $P(x,y)$‍‍ числовой плоскости, координаты которых $x$‍‍ и $y$‍‍ удовлетворяют равенству $$ y=f(x). $$

Эта формулировка и общее определение графика, данное выше, в п. 2, похожи, но слегка отличаются. В п. 2 говорится о множестве пар $(x,y)$‍,‍ а в обычном школьном определении — о множестве точек $P$‍‍ с координатами $x$‍‍ и $y$‍.‍ Но нет ли возможности привести эти две формулировки к полному согласию?

Оказывается, это очень просто. Это простое решение и получило всеобщее распространение в современной научной литературе. По определению считают, что числовая плоскость есть множество всех пар действительных чисел. Числовую плоскость обозначают $\mathbb{R}^2$‍.‍ Её определение можно символически записать $$ \mathbb{R}^2=\{(x,y)\mid x\in\mathbb{R}{,}~y\in\mathbb{R}\}. $$ Немного подумав, вы сами убедитесь в том, что при таком определении числовой плоскости обычное школьное определение графика действительной функции действительного переменного становится частным случаем общего определения, данного в п. 2.

Обозначение $P(x,y)$‍‍ для точки с координатами $x$‍‍ и $y$‍‍ делается теперь излишним. Точками числовой плоскости в новом понимании являются просто сами пары чисел $(x,y)$‍.‍ Можно говорить просто о «точке $(0,0)$‍‍» (начало координат), о точках $(1,2)$‍,‍ $(-2,-1)$‍‍ и т. д.

Не лишне заметить, что и термину «числовая прямая» надо теперь придать новый смысл: числовая прямая — это просто само множество действительных чисел $\mathbb{R}$‍.‍ Естественно, что точками числовой прямой при этом надо считать просто сами действительные числа. Обычно в школьных учебниках этого не говорят прямо, но часто употребляют в применении к числам геометрический язык: множество чисел $$ [a,b]=\{x\mid a\le x\le b\} $$ называют «отрезком», говорят, что «точка» 2 принадлежит «отрезку» $[1,3]$‍‍ и т. п.

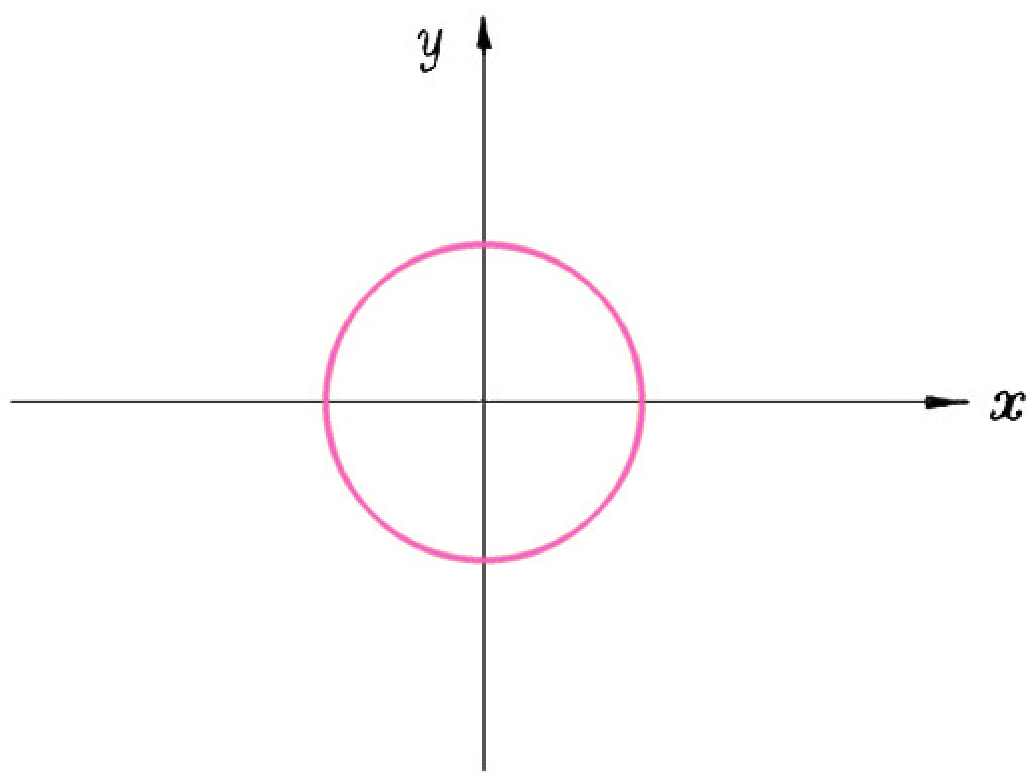
Любое множество точек числовой плоскости будем называть расположенной на числовой плоскости геометрической фигурой. Такова, например, окружность с центром $(0,0)$‍‍ и радиусом единица: это множество точек, т. е. пар чисел (х, у), для которых $$ x^2+y^2=1. $$ Естественно, что точки и геометрические фигуры числовой плоскости можно наглядно изображать на чертеже. Для этого на реальной плоскости (листе бумаги или классной доске) выбирают оси координат и точку числовой плоскости $(x,y)$‍‍ изображают реальной точкой с координатами $x$‍‍ и $y$‍.‍ Конечно, такое изображение может быть только приближённым. Начерченные на бумаге или классной доске графики являются лишь приближёнными изображениями «настоящих» графиков функций, которые в нашем новом понимании суть просто подмножества числовой плоскости. К этим «настоящим» графикам и относится утверждение, что функция полностью определяется своим графиком.

Пусть задано множество пар $$ M=\{(x,y)\}. $$ Таким множеством, например, является любая «фигура» на числовой плоскости. Что надо дополнительно потребовать, чтобы это множество пар было графиком некоторой функции?

Ответ не сложен: для этого необходимо и достаточно, чтобы в множестве $M$‍‍ нельзя было найти две пары $(x_1,y_1)$‍‍ и $(x_2,y_2)$‍‍ с общим первым элементом $x$‍‍ и различными вторыми элементами $y_1\ne y_2$‍.‍ (Проведите доказательство сами.) На рис. 1 красная кривая есть график функции, а чёрная графиком не является.

Множество пар $(x,y)$‍,‍ в котором не существует двух пар вида $(x,y_1)$‍,‍ $(x,y_2$‍),‍ $y_1\ne y_2$‍,‍ можно назвать функциональным графиком. Заметьте, что мы сейчас определили «функциональный график», не пользуясь понятием «функции». Нельзя ли с этой стороны дать формальное определение и самого понятия функции, которое мы считали основным, т. е. не подлежащим формальному определению? Я не хочу давать ответ на этот вопрос здесь. Он не совсем прост. В нашем журнале мы ещё будем иметь повод вернуться как к современным представлениям о понятии функции, так и к его истории.

4. Геометрические преобразования

Чтобы освоиться с широтой общего понимания термина «функция», рассмотрим ещё некоторые простейшие геометрические преoбразования.

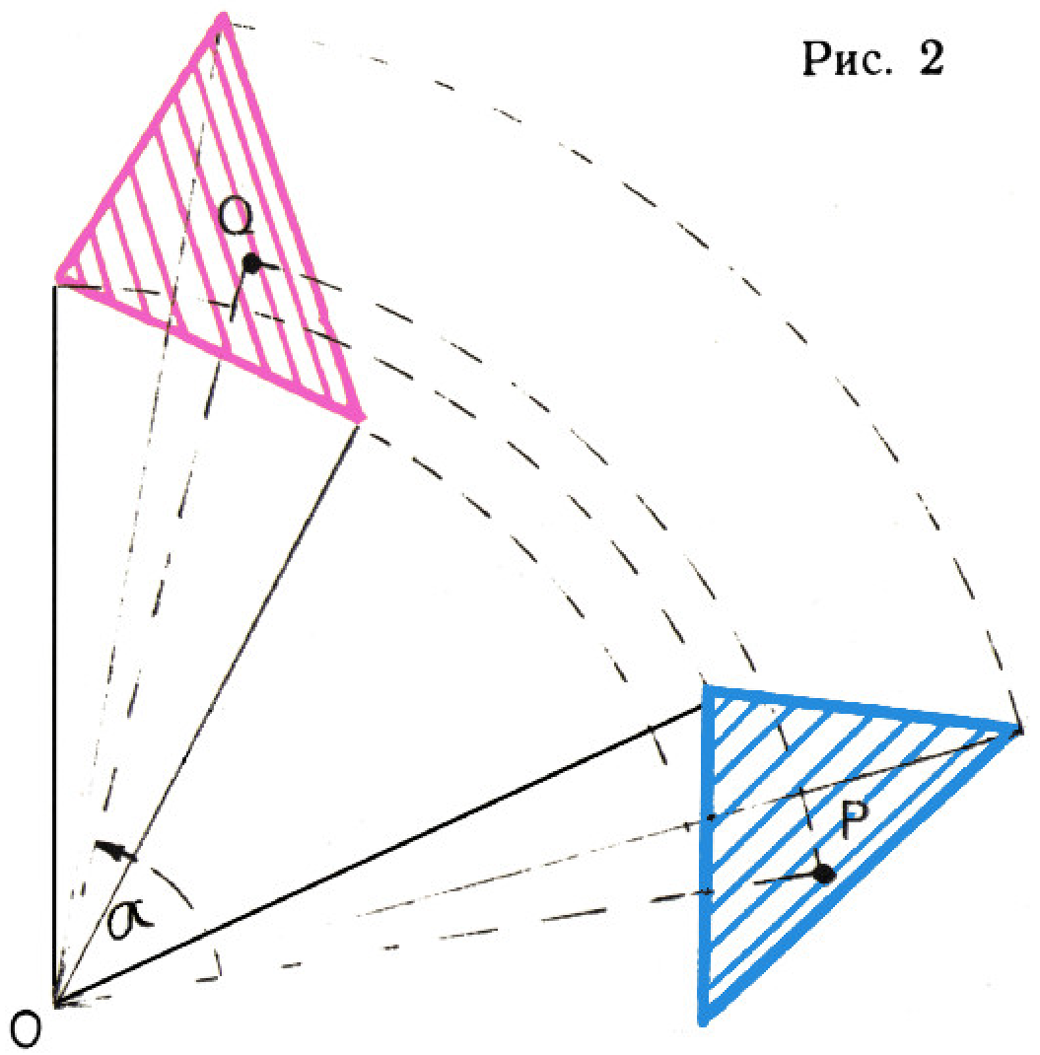
Чтобы повернуть плоскую фигуру вокруг точки $O$‍‍ (рис. 2), можно перенести контуры фигуры на наложенную на плоскость чертежа кальку, закрепить кальку булавкой в точке $O$‍‍ и, повернув кальку, перенести контуры копии фигуры с кальки на плоскость чертежа (например, при помощи копировальной бумаги). При повороте все точки фигуры поворачиваются вокруг точки $O$‍‍ в одном и том же направлении на один и тот же угол.

Обозначим $$ Q=\mathrm{R}_O^\alpha(P)\tag1 $$ положение точки $P$‍‍ после поворота на угол $\alpha$‍‍ против часовой стрелки. Если точка $O$‍‍ и угол $\alpha$‍‍ заданы, то каждой точке $P$‍‍ по формуле (1) соответствует вполне определённая точка $Q$‍.‍ Ясно, что в смысле нашего общего определения $\mathrm{R}_O^\alpha$‍‍ есть функция. Её областью определения является множество всех точек плоскости $P$‍.‍

Углы поворота указывают со знаком. На рис. 3 точка $Q_2$‍‍ получается из точки $P$‍‍ поворотом на $120^\circ$‍,‍ а точка $Q_1$‍‍ — поворотом на $-120^\circ$‍‍ (или поворотом на $240^\circ$‍).‍ Если точка $Q$‍‍ получена из точки $P$‍‍ поворотом на $\alpha$‍‍ градусов, то точку $P$‍‍ можно получить, повернув $Q$‍‍ на $-\alpha$‍‍ градусов: если $$ Q=\mathrm{R}_O^\alpha(P), $$ то $$ P=\mathrm{R}_O^{-\alpha}(Q). $$ Мы видим, что поворот $\mathrm{R}_O^\alpha$‍‍ всегда является обратимой функцией.

В применении к поворотам чаще говорят об «отображениях». Отображение, обратное к повороту $\mathrm{R}_O^\alpha$‍,‍ есть поворот $\mathrm{R}_O^{-\alpha}$‍.‍ Символически можно написать: $$ \begin{gather*} \mathrm{R}_O^{-\alpha}(\mathrm{R}_O^\alpha(P))=P,\\ (\mathrm{R}_O^\alpha)^{-1}=\mathrm{R}_O^{-\alpha}. \end{gather*} $$

Поворот отображает множество точек плоскости на самого себя. Если считать, что плоскость есть не что иное, как множество своих точек (так и поступают в современном изложении геометрии), то можно сказать, что поворот есть обратимое отображение плоскости на себя.

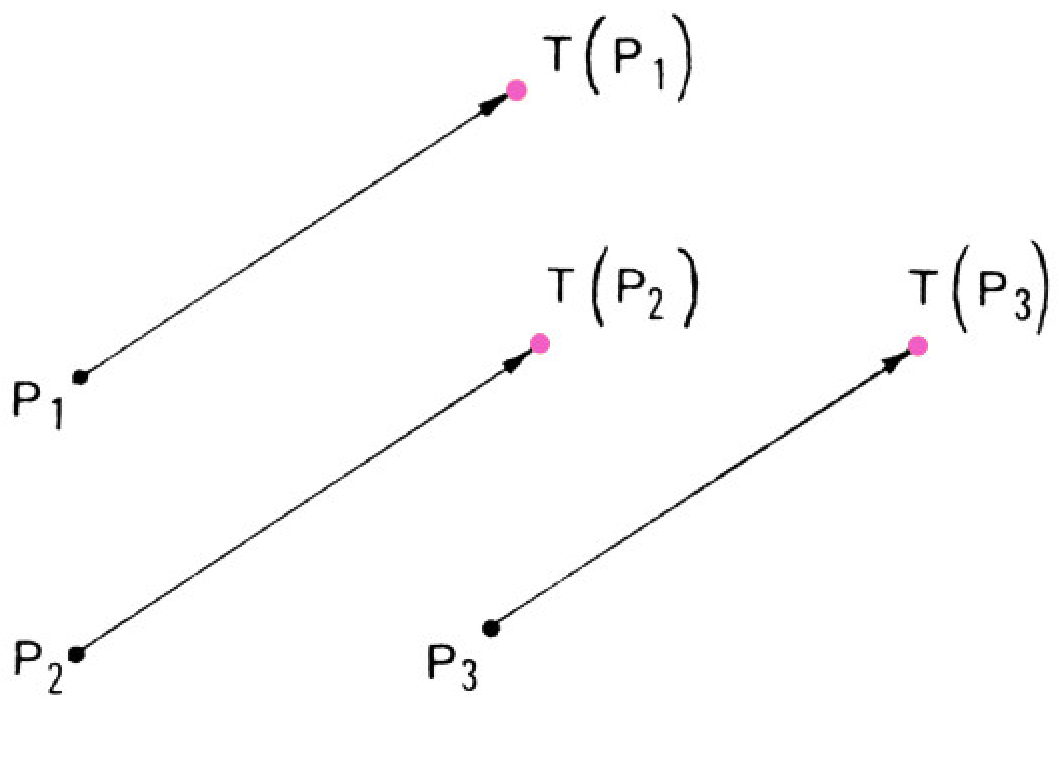
Обратимые отображения плоскости на себя и называются геометрическими преобразованиями плоскости. С геометрическими преобразованиями вы ещё неоднократно встретитесь на страницах нашего журнала. Пока же приведём ещё только один пример геометрического преобразования плоскости. Параллельным переносом называется отображение плоскости на себя $$ P\to Q=\mathrm{T}(P), $$ при котором все точки $P$‍‍ перемещаются на одно и то же расстояние и в одном и том же направлении (рис. 4).

5. Векторы

Хотя возможно, что вы уже устали от знакомства с новыми понятиями и необычным толкованием понятий вам уже известных, сделаем ещё одно усилие. Постараемся понять, что такое график параллельного переноса $P\to Q=\mathrm{T}(P)$‍.‍ По общему определению это — множество всех таких пар точек $$ (A,B), $$ для которых $$ B=\mathrm{T}(A). $$ Выберем одну такую пару точек $(A_0,B_0)$‍.‍ Чем характеризуются остальные? Тем, что отрезки $AB$‍‍ равны по длине и одинаково направлены с отрезком $A_0B_0$‍‍ (рис. 5). График параллельного переноса $\mathrm{T}$‍‍ есть по определению множество всех таких пар точек $(A,B)$‍.‍

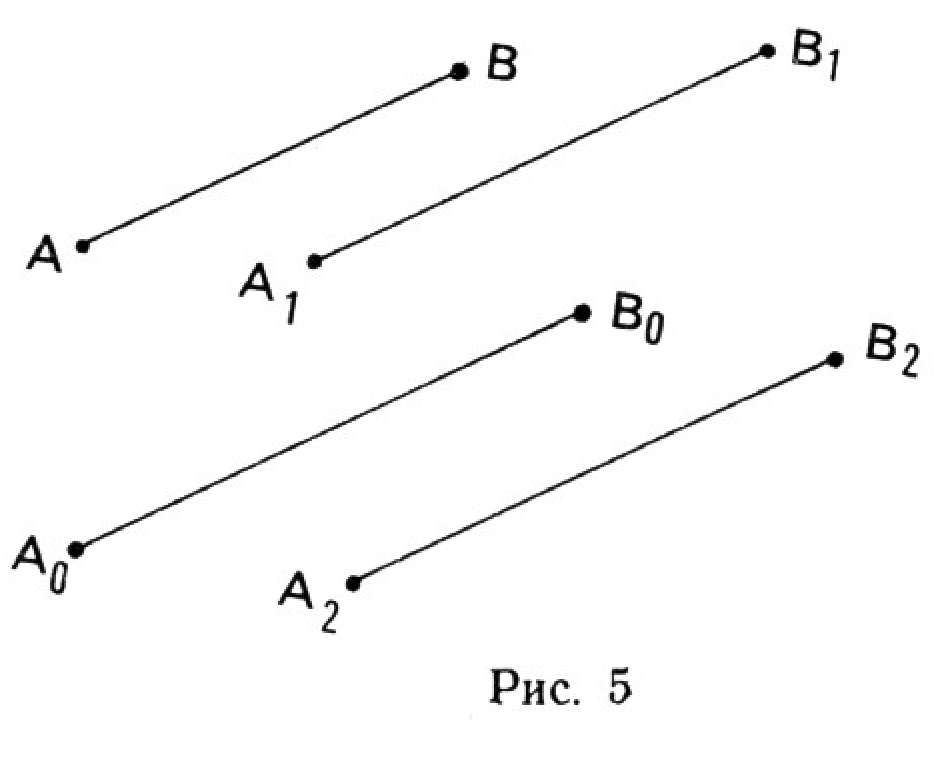
Обычно считают, что любая пара точек $(A,B)$‍‍ определяет «связанный «вектор» $\overrightarrow{AB}$‍,‍ связанные же векторы $\overrightarrow{AB}$‍‍ и $\overrightarrow{A'B'}$‍‍ определяют один и тот же свободный вектор», если отрезки $AB$‍‍ и $A'B'$‍‍ равны по длине и имеют общее направление.

Проще сказать, что «связанный вектор» — это просто сама пара точек $(A,B)$‍,‍ а «свободный вектор» $\overrightarrow{AB}$‍‍ — это множество всех связанных векторов $(A',B')$‍,‍ равных $(A,B)$‍‍ по длине и направлению. А при общем определении графика это множество есть не что иное, как график параллельного переноса $\mathrm{T}$‍,‍ который определяется тем, что $$ \mathrm{T}(A)=B. $$

Если $$ \mathrm{T}(A_1)=B_1,\quad\mathrm{T}(A_2)=B_2,\quad \mathrm{T}(A_3)=B_3,\quad\ldots, $$ то пишут $$ \begin{gather*} \overrightarrow{A_1B_1}=\overrightarrow{A_2B_2}= \overrightarrow{A_3B_3}=\ldots=\bm{a},\\ \mathrm{T}=\mathrm{T}_{\overrightarrow{A_1B_1}}= \mathrm{T}_{\overrightarrow{A_2B_2}}= \mathrm{T}_{\overrightarrow{A_3B_3}}=\mathrm{T}_{\bm{a}}. \end{gather*} $$

Логика образования общих понятий нас привела к несколько необычному утверждению: свободный вектор $\bm{a}$‍‍ есть не что иное, как график соответствующего параллельного переноса $\mathrm{T}_{\bm{a}}$‍‍ на вектор $\bm{a}$‍‍. Будет хорошо, ecли вы полностью разберётесь в том, что этот вывод является неизбежным следствием принятых нами определений графика, свободного вектора (как множества равных по длине и направлению связанных векторов) и связанного вектора (как пары точек). Замечу, впрочем, что такие определения связанного вектора и свободного вектора не вполне общеприняты, хотя и представляются автору этой статьи самыми удобными.

Задачи

1. Напоминание и небольшие дополнения

1. Какова область определения функций $$ 1)~f_1(x)=\dfrac x{x-|x|},\quad 2)~f_2(x)=\dfrac{\sqrt{1-x}}{\sqrt{1+x^2}},\quad 3)~f_3(x)=\dfrac{x^4-1}{x^2-1}? $$
2. Какое условие надо добавить к формуле $$ f(x)=x^2+1, $$ чтобы она определила функцию $f_3$‍‍ из задачи 1?
3. Какое дополнительное условие надо добавить к формуле $$ f()=1, $$ чтобы получилось определение функции $$ f_4(x)=(\sqrt{x\vphantom1})^2+(\sqrt{1-x})^2? $$

Замечание. В задачах 1‍—‍3 под знаком $\sqrt{~}$‍‍ понимается «арифметический» квадратный корень, т. е. неотрицательное число.

2. График функции

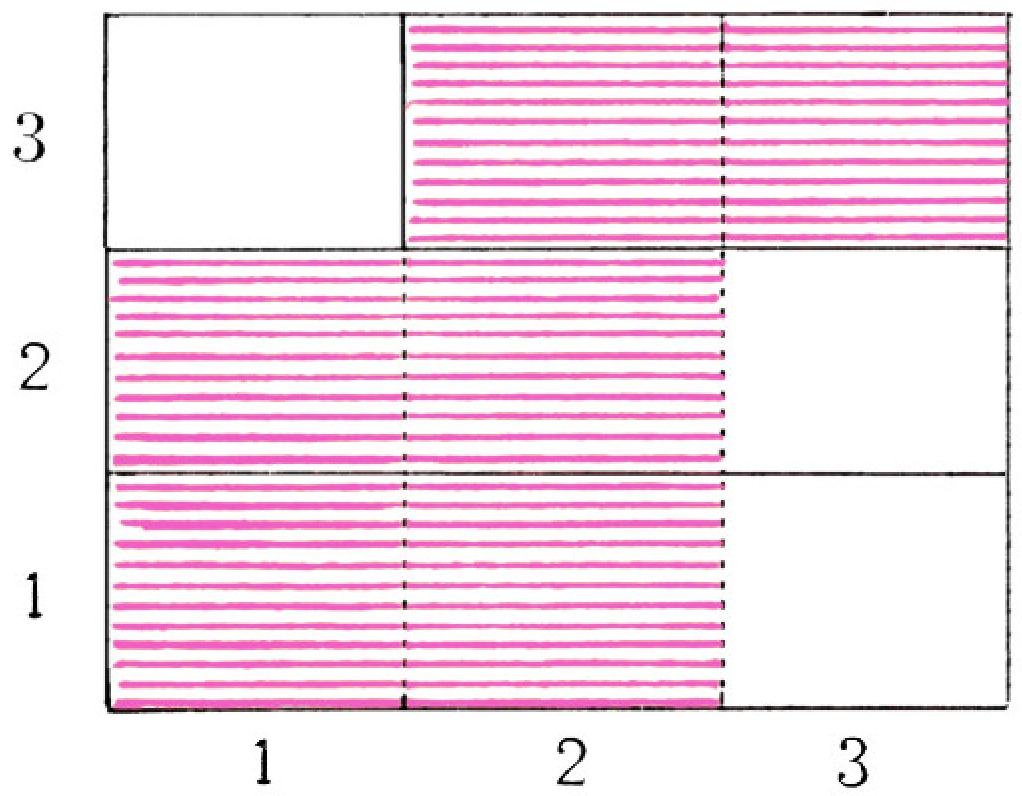
4. Сколько существует функций с областью определения $\{1,2,3\}$‍,‍ графики которых являются подмножествами множества пар $$ \{(1,1),(1,2),(2,1),(2,2),(2,3),(3,3)\} $$ (см. рис. 6)? Сколько из этих функций имеет обратную?
5. Покажите, что график обратной функции $f^{-1}$‍‍ определяется формулой $$ \Gamma_{f^{-1}}=\{(x,y)\mid (y,x)\in\Gamma_f\}. $$ (Естественно, предполагается, что функция $f$‍‍ имеет обратную.)

3. Числовая плоскость

6. Опишите устройство графика функции Дирихле: $$ D(x)=\begin{cases} 1,&\text{если}~x~\text{рационально},\\ 0,&\text{если}~x~\text{иррационально.}\end{cases} $$

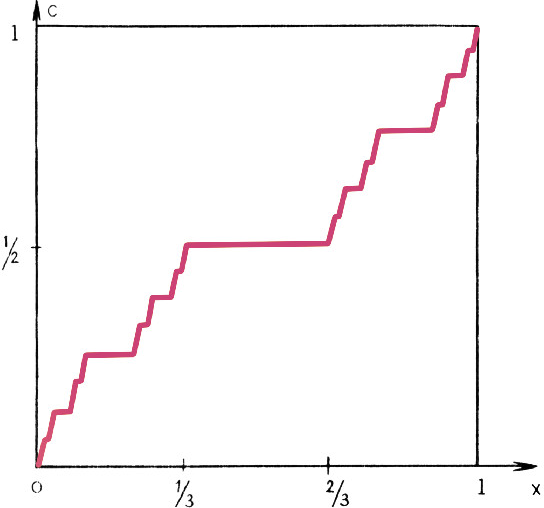
7. Число $x$‍‍ из отрезка $[0;1]$‍‍ разлагается в бесконечную троичную дробь $$ x=0{,}x_1x_2x_3\ldots\quad(x_n=0,1,2). $$

   Значение функции $y=C(x)$‍‍ определяется двоичной дробью $$ y=0{,}y_1y_2y_3\ldots\quad(y_n=0,1) $$ следующим образом: $$ \begin{gather*} \begin{aligned} \text{если}~x_n&=0{,}~\text{то}~y_n=0,\\ \text{если}~x_n&=1~\text{или}~x_n=2{,}~\text{то:} \end{aligned}\\[9pt] \begin{aligned} y_n=1~&\text{при условии, что среди цифр}\\ &x_1{,}~x_2{,}~{\ldots}{,}~x_{n-1}~\text{не было единиц},\\ y_n=0~&\text{при условии, что среди цифр}\\ &x_1{,}~x_2{,}~{\ldots}{,}~x_{n-1}~\text{уже встречалась одна единица}. \end{aligned} \end{gather*} $$

   Попробуйте начертить график этой функции. Докажите, что он содержит бесконечное число горизонтальных отрезков. Если вы знакомы с понятием непрерывности функции, попробуйте доказать, что наша функция непрерывна.

   Замечание. В этой задаче мы не избегаем троичных дробей, в которых все знаки, начиная с некоторого, двойки, и двоичных дробей, в которых все знаки, начиная с некоторого, единицы. Например, мы пишем в троичной системе $$ 0{,}2222\ldots=1;\quad 0{,}12222\ldots=0{,}200000\ldots $$ и в двоичной системе считаем, что $$ 0{,}1111111\ldots=1;\quad 0{,}01011111\ldots=0{,}01100000\ldots $$

4. Геометрические преобразования

8. Опишите в геометрических терминах преобразования числовой плоскости, которые аналитически задаются формулами: $$ \begin{align*} \text{а)}~~&(x,y)\to(-y,x),\\ \text{б)}~~&(x,y)\to(x,-y),\\ \text{в)}~~&(x,y)\to(y,-x),\\ \text{г)}~~&(x,y)\to(-x,y),\\ \text{д)}~~&(x,y)\to(x+1,y),\\ \text{е)}~~&(x,y)\to(x+a,y+a). \end{align*} $$
9. Докажите для поворотов вокруг общего центра $O$‍‍ формулу $$ \mathrm{R}_O^\alpha[\mathrm{R}_O^\beta(P)]=\mathrm{R}_O^{\alpha+\beta}(P). \tag1 $$
10. Докажите, что при любых центрах $O_1$‍‍ и $O_2$‍‍ преобразование $$ F(P)=\mathrm{R}_{O_1}^\alpha[\mathrm{R}_{O_2}^{-\alpha}(P)] $$ будет параллельным переносом. На какое расстояние и в каком направлении?

5. Векторы

11. Докажите формулу $$ \mathrm{T}_{\bm{a}}[\mathrm{T}_{\bm{b}}(P)]=\mathrm{T}_{\bm{a}+\bm{b}}(P). \tag2 $$
12. Покажите, что преобразование $$ F(P)=\mathrm{T}_{\bm{a}}[\mathrm{R}_O^\alpha(P)] $$ является поворотом на угол $\alpha$‍.‍ Вокруг какого центра?

Замечание. Формулы (1) и (2) короче пишут $$ \begin{gather*} \mathrm{R}_O^\alpha\mathrm{R}_O^\beta=\mathrm{R}_O^{\alpha+\beta},\\[3pt] \mathrm{T}_{\bm{a}}\mathrm{T}_{\bm{b}}=\mathrm{T}_{\bm{a}+\bm{b}}. \end{gather*} $$

Взятие функции от функции во многих отношениях похоже на умножение. Но это уже особая тема, разработка которой не умещается в этой статье. Мы воспользуемся такой короткой записью функции от функции (композиции отображений) в задачах 13 и 14.

13. Докажите, что всегда $$ \mathrm{T}_{\bm{a}}\mathrm{T}_{\bm{b}}=\mathrm{T}_{\bm{b}}\mathrm{T}_{\bm{a}} $$ и $$ \mathrm{R}_O^\alpha\mathrm{R}_O^\beta=\mathrm{R}_O^\beta\mathrm{R}_O^\alpha $$ при поворотах вокруг общего центра. Покажите на примере, что, вообще говоря, $$ \mathrm{R}_{O_1}^\alpha\mathrm{R}_{O_2}^\beta\ne \mathrm{R}_{O_2}^\beta\mathrm{R}_{O_1}^\alpha $$ при поворотах вокруг различных центров $O_1$‍,‍ $O_2$‍.‍
14. Выясните полностью вопрос о том, когда всё-таки $$ \mathrm{R}_{O_1}^\alpha\mathrm{R}_{O_2}^\beta= \mathrm{R}_{O_2}^\beta\mathrm{R}_{O_1}^\alpha. $$