Башмаков М. И.

Геометрические неравенстваБашмаков М. И. Геометрические неравенства // Квант. — 1970. — № 2. — С. 23‍—‍25.‍‍

На страницах нашего журнала начинает свою работу математический кружок. Темы его занятий будут в основном доступны уже восьмиклассникам, но мы надеемся, что они будут интересны всем читателям «Кванта».
Первое занятие кружка посвящается геометрическим неравенствам.

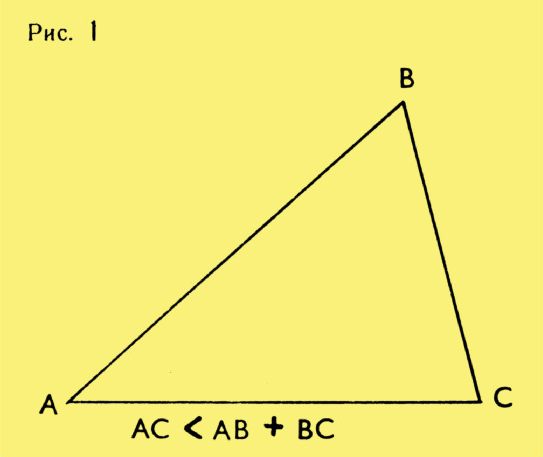
В самом начале изучения геометрии мы знакомимся с важным фактом: сторона треугольника меньше суммы двух других сторон (рис. 1). Одно это неравенство, которое называют неравенством треугольника, позволяет решить ряд интересных геометрических задач.

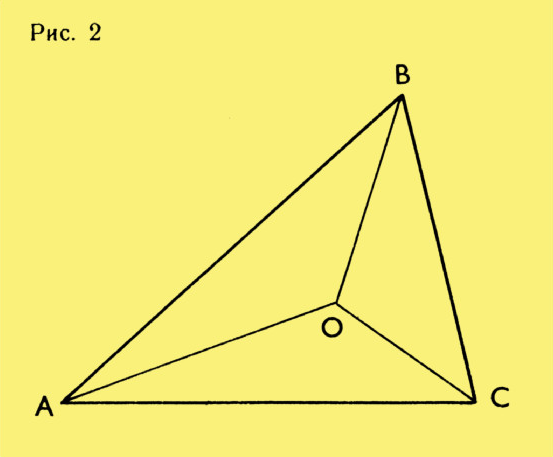
Задача 1. Докажите, что сумма расстояний от любой точки, лежащей внутри треугольника, до его вершин больше половины периметра этого треугольника.

Решение. Рассмотрим треугольники $AOB$‍,‍ $BOC$‍‍ и $COA$‍‍ (рис. 2) и напишем три неравенства треугольника: $$ \begin{align*} AO+OB&\gt AB,\\ BO+OC&\gt BC,\\ CO+OA&\gt CA. \end{align*} $$ Складывая эти неравенства и деля пополам, получим $$ AO+BO+CO\gt\dfrac12(AB+BC+CA), $$ что и требовалось доказать.

Попробуйте решить самостоятельно ещё несколько задач на доказательство неравенств. Надо разумно выбирать треугольники, выписывать неравенства для их сторон и преобразовывать эти неравенства к нужному виду.

Докажите, что:

Задача 2. Сумма диагоналей выпуклого пятиугольника меныше удвоенного периметра.

Задача 3. Сумма диагоналей выпуклого пятиугольника больше периметра.

Задача 4. Медиана треугольника меньше полусуммы сторон, между которыми она заключена.

Задача 5. Сумма медиан треугольника меньше периметра, но больше трёх четвертей периметра.

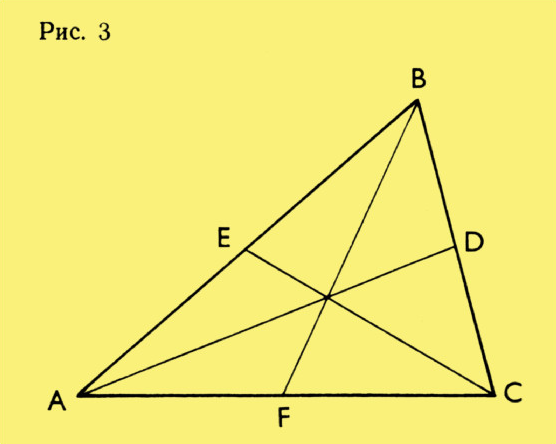
Вы, наверное, обратили внимание на то, что в каждой задаче приходится по-своему выбирать, каким способом, в какую сторону проводить оценку (устанавливать неравенство). При этом не всегда удаётся сразу получить нужный результат. Например, в последней задаче легко получить, что сумма медиан больше половины периметра. (Достаточно рассмотреть треугольники $ABD$‍,‍ $BCF$‍‍ и $CAE$‍‍ на рис. 3.) В то же время из других треугольников можно получить более точную оценку, требуемую в задаче. Возникает вопрос: какова наибольшая константа $k_1$‍,‍ для которой верна оценка $$ k_1p\lt m_a+m_b+m_c? $$ (Здесь $m_a$‍,‍ $m_b$‍,‍ $m_c$‍‍ — медианы к сторонам $a$‍,‍ $b$‍‍ и $c$‍,‍ а $p$‍‍ — периметр треугольника.) Точно так же, интересно получить точную оценку и сдругой стороны: найти наименьшую константу $k_2$‍,‍ для которой неравенство $$ m_a+m_b+m_c\lt k_2p $$ верно для любого треугольника.

Задача 6. Докажите, что при сравнении суммы медиан треугольника с его периметром лучшими (т. е. крайними) константами будут $k_1=\dfrac34$‍‍ и $k_2=1$‍.‍ Более точно: докажите, что отношение $$ x=\dfrac{m_a+m_b+m_c}p $$ принимает все значения между $\dfrac34$‍‍ и 1.

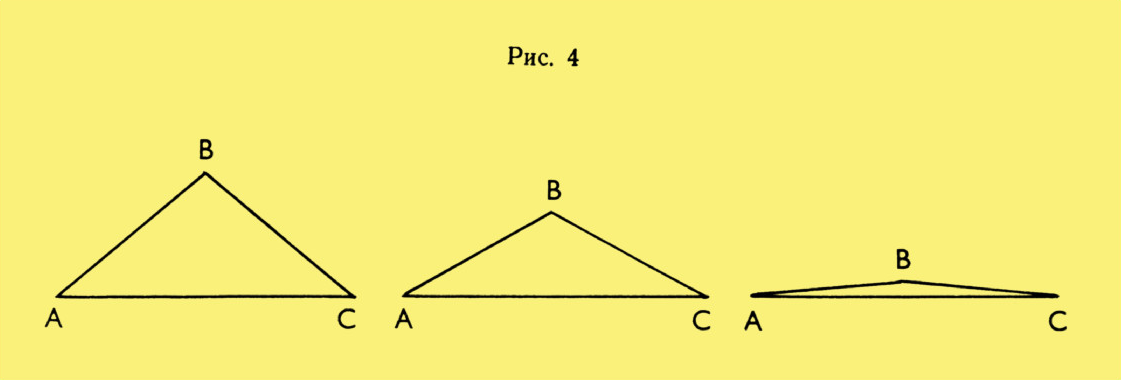
Обратим внимание на то, что нeравенства во всех предыдущих задачах были строгие. Если мы хотим приблизиться к границе, т. е. искать треугольники, для которых неравенство близко к равенству, мы должны и треугольники выбирать близкие к «вырожденным». Так, чтобы показать неулучшаемость оценки $$ m_a+m_b+m_c\gt\dfrac34p, $$ можно рассмотреть, например, такие равнобедренные треугольники, вершины которых приближаются к основанию (рис. 4). Ясно, что их периметр близок к удвоенной стороне основания, а сумма медиан близка к $\dfrac32$‍‍ основания. Равенство получится, когда вершина упадёт на основание, а треугольник «выродится» в двойной отрезок.

Вообще, для любого числа $x$‍‍ из интервала $$ \dfrac34\lt x\lt1 $$ можно указать такой равнобедренный треугольник, для которого $$ \dfrac{m_a+m_b+m_c}p=x. $$ Это позволяет решить задачу 6.

Задача 7. Докажите, что сумма расстояний любой точки внутри треугольника до его вершин меньше периметра.

Задача 8. Сравните задачи 1 и 7, 2 и 3; поставьте и исследуйте вопрос, аналогичный тому, который мы обсуждали относительно медиан.

Задача 9. Рассмотрим всевозможные выпуклые $n$‍‍-угольники ($n$‍‍ — определённое число). Возьмём точку внутри такого многоугольника и составим отношение суммы её расстояний до вершин к периметру. Какие значения это отношение может принимать?‍

В следующих задачах нужно использовать, кроме неравенства треугольника, некоторые другие простые неравенства, например то, что из двух сторон треугольника больше та, которая лежит против большего угла, в частности, что гипотенуза прямоугольного треугольника больше катета, и т. п.

Задача 10. Докажите, что для всех прямоугольных треугольников верны следующие неравенства: $0{,}4\lt\dfrac rh\lt 0{,}5$‍,‍ где $r$‍‍ — радиус вписанного круга, $h$‍‍ — высота, опущенная из вершины прямого угла. Являются ли написанные границы точными?

Задача 11. На биссектрисе внешнего угла $C$‍‍ треугольника $ABC$‍‍ берётся точка $M$‍,‍ отличная от $C$‍.‍ Докажите, что сумма её расстояний до вершин $A$‍‍ и $B$‍‍ больше, чем сумма расстояний от точки $C$‍‍ до этих же вершин.

Задача 12. Для того чтобы угол $A$‍‍ в треугольнике $ABC$‍‍ был острым, необходимо и достаточно, чтобы медиана, проведённая из вершины $A$‍,‍ была более чем вдвое больше стороны $BC$‍.‍

Задача 13. В остроугольном треугольнике $ABC$‍‍ наибольшая из высот (обозначим её через $AH$‍)‍ равна медиане $BM$‍.‍ Докажите, что угол $ABC$‍‍ меньше $60^\circ$‍.‍

Задача 14. На продолжении наибольшей стороны $AC$‍‍ треугольника $ABC$‍‍ отложен отрезок $CO=BC$‍.‍ Докажите, что угол $ABO$‍‍ тупой.

Задача 15. $A$‍,‍ $B$‍,‍ $C$‍,‍ $D$‍‍ — последовательные вершины выпуклого четырёхугольника $ABCD$‍.‍ Докажите, что если $$ AB+BD\le AC+CD, $$ то $$ AB\le AC. $$

Литература

Делоне Б., Житомирский О. Задачник по геометрии. — М.: Физматгиз, 1959.

Скопец З. А., Жаров В. А. Задачи и теоремы по геометрии. Планиметрия. — М.: Учпедгиз, 1962.

Сивашинский И. Е. Неравенства в задачах.