Изображения страниц
Текст статьи Слободецкий И. Ш. Сухое трение // Квант. — 1970. — № 1. — С. 37—43.
Почему при резком торможении автомобиль заносит?
Почему скрипит плохо смазанная дверь?
Почему движущийся равномерно смычок
заставляет звучать скрипичную струну?
Всё это объясняется свойствами силы трения,
о которых и идёт речь в этой статье.
С трением мы сталкиваемся на каждом шагу. Вернее было бы сказать, что без трения мы и шагу ступить не можем. Но несмотря на ту большую роль, которую играет трение в нашей жизни, до сих пор не создана достаточно полная картина возникновения трения, и вопрос этот остаётся неясным. Это связано даже не с тем, что трение имеет сложную природу, а скорее с тем, что опыты с трением очень чувствительны к обработке поверхности и поэтому трудно воспроизводимы.
Вот пример. Английский физик Гарди исследовал зависимость силы трения между стеклянными пластинками от температуры. Он тщательно обрабатывал пластинки хлорной известью и обмывал их водой, удаляя жиры и загрязнения. Трение увеличивалось с температурой. Опыт был повторён много раз, и каждый раз получались примерно одни и те же результаты. Но однажды, мóя пластинки, Гарди протёр их пальцами. Трение перестало зависеть от температуры. Протерев пластинки, Гарди, как он сам считает, удалил с них очень тонкий слой стекла, изменивший свои свойства из-за взаимодействия с хлоркой и водой.
Когда говорят о трении, различают три отличных физических явления: сопротивление при движении тела в жидкости или газе — его называют жидким трением; сопротивление, возникающее, когда тело скользит по какой-нибудь поверхности, — трение скольжения, или сухое трение; и сопротивление, возникающее, когда тело катится, — трение качения. Эта статья посвящена сухому трению.
Первые исследования трения, о которых мы знаем, были проведены Леонардо да Винчи примерно 450 лет назад. Он измерял силу трения, действующую на деревянные параллелепипеды, скользящие по доске, причём, ставя бруски на разные грани, определял зависимость силы трения от площади опоры. Но работы Леонардо да Винчи не были опубликованы. Они стали известны уже после того, как классические законы трения были в 17—18 в.в. вновь открыты французскими учёными Амонтоном и Кулоном.
Вот эти законы:
- сила трения
$F$ прямо пропорциональна силе$N$ нормального давления тела на поверхность, по которой движется тело:$F=kN$, где$k$ — безразмерный коэффициент, называемый коэффициентом трения; - сила трения не зависит от площади контакта между поверхностями;
- коэффициент трения зависит от свойств трущихся поверхностей;
- сила трения не зависит от скорости движения тела.
Триста лет исследований трения подтвердили правильность трёх первых законов, предложенных Амонтоном и Кулоном. Неверным оказался лишь последний — четвёртый. Но это стало ясно много позже, когда появились железные дороги и машинисты заметили, что при торможении состав ведёт себя не так, как предсказывали инженеры.
Амонтон и Кулон объясняли происхождение трения довольно просто. Обе поверхности неровные, они покрыты небольшими горбами и впадинами. При движении выступы цепляются друг за друга, и поэтому тело всё время поднимается и опускается. Для того чтобы втащить тело на «холмы», к нему нужно приложить определённую силу. Если выступы большие, то и сила нужна побольше. Но это объяснение противоречит одному очень существенному явлению: на трение тратится энергия. Кубик, скользящий по горизонтальной поверхности, останавливается. Его энергия расходуется на трение. А поднимаясь и опускаясь, тело не тратит своей энергии. Вспомните аттракцион «американские горы». Когда санки скатываются с горки, их потенциальная энергия переходит в кинетическую, и скорость санок возрастает, а когда санки въезжают на новую возвышенность, кинетическая энергия, наоборот, переходит в потенциальную. Энергия санок уменьшается за счёт трения, но не из-за подъёмов и спусков. Аналогично обстоит дело и при движении одного тела по поверхности другого. Здесь потери энергии на трение также не могут быть связаны с тем, что выступы одного тела взбираются на бугры другого.
Есть ещё возражения. Например, простые опыты по измерению силы трения между полированными стеклянными пластинками показали, что при улучшении полировки поверхностей сила трения сначала не меняется, а затем возрастает, а не убывает, как следовало бы ожидать на основании модели явления, предложенной Амонтоном и Кулоном.
Механизм трения значительно более сложен. Из-за неровностей поверхностей они соприкасаются только в отдельных точках на вершинах выступов. Здесь молекулы соприкасающихся тел подходят на расстояния, соизмеримые с расстоянием между молекулами в самих телах, и сцепляются. Образуется прочная связь, которая рвётся при нажиме на тело. При движении тела связи постоянно возникают и рвутся. При этом возникают колебания молекул. На эти колебания и тратится энергия.
Площадь действительного контакта составляет обычно от одного до двух тысяч квадратных микронов. Она практически не зависит от размеров тела и определяется природой поверхностей, их обработкой, температурой и силой нормального давления. Если на тело надавить, то выступы сминаются, и площадь действительного контакта увеличивается. Увеличивается и сила трения.
При значительной шероховатости поверхностей большую роль в увеличении силы трения начинает играть механическое зацепление между «холмами». Они при движении сминаются, и при этом тоже возникают колебания молекул.
Теперь понятен опыт с полированными стеклянными пластинками. Пока поверхности были «грубые», число контактов было невелико, а после хорошей полировки оно возросло. Можно привести ещё пример увеличения трения с улучшением поверхности. Если взять два металлических бруска с чистыми полированными поверхностями, то они слипаются. Трение здесь становится очень большим, так как площадь действительного контакта велика. Силы молекулярного сцепления, которые ответственны за трение, превращают два бруска в монолит!
В домашних условиях можно провести следующий опыт. Поставьте рюмку на стеклянную пластинку и, привязав к ножке бечёвку, потащите рюмку. Затем увлажните стекло и ножку рюмки водой, которая смоет жиры и грязь. Опять потащите. Теперь это сделать значительно труднее. Чистый контакт стекло—стекло разорвать нелегко. Присмотревшись к поверхности, вы можете заметить даже царапины. Вырвать кусочки стекла оказывается легче, чем разорвать контакт!
Рассмотренная нами модель трения довольно груба. Мы не останавливались
здесь на диффузии молекул, т. е. на проникновении молекул одного тела в другое, на роли электрических зарядов, возникающих на соприкасающихся
поверхностях, на роли и механизме действия смазки. Эти вопросы во многом
неясны, а объяснения спорны. Можно только удивляться тому, что при такой
сложности трение описывается столь простым законом:
Сухое трение имеет одну существенную особенность: трение покоя. Если в жидкости или газе трение возникает только при движении тела и тело можно
сдвинуть, приложив к нему даже очень маленькую силу, то при сухом трении
тело начинает двигаться только тогда, когда проекция приложенной к нему силы
Часто об этом забывают при решении задач. На вопрос «какая сила трения действует на стол весом 30 кг, стоящий на полу, если коэффициент трения равен 0,4», большинство уверенно отвечает: «12 кг», что неверно. Сила трения равна нулю, иначе стол поехал бы в сторону действия силы трения, так как других горизонтальных сил нет.
Итак, если тело покоится, то для того, чтобы сдвинуть его с места, к телу нужно приложить силу, большую максимально возможной силы трения покоя, которое обусловлено прочностью молекулярных связей. А как обстоит дело, если тело уже движется? Какую силу нужно приложить для того, чтобы тело начало двигаться ещё и в другом направлении? Оказывается, сколь угодно малую. Связано это как раз с тем, что сила трения не может быть больше максимальной силы трения покоя.
Попробуйте проделать простой опыт. Возьмите книжку и положите её одним краем на другую книжку потолще. Получится наклонная плоскость. Теперь положите на эту плоскость спичечный коробок, к которому привязана нитка. Если коробок скользит, то уменьшите наклон плоскости, взяв книжку-подставку потоньше. Потяните за нитку коробок вбок. При этом он поедет ещё и вниз! Уменьшите наклон плоскости и опять потяните за нитку. Та же картина. Коробок соскальзывает даже при очень малых углах наклона плоскости. Сила трения, раньше удерживавшая коробок на плоскости, стала почему-то очень маленькой.
Попробуем понять, в чём здесь дело. Если бы коробок двигался только
горизонтально, то параллельно ребру наклонной плоскости на него действовала
бы сила трения, равная
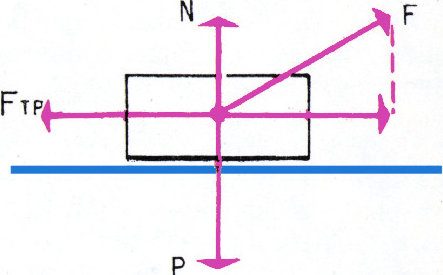
Возьмём брусок, привяжем к нему нить и, положив брусок на горизонтальную
плоскость, будем тянуть за нить с постоянной скоростью
Составляющая
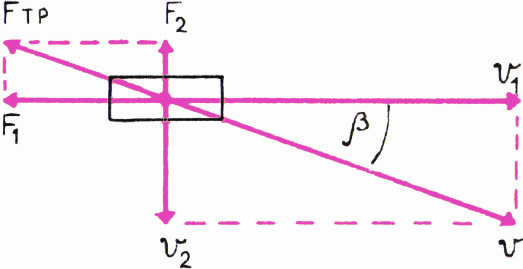
Любопытный вывод можно теперь сделать для коробка, движущегося по наклонной плоскости. Здесь
При малых углах наклона плоскости к горизонту (таких, что
Этот вывод легко проверить экспериментально. Так как при равномерном
движении путь, пройденный телом, пропорционален скорости, то отношение
скорости
Явление, о котором шла речь, совсем нередкое и встречается довольно часто. Например, известно, что при резком торможении электродвигателя ремень передачи часто соскальзывает со шкивов. Происходит это потому, что при торможении двигателя ремень начинает проскальзывать относительно шкивов, и достаточно небольшой силы, чтобы сдвинуть ремень вбок. Так как обычно имеется небольшой перекос в установке шкивов и ремня, то такой силой является составляющая силы натяжения ремня. Вот ещё примеры. Когда хотят вытащить гвоздь из стенки без помощи клещей, его сгибают и тащат, поворачивая одновременно вокруг оси. По той же причине при резком торможении автомобиль теряет управление: машину «заносит». Колёса скользят по дороге, а боковая сила возникает за счёт неровностей дороги.
Остановимся теперь на последнем законе Амонтона — Кулона: сила трения не зависит от скорости тела. Это не совсем так.
Вопрос о зависимости силы трения от скорости имеет очень важное практическое значение. И хотя эксперименты здесь имеют много специфических трудностей, они окупаются использованием полученных сведений, например, в теории резания металлов, в расчётах движения пуль и снарядов в стволе и т. д.
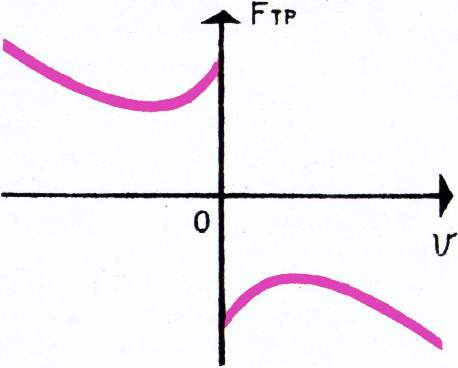
Обычно считают, что для того, чтобы сдвинуть тело с места, к нему нужно приложить бо́льшую силу, чем для того, чтобы тащить тело. В большинстве случаев это связано с загрязнениями поверхностей трущихся тел. Например, для чистых металлов такого скачка силы трения не наблюдается. Опыты с движением пули в стволе показали, что с увеличением скорости пули величина силы трения сначала быстро убывает, затем она уменьшается всё медленнее, а при скоростях, больших 100 м/с, начинает возрастать. График зависимости силы трения от скорости показан на рисунке. Грубо это можно объяснить тем, что в месте контакта выделяется много тепла. При скоростях порядка 100 м/с температура в месте контакта может достигать нескольких тысяч градусов, и между поверхностями образуется слой расплавленного металла. Трение становится жидким. При больших же скоростях жидкое трение пропорционально квадрату скорости.
Интересно, что примерно такую же зависимость от скорости имеет сила трения смычка о струну. Именно поэтому мы можем слушать игру на смычковых инструментах — скрипке, виолончели, альте.
При равномерном движении смычка струна увлекается им и натягивается. Вместе с натяжением струны увеличивается сила трения между смычком и струной. Когда величина силы трения становится максимально возможной, струна начинает проскальзывать относительно смычка. Если бы сила трения не зависела от относительной скорости смычка и струны, то, очевидно, отклонение струны от положения равновесия не изменялось бы.
Но при проскальзывании трение уменьшается. Поэтому струна начинает двигаться к положению равновесия. При этом относительная скорость струны увеличивается, а это ещё уменьшает силу трения. Когда же струна, совершив колебание, движется в обратном направлении, её скорость относительно смычка уменьшается, и смычок опять захватывает струну. Всё повторяется. Так возбуждаются колебания струны. Эти колебания незатухающие, так как энергия, потерянная струной при её движении, каждый раз восполняется работой силы трения, подтягивающей струну до положения, при котором струна срывается.
Этим можно и закончить статью о сухом трении — явлении, природу которого мы ещё не понимаем достаточно хорошо, но умеем описывать с помощью законов, выполняющихся с удовлетворительной точностью. Это даёт нам возможность объяснять многие физические явления и делать расчёты, необходимые при постройке машин.
Задачи
- Почему автомобиль поворачивает, когда поворачивают его передние колёса?
- Положите горизонтально палку на вытянутые указательные пальцы. Медленно передвигайте правую руку к левой. Почему при этом палка тоже передвигается, причём так, что её равновесие не нарушается?
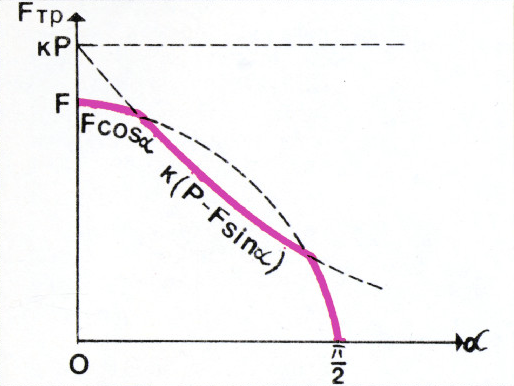
- Нарисуйте график зависимости силы трения, действующей на брусок, находящийся на наклонной плоскости, от угла наклона плоскости к горизонту.
- Нарисуйте график зависимости силы трения, действующей на брусок,
находящийся на горизонтальной поверхности, от угла, который составляет
приложенная к этому бруску сила с горизонтом. Приложенная к бруску сила
меньше веса бруска, а угол меняется от 0 до
$\dfrac\pi2$. -
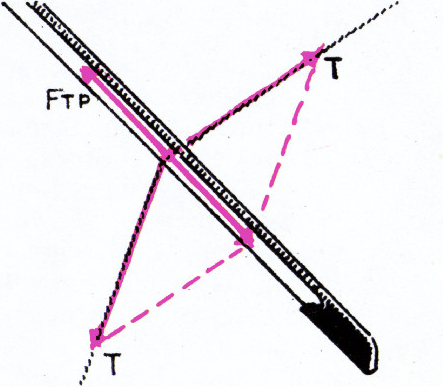
Оборвавшиеся при бурении трубы можно поднимать с помощью устройства,
показанного на рисунке. Стержни
$AB$ и$AC$ шарнирно прикреплены к тросу в точке$A$. Подъём трубы осуществляется за счёт трения стержней о трубу. Найдите условие, при котором с помощью подобного устройства можно поднимать трубы любого веса. Трос, конечно, достаточно прочен.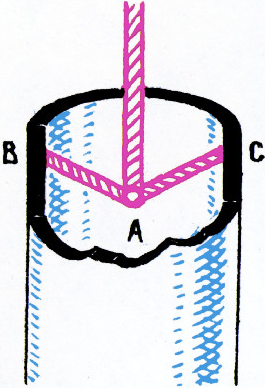
- Небольшой кубик массы
$m$ лежит на шероховатой плоскости, наклонённой к горизонту под углом$\alpha$. Коэффициент трения$k=2\tg\alpha$. Определите минимальную горизонтальную силу$F$ (см. рисунок), с которой нужно толкать кубик, чтобы он начал двигаться.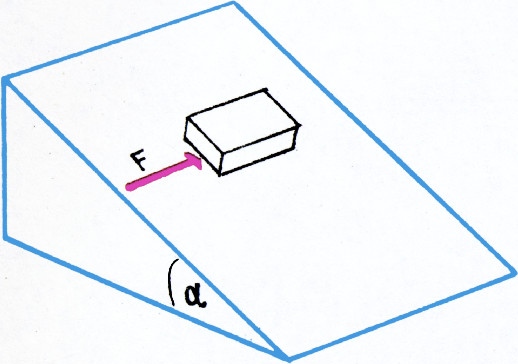
- Маховик радиуса
$R=20~\text{см}$ насажен на горизонтальную ось радиуса$r=2~\text{см}$. Закрепив ось, маховик можно снять, если его потянуть с силой$F=100~\text{кг}$. Для того чтобы снять маховик было легче, к его ободу прикладывают силу$F_1=8~\text{кг}$, создающую вращательный момент относительно оси. С какой минимальной силой$F_2$ нужно при этом тянуть маховик вдоль оси? - Почему скрипит плохо смазанная дверь?
Ответы, указания, решения
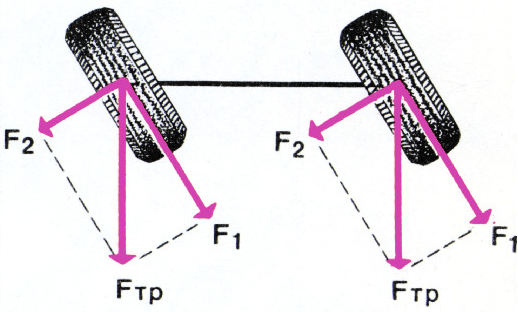
- Разложим силы трения, действующие на передние колёса автомобиля, на две составляющие:
$F_1$, лежащие в плоскости колёс, и$F_2$, перпендикулярные колёсам (см. рисунок). Силы$F_1$, заставляют колёса вращаться, а силы$F_2$ поворачивают автомобиль. - Если центр тяжести палки не находится посередине между пальцами, то давление палки на пальцы различно. Различны и силы трения, действующие на палку со стороны пальцев. Палка смещается в ту сторону, где трение меньше.
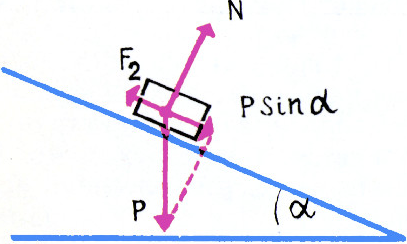
Пока брусок не скользит по плоскости, сила трения равна по величине проекции веса бруска на наклонную плоскость
$F_{\text{тр}}=P\sin\alpha$. Брусок начинает скользить, когда сила трения достигает максимальной величины трения покоя$F_{\text{тр}}=kN=kP\cos\alpha$. При этом выполняется условие$kP\cos\alpha=P\sin\alpha$. Поэтому соскальзывание бруска начинается при угле наклона плоскости к горизонту$\alpha=\arctg k$. После этого сила трения будет равна$F_{\text{тр}}=kP\cos\alpha$. 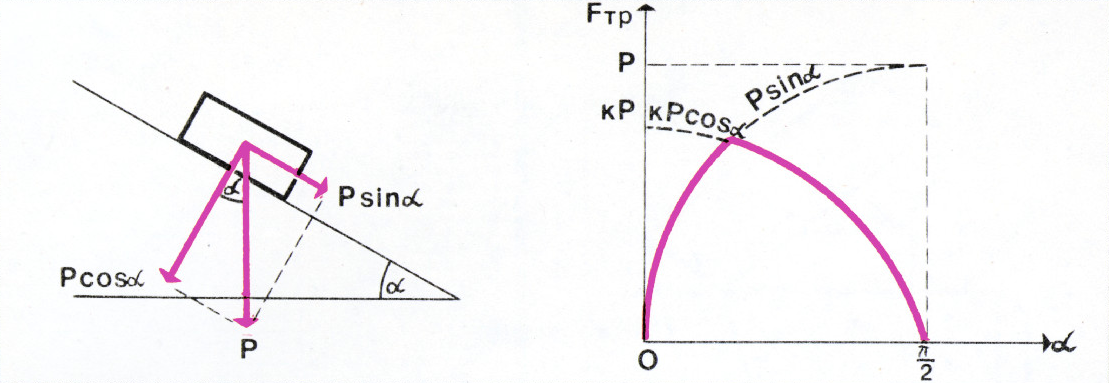
Угол
$\alpha=\arctg k$, при котором брусок начинает скользить, называют углом трения. Он имеет ещё и другой геометрический смысл: если к бруску, лежащему на горизонтальной плоскости, приложить силу, составляющую с вертикалью угол меньший, чем угол трения, то брусок нельзя сдвинуть с места, сколь велика ни была бы приложенная сила. Доказать это можно так. Посадим наблюдателя на наклонную плоскость, на которой лежит брусок, и будем увеличивать угол наклона плоскости к горизонту. Наблюдатель скажет, что в его системе координат на тело, лежащее на плоскости, которую он считает горизонтальной, действует сила, составляющая с перпендикуляром к плоскости угол$\alpha$. Если$\tg\alpha\le k$ (т. е.$\alpha\lt\arctg k$), то брусок не скользит по плоскости, сколь бы велика ни была приложенная сила.- Ответ показан на рисунке.
Трос действует на стержни с силами
$F_1$ и$F_2$, величина которых зависит от веса трубы. Направлены эти силы вдоль стержней. Поэтому, если стержни составляют с перпендикуляром к поверхности трубы угол меньший, чем$\alpha=\arctg k$ ($k$ — коэффициент тpeния стержней о трубу), то стержни не будут скользить по трубе, сколь бы велики ни были силы$F_1$ и$F_2$, а значит, каким бы большим ни был вес трубы (см. решение задачи 3). В подобных случаях инженеры говорят о заклинивании.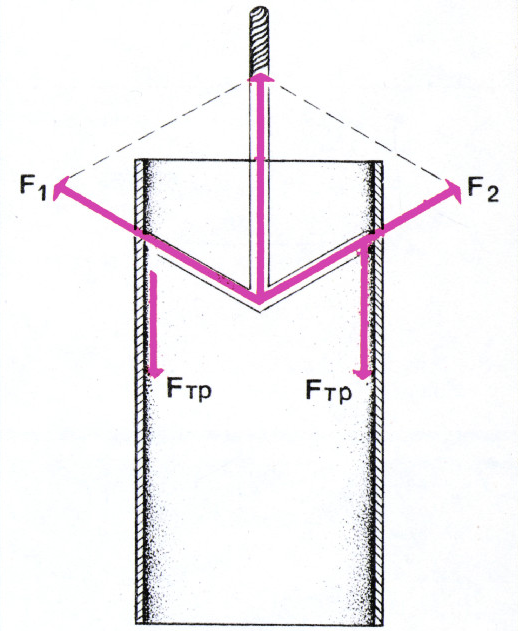
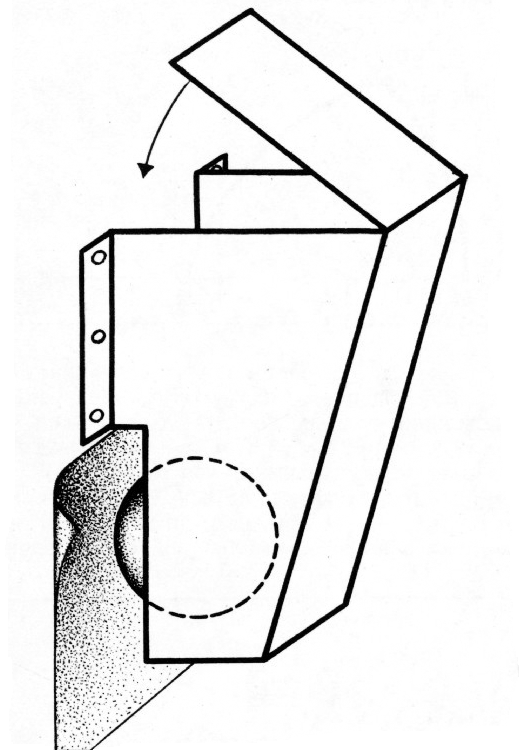
Используя заклинивание, можно сделать простой и удобный замок для подвешивания карт и чертежей. Нужно изготовить две металлические обоймы, как показано на рисунке, и, прибив обоймы к доске, вложить в них по шарику.
Вставленный в прорезь чертёж прижмётся шариком к доске. Если угол
$\alpha$, образуемый наклонной гранью обоймы с вертикалью, таков, что$\tg2\alpha\lt k$ (где$k$ — коэффициент трения между шариком и чертежом), то чертёж будет удерживаться силой трения о шарик, каким бы большим ни был вес чертежа и каким бы малым ни было трение чертежа о доску. Для того чтобы вытащить чертёж из замка, достаточно приподнять шарик указкой.- Кубик начнёт скользить, когда равнодействующая силы
$F$ и составляющей веса кубика, параллельной наклонной плоскости,$P\sin\alpha$ не станет равна максимальной силе трения покоя: $$ kP\cos\alpha=\sqrt{P^2\sin^2\alpha+F^2}. $$ Отсюда $$ F=\sqrt{k^2P^2\cos^2\alpha-P^2\sin^2\alpha}=\sqrt3\,P\sin\alpha. $$ - 60 кг.
- Скрип двери объясняется так же, как звучание струны.











