Бескин Н. М.

Цепные дробиБескин Н. М. Цепные дроби // Квант. — 1970. — № 1. — С. 16‍—‍26.‍‍

I. Две загадки

1. Загадка Архимеда. Многие полагают: чтобы найти что-нибудь необыкновенное, надо отправиться очень далеко, лучше всего в космос. В обыденной жизни вокруг нас всё хорошо известно, и ничего интересного нет.

Какое заблуждение! Мы окружены загадочными явлениями, но не задумываемся над ними, потому что они привычны. Здесь будет рассказано о двух загадочных фактах из истории математики.

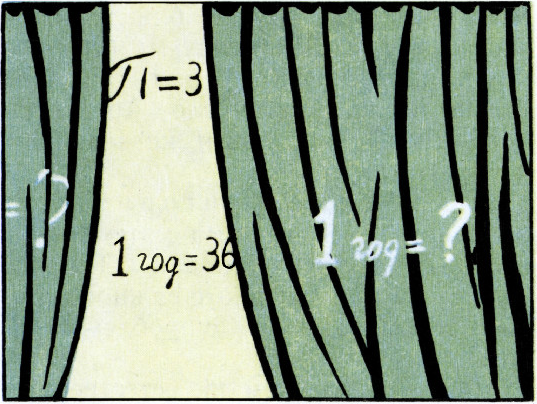
Все школьники мира «проходят» в курсе геометрии, что Архимед нашёл для числа $\pi$‍‍ приближённое значение $\dfrac{22}7$‍‍‍. К этому факту так привыкли, что не подозревают, какая тайна в нём скрыта. А между тем стоит только задать естественный вопрос: почему Архимед предпочёл седьмые доли? Почему не восьмые? Попытка ответить на этот вопрос приведёт нас в новую область арифметики.

Уточним задачу «дать приближённое выражение действительного числа $\alpha$‍‍ в виде дроби со знаменателем $q$‍‍». Это значит: из всех дробей со знаменателем $q$‍‍ найти ближайшую к числу $\alpha$‍‍. Если на числовой оси нанесены все дроби со знаменателем $q$‍,‍ то число $\alpha$‍‍ попадает между двумя такими соседними дробями (случай, когда $\alpha$‍‍ совпадает с одной из них, неинтересен) $$\dfrac{p-1}q\lt\alpha\lt\dfrac pq.$$ Из этих двух дробей выбирается та, которая ближе к $\alpha$‍.‍ Например, на рис. 1 точка $\alpha$‍‍ ближе к правому концу отрезка $\left[\dfrac{p-1}q;\dfrac pq\right]$‍,‍ и поэтому следует принять $$\alpha\approx\dfrac pq.$$ Если $\alpha$‍‍ есть середина отрезка $\left[\dfrac{p-1}q;\dfrac pq\right]$‍,‍ то для определённости условимся выбирать его левый конец.

Процесс замены числа $\alpha$‍‍ его приближённым значением называют аппроксимацией (приближением).

Из изложенного понятно, что для аппроксимации числа $\alpha$‍‍ можно пользоваться дробями с любым знаменателем. Выбор знаменателя зависит от нашего желания. Ради технического удобства почти всегда пользуются десятичными дробями. Однако во времена Архимеда десятичные дроби ещё не были изобретены, и Архимед мог выбрать любые доли. Он выбрал седьмые. Почему? Терпение, скоро мы в этом разберёмся.

При аппроксимации действительного числа $\alpha$‍‍ дробью $\dfrac pq$‍‍ возникает погрешность $$ \Delta=\alpha-\dfrac pq $$ (запомним: погрешность есть точное значение минус приближённое). Если приближённое значение взято с недостатком, то погрешность положительна, а если с избытком — отрицательна.

Абсолютная величина погрешности называется абсолютной погрешностью.

Ясно, что при избранном способе аппроксимации абсолютная погрешность не может превышать $\dfrac1{2q}$‍‍ (см. рис. 1): $$ |\Delta|\le\dfrac1{2q}. $$ Число $\dfrac1{2q}$‍‍ есть верхняя граница абсолютной погрешности. При другом способе аппроксимации верхняя граница может быть иной. Например, если бы мы условились всегда брать приближение с недостатком, то она равнялась бы $\dfrac1q$‍.‍

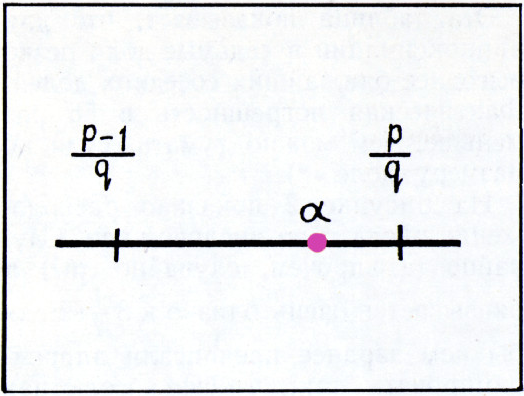
Абсолютная погрешность достигает верхней границы в том (самом неблагоприятном) случае, когда $\alpha$‍‍ есть середина отрезка $\left[\dfrac{p-1}q;\dfrac pq\right]$‍.‍

Ясно, что приближение выгодно, если оно при малом знаменателе $q$‍‍ даёт высокую точность. Чтобы характеризовать выгодность, надо сравнить две величины: 1) фактическую абсолютную погрешность, 2) верхнюю границу абсолютной погрешности: $$ \dfrac{\text{абсолютная погрешность}}{\text{верхняя граница абс. погр.}}= \left|\alpha-\dfrac pq\right|:\dfrac1{2q}=2\cdot|q\alpha-p|. $$

Принято рассматривать половину этой величины. Назовём её приведённой погрешностью $$ h=|q\alpha-p| $$ и запомним: приведённая погрешность $h$‍‍ есть половина отношения фактической абсолютной погрешности к максимально возможной.

Очевидно, $$ 0\lt h\le\dfrac12. $$ Чем меньше $h$‍,‍ тем выгоднее приближение. Если $h$‍‍ близко к нулю, значит, число $\alpha$‍‍ расположено близко к одному из концов отрезка $\left[\dfrac{p-1}q;\dfrac pq\right]$‍.‍ Чем ближе $h$‍‍ к $\dfrac12$‍‍‚ тем $\alpha$‍‍ ближе к середине отрезка.

Величину $$ \lambda=\dfrac1{2h}=\dfrac1{2\cdot|q\alpha-p|} $$ назовём коэффициентом выгодности. Его смысл очень прост: коэффициент выгодности показывает, во сколько раз фактическая абсолютная погрешность менышие максимально возможной. Чем больше $\lambda$‍,‍ тем выгоднее приближение. Очевидно, $$ 1\le\lambda\lt\infty,\quad\lambda h=\dfrac12. $$

Не следует думать, что более мелкие доли всегда дают более точное приближение! Может случиться, что при нанесении на числовую ось восьмых долей число $\alpha$‍‍ занимает менее выгодное положение, чем при нанесении седьмых. Сделаем опыт с числом $\pi$‍,‍ аппроксимируя его разными долями — от первых до десятых. Вычисления опущены, читатель может воспроизвести их сам. $$ \def\mfrac#1#2{\dfrac{\enspace\mathclap{#1}\enspace}{\enspace\mathclap{#2}\enspace}} \def\d#1{\quad\mathllap{#1}} \def\f#1{0{,}\mathrlap{#1}\hphantom{0000}} \def\g#1#2{\quad\mathllap{#1}{,}\mathrlap{#2}\qquad} \colsep{4pt}{\begin{array}{c|c|c|c|c|c} \hline q&\colsep{0pt}{\footnotesize\begin{array}{c}\\[-5pt]\text{Прибли-}\\\text{жённое}\\\text{значение}\\\pi\\[-5pt]\\\end{array}}&\colsep{0pt}{\footnotesize\begin{array}{c}\text{Верхняя}\\\text{граница}\\\text{абсолютной}\\\text{погрешности}\end{array}}&\Delta&h&\lambda\quad\\ \hline &&&&&\\[-5pt] \d1&\mfrac31&\mfrac12=\f{5000}&\f{1416}&\f{1416}&\g35\\[12pt] \d2&\mfrac62&\mfrac14=\f{2500}&\f{1416}&\f{2832}&\g18\\[12pt] \d3&\mfrac93&\mfrac16=\f{1667}&\f{1416}&\f{4248}&\g12\\[12pt] \d4&\mfrac{13}4&\mfrac18=\f{1250}&\f{1084}&\f{4336}&\g12\\[12pt] \d5&\mfrac{16}5&\mfrac1{10}=\f{1000}&\f{0584}&\f{2920}&\g17\\[12pt] \d6&\mfrac{19}6&\mfrac1{12}=\f{0833}&\f{0251}&\f{1504}&\g33\\[12pt] \d7&\mfrac{22}7&\mfrac1{14}=\f{0714}&\f{0013}&\f{0089}&\g{56}{5~(!)}\\[12pt] \d8&\mfrac{25}8&\mfrac1{16}=\f{0625}&\f{0166}&\f{1327}&\g38\\[12pt] \d9&\mfrac{28}9&\mfrac1{18}=\f{0556}&\f{0305}&\f{2743}&\g18\\[12pt] \d{10}&\mfrac{31}{10}&\mfrac1{20}=\f{0500}&\f{0416}&\f{4159}&\g12\\[-5pt] &&&&&\\ \hline \end{array}} $$

Эта таблица показывает, что для аппроксимации $\pi$‍‍ седьмые доли резко выгоднее ближайших соседних долей. Фактическая погрешность в 56 раз меньше, чем можно думать, судя по размеру долей‍.

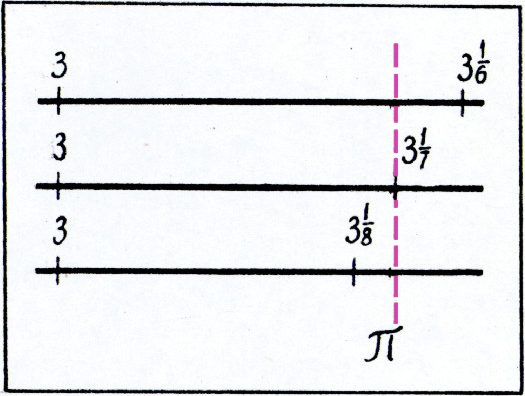
На рисунке 2 показано расположение числа $\pi$‍‍ на числовой оси. Случайно (а впрочем, случайно ли?) $\pi$‍‍ оказывается очень близко к $3\dfrac17$‍.‍ Если бы нам заранее предписали аппроксимировать так, чтобы абсолютная погрешность не превысила $0{,}0013$‍,‍ какие доли выбрали бы? Мы записали бы условие $\dfrac1{2q}\le 0{,}0013$‍,‍ откуда $q\ge385$‍,‍ а Архимед достиг той же точности, взяв гораздо меньший знаменатель.

Теперь вы убедились, читатель, что Архимед выбрал седьмые доли не случайно?

Через много веков голландский математик Адриан Меций дал приближённое значение $$ \pi\approx\dfrac{355}{113}. $$ Число Меция обладает теми же удивительными свойствами, что и число Архимеда: знаменатель 113 гораздо выгоднее, чем другие близлежащие знаменатели. Рекомендуем читателю исследовать число Меция так, как выше исследовано число Архимеда. Например, чему равен коэффициент выгодности?

2. Загадка Григория XIII. Григорий XIII не был математиком. Он был римским папой. Тем не менее его имя связано с важной математической задачей — с проблемой календаря.

Природа дала нам две естественные единицы времени: год и сутки (солнечные). Как сказано в одном старом учебнике космографии‍ «к сожалению, год не равен целому числу суток». С этим нельзя не согласиться, так как из упомянутого факта проистекает много неудобств. Зато он порождает интересную математическую проблему: $$ \text{1 год}=\text{365 суток 5 час. 48 мин. 46 сек.} $$ или $$ \text{1 год} = \text{365,242199 суток}. $$

Узаконить в гражданской жизни такую длину года невозможно. А что получится, если считать год равным 365 суткам? На рис. 3 показана орбита Земли. 1 января 1970 г. в 0 час. Земля находилась в точке $A$‍.‍ За 365 суток она не придёт в ту же точку орбиты и, следовательно, 1 января 1971 г. в 0 час. окажется в точке $B$‍,‍ а 1 января 1972 г. — в точке $C$‍‍ и т. д. Получится, что если фиксировать некоторую дату, то положение Земли на орбите будет каждый год иное (оно будет отставать почти на 6 часов).

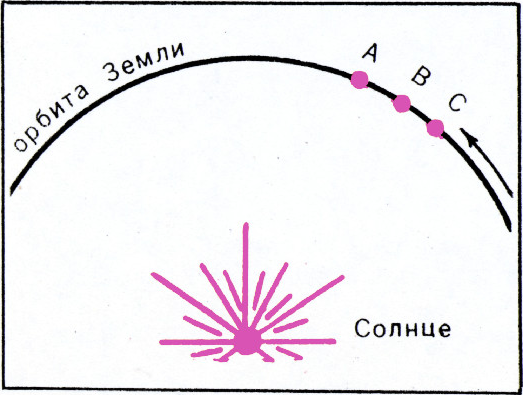
За четыре года отставание составит почти сутки, и фиксированная дата будет попадать на разные времена года, т. е. 1 января с зимы постепенно переместится на осень, потом на лето. Это неудобно: периодические мероприятия (посев, начало учебного года) нельзя будет связывать с определёнными календарными датами.

Выход из этого положения есть. Надо считать некоторые годы по 365 суток, а некоторые по 366 суток, чередуя их так, чтобы средняя длина года была возможно ближе к истинной. Можно воспроизвести истинную длину года с любой точностью, но для этого может понадобиться очень сложный закон чередования коротких (простых) и длинных (високосных) лет, что нежелательно. Нужен компромисс: сравнительно простой закон чередования лет, дающий среднюю длину года, достаточно близкую к истинной.

Эту задачу впервые разрешил Юлий Цезарь. Разумеется, к правителю слово «разрешил» может применяться лишь условно. Это сделал для него александрийский астроном Созиген, вызванный для этой цели в Рим. Юлий Цезарь ввёл такую систему: три года подряд коротких, четвёртый — длинный.

Много позже, когда было принято христианское летосчисление, високосными стали считать годы, номер которых делится на 4. Этот календарь называется «юлианским». По юлианскому календарю средняя длина года составляет $$ 365\dfrac14~\text{суток}=\text{365 суток 6 часов}.$$

Как видно, средняя длина юлианского года больше истинной на 11 мин. 14 сек. В 16 столетии папа Григорий XIII пожелал исправить эту неточность. В 1582 году он произвёл следующую реформу календаря. Сохраняется чередование простых и високосных лет, но оно дополняется правилом: если номер года оканчивается двумя нулями, а число сотен не делится на 4, то этот год простой. Например, по этому правилу 1700 год простой, но 1600 високосный.

Кроме того, считая, что от начала летосчисления (от «рождества Христова») уже накопилась ошибка в 10 дней, Григорий XIII сразу прибавил 10 дней. С тех пор накопилось ещё 3 дня (в 1700, 1800 и 1900 годах). Поэтому в настоящее время между юлианским календарём и новым («григорианским») расхождение составляет 13 дней.

Какова средняя длина григорианского года? Из 400 лет по юлианскому календарю 100 високосных, а по григорианскому — 97. Поэтому $$ \text{средняя длина григорианского года}= 365\dfrac{97}{400}~\text{суток}= 365{,}2425~\text{суток}= \text{365 суток 5 час. 49 мин. 12 сек.}, $$ т. е. она больше истинной на 26 сек.

Как видим, весьма простыми средствами достигнута очень большая точность.

В царской России до Великой Октябрьской революции пользовались юлианским календарём. Григорианский календарь был введён специальным декретом Совета Народных Комиссаров в 1918 году. Им мы и пользуемся в настоящее время. Степень его соответствия реальной длине солнечного года вполне достаточна для всех практических целей. Можно ли утверждать, что решение папы Григория XIII — самое простое и естественное? С ответом потерпите до конца этой статьи.

II. Цепные дроби

3. Понятие о цепной дроби. Забудем о десятичной системе счисления. Как говорил выдающийся русский математик Николай Николаевич Лузин (1883‍—‍1950), «преимущества десятичной системы не математические, а зоологические. Если бы у нас на руках было не десять пальцев, а восемь, то человечество пользовалось бы восьмеричной системой». Десятичная система практически очень удобна, но при исследовании теоретических вопросов арифметики она только мешает.

Итак, откажемся от специальных систем счисления, и задумаемся над вопросом: какой самый естественный способ приближённого представления положительных чисел дробями.

В ответе на этот вопрос не может быть никаких колебаний: надо прежде всего указать, между какими целыми числами оно заключено. Например, $$ \colsep{2pt}{ \begin{array}{cccccl} \dfrac{61}{27}&\text{находится}&\text{между}&2&\text{и}&3,\\[7pt] \sqrt2&\text{»}&\text{»}&1&\text{»}&2,\\ \pi&\text{»}&\text{»}&3&\text{»}&4. \end{array}} $$ Разумеется, достаточно указывать только меньшее из этих чисел: $$ \begin{alignat*}{3} \dfrac{61}{27}&=2+x&\quad(0\lt{}&x&{}\lt1),\\ \sqrt2&=1+y&\quad(0\lt{}&y&{}\lt1),\\ \pi&=3+z&\quad(0\lt{}&z&{}\lt1). \end{alignat*} $$ Заметим, что такая оценка не связана со способом обозначения целых чисел, т. е. с какой-нибудь конкретной системой счисления.

Займёмся числом $\dfrac{61}{27}$‍.‍ Наша оценка «два с лишним» слишком грубая и годится лишь как первое приближение. Если мы хотим сделать второй шаг, то мы должны оценить добавку $x$‍.‍ Поскольку она меньше единицы, естественно представить её как дробь с числителем 1 (мы опять апеллируем к «естественности», но это — в последний раз) $$ \dfrac{61}{27}=2+\dfrac1{x_1}. $$ Теперь $x_1$‍‍ больше единицы, и мы опять повторяем те же шаги: выделяем целую часть и т. д. и т. д. Приглашаем читателя внимательно проследить за чередованием этих двух шагов: $$ \begin{gather*} \dfrac{61}{27}=2+\dfrac7{27}=2+\dfrac1{\dfrac{27}7}=2+\dfrac1{3+\dfrac67}=\\ =2+\dfrac1{3+\dfrac1{\dfrac76}}=2+\dfrac1{3+\dfrac1{1+\dfrac16}}. \end{gather*} $$ Выражение $$ a_0+\dfrac1{a_1+\dfrac1{\begin{alignedat}{2} a_2+\vphantom{\dfrac11}\\[-5pt] &\ddots\\[-9pt] &&a_{s-1}+\dfrac1{a_s}\end{alignedat}}}, $$ где $a_1$‍,‍ $a_2$‍,‍ $\ldots$‍,‍ $a_s$‍‍ — натуральные числа, а $a_0$‍‍ — натуральное число или нуль, называется цепной дробью.

Числа $a_0$‍,‍ $a_1$‍,‍ $a_2$‍,‍ $\ldots$‍,‍ $a_s$‍‍ называются элементами‍ цепной дроби. Можно сказать, что мы представили число $\dfrac{61}{27}$‍‍ в виде цепной дроби.

Не слишком ли громоздко обозначение цепной дроби? В нашем примере получилась трёхэтажная дробь, а если получится двадцатиэтажная, то её нельзя уместить на листе бумаги.

Это верно, и поэтому для цепных дробей употребляются различные условные обозначения. Мы будем пользоваться таким: $$ a_0+\dfrac1{a_1+\dfrac1{ \begin{alignedat}{2} a_2+\vphantom{\dfrac11}\\[-5pt] &\ddots\\[-9pt] &&{}+\dfrac1{a_s} \end{alignedat} }}=[a_0;a_1,a_2,\ldots,a_s].\tag{*} $$ Обратите внимание на точку с запятой. Она подчёркивает, что роль целой части $a_0$‍‍ особая, не такая, как других чисел (особая — не значит более важная, в данном случае скорее наоборот).

Можно ли утверждать, что всякое действительное‍ число может быть изображено цепной дробью и притом единственным образом?

Прежде всего задумаемся над таким примером: $$ \dfrac1{6+\dfrac14}=\dfrac1{6+\dfrac1{3+1}}=\dfrac1{6+\dfrac1{3+\dfrac11}} $$ или в сокращённых обозначениях $$ [0;6,4]=[0; 6, 3, 1]. $$

Такое преобразование (отделение единицы от последнего элемента) можно произвести с любой цепной дробью, у которой последний элемент отличен от единицы. Если же последний элемент равен единице, то его можно прибавить к предпоследнему. Например, $$ [1;10,3,7,1]=[1;10,3,8]. $$ Легко, однако, доказать, что это — единственная причина неоднозначности представления рационального числа цепной дробью.

Можно доказать, что:

1) Процесс превращения рационального числа $\dfrac pq$‍‍ ($p$‍‍ и $q$‍‍ взаимно простые натуральные числа) в цепную дробь на некотором шаге заканчивается. Иначе говоря, любое положительное рациональное число представимо в виде $(*)$‍.‍ В силу только что сказанного такое представление всегда возможно и с соблюдением ограничения $a_s\gt1$‍.‍

2) Две цепные дроби $[a_0;a_1,\ldots,a_s]$‍‍ и $[b_0;b_1,\ldots,b_t]$‍,‍ у которых $a_s\gt1$‍‍ и $b_t\gt1$‍,‍ равны друг другу в том и только в том случае, если у них одинаковое число элементов, т. е. $s=t$‍‍ и $a_i=b_i$‍‍ при $i=1$‍,‍ 2, $\ldots$‍,‍ $s$‍.‍

Мы этого доказывать не будем. Цель нашей статьи в том, чтобы рассказать основные идеи и побудить читателя к более основательному изучению вопроса по книгам‍.

4. Бесконечные цепные дроби. А как быть с иррациональными числами? Попробуем разлагать в цепную дробь $\sqrt2 = 1{,}4142\ldots$‍.‍ Получим: $$ \begin{gather*} \sqrt2=1+\dfrac1{x_1},\\ x_1=\dfrac1{\sqrt2-1}=\sqrt2+1,\\ x_1=2+\dfrac1{x_2},\quad x_2=\sqrt2+1=x_1. \end{gather*} $$ Ясно, что $$ \begin{gather*} \sqrt2=1+\dfrac1x=1+\dfrac1{2+\dfrac1x}=1+\dfrac1{2+\dfrac1{2+\dfrac1x}}=\\ =1+\dfrac1{2+\dfrac1{2+\dfrac1{2+\dfrac1x}}}, \end{gather*} $$ где $x=\sqrt2+1$‍.‍

Хочется сразу написать $$ \sqrt2=1+\dfrac1{2+\dfrac1{2+\dfrac1{2+\dfrac1{2+\displaystyle{\vphantom{1}\atop\ddots}}}}}=[1;2,2,2,2,\ldots], $$ т. е. представить $\sqrt2$‍‍ в виде бесконечной цепной дроби. Но здесь нужна крайняя осторожность: мы встретились с новым понятием «бесконечная десятичная дробь», но не знаем, что? это такое. Легко понять только, что каждому положительному иррациональному числу соответствует вполне определённая бесконечная последовательность $$ [a_0;a_1,a_2,\ldots], $$ где $a_0$‍‍ — целое не отрицательное, а все $a_i$‍‍ с номером $i\ge1$‍‍ — натуральные числа. Во всём относящемся сюда мы разберёмся только позже‍, а пока удовлетворимся тем, что нам понятно: как по положительному числу $\alpha$‍‍ построить его формальное разложение $$ \alpha\sim[a_0;a_1,a_2,\ldots] $$ в конечную или бесконечную цепную дробь‍.

5. Подходящие дроби. Цепную дробь можно оборвать, удержав элементы $a_0$‍,‍ $a_1$‍,‍ $\ldots$‍,‍ $a_n$‍‍ и отбросив $a_{n+1}$‍,‍ $\ldots$‍‍ Полученное таким образом число называется $n$‍‍-й подходящей дробью и обозначается $\dfrac{p_n}{q_n}$‍.‍ В частности, при $n=0$‍‍ имеем нулевую подходящую дробь $\dfrac{p_0}{q_0}=\dfrac{a_0}1$‍.‍

Мы увидим, что, чем меньше $n$‍,‍ тем подходящая дробь проще (т. е. имеет меньший знаменатель). В то же время она может использоваться как приближённое значение цепной дроби.

Пример. Возьмём опять разложение числа $\dfrac{61}{27}$‍‍ в цепную дробь и образуем подходящие дроби $$ \begin{align*} \dfrac{p_0}{q_0}&=2,\\ \dfrac{p_1}{q_1}&=[2;3]=2+\dfrac13=\dfrac73,\\ \dfrac{p_2}{q_2}&=[2;3,1]=2+\dfrac1{3+\dfrac11}=\dfrac94,\\ \dfrac{p_3}{q_3}&=[2;3,1,6]=\dfrac{61}{27}. \end{align*} $$

Разумеется, последняя подходящая дробь рационального числа $\alpha$‍‍ равна $\alpha$‍.‍

Мы получили несколько постепенно усложняющихся приближений для числа $\dfrac{61}{27}$‍.‍ Для оценки их заметим, что $\dfrac{61}{27}\approx2{,}259$‍.‍ $$ \colsep{2pt}{ \begin{array}{lcll} \text{1-е}&\text{приближение}&2,&\quad\Delta=0{,}259.\\[3pt] \text{2-е}&\text{»}&\dfrac73=2{,}333,&\quad\Delta=-0{,}074.\\[9pt] \text{3-е}&\text{»}&\dfrac94=2{,}250,&\quad\Delta=0{,}009. \end{array}} $$

Мы замечаем, что погрешность убывает (по абсолютной величине) и имеет чередующиеся знаки. Это — общее правило.

В случае разложения в цепную дробь числа $\sqrt2=1{,}4142\ldots$‍‍ получим $$ \begin{array}{ll} \dfrac{p_0}{q_0}=1,&\Delta=0{,}4142,\\[9pt] \dfrac{p_1}{q_1}=[1;2]=\dfrac32=1{,}5,&\Delta=-0{,}0858,\\[9pt] \dfrac{p_2}{q_2}=[1;2,2]=\dfrac75=1{,}4,&\Delta=0{,}0142,\\[9pt] \dfrac{p_3}{q_3}=[1;2,2,2]=\dfrac{17}{12}=1{,}4167,&\Delta=-0{,}0025,\\[9pt] \dfrac{p_4}{q_4}=[1;2,2,2,2]=\dfrac{41}{29}=1{,}4138,&\Delta=0{,}0004. \end{array} $$ Мы наблюдаем и здесь ту же самую картину.

6. Основное свойство подходящих дробей. Сформулируем теперь без доказательства то основное свойство подходящих дробей, которое и приведёт к разгадкам наших загадок.

Если $\dfrac{p_n}{q_n}$‍‍ — подходящая дробь для числа $\alpha$‍,‍ то абсолютная погрешность $\left|\alpha-\dfrac{p_n}{q_n}\right|$‍‍ меньше, чем при аппроксимации числа $\alpha$‍‍ любой другой дробью с меньшим знаменателем‍.

Например, получив для $\sqrt2$‍‍ подходящую дробь $\dfrac{p_3}{q_3}$‍,‍ мы можем быть уверены, что приближение к $\sqrt2$‍‍ любой дроби со знаменателем, меньшим 12, будет хуже.

III. Разгадки

7. Загадка Архимеда. Попробуем разложить в цепную дробь число $\pi=3{,}14159265\ldots$‍:‍ $$ \pi=3+0{,}14159265\ldots=3+\dfrac1{7+0{,}00885145}. $$

Уже на этом этапе выкладок мы видим, что первыми подходящими дробями будут $$ \dfrac{p_0}{q_0}=3,\quad\dfrac{p_1}{q_1}=\dfrac{22}7. $$

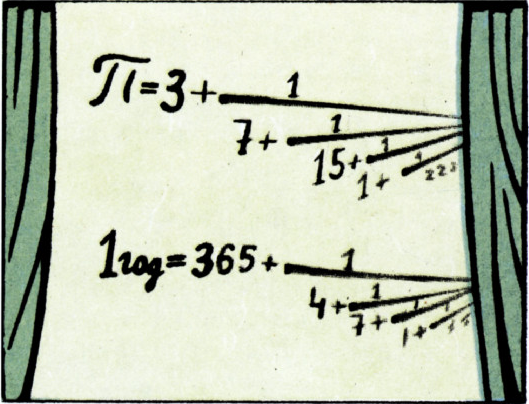
Проделайте сами выкладки и убедитесь, что $$ \begin{gather*} \pi\approx[3;7,15,1,288,1,\ldots],\\ \dfrac{p_2}{q_2}=\dfrac{333}{106},\quad \dfrac{p_3}{q_3}=\dfrac{355}{113}. \end{gather*} $$

Вот и всё. До чего же просто! Эта таблица раскрывает секрет Архимеда, а заодно и Меция. Из неё видно: $$ \colsep{2pt}{ \begin{array}{lcl} \text{1-е}&\text{приближение}&\pi\approx3,\\[3pt] \text{2-е}&\text{»}&\pi\approx\dfrac{22}7,\\[9pt] \text{3-е}&\text{»}&\pi\approx\dfrac{333}{106},\\[9pt] \text{4-е}&\text{»}&\pi\approx\dfrac{355}{113} \end{array}} $$ (нечётные приближения с недостатком, чётные — с избытком).

Можно ли считать, что Архимед и Меций разоблачены: они пользовались цепными дробями, Архимед использовал вторую подходящую дробь, а Меций — четвёртую?

Нет, про Архимеда этого сказать нельзя.

Следует ясно понять, что мы решили математическую, но не историческую задачу. Мы объяснили, как можно прийти к числу $\dfrac{22}7$‍.‍ Весьма возможно, что Архимед пользовался цепными дробями, но установить это по его работам нельзя. Суд не признал бы наших доводов. Историки не пришли к единому мнению. Преимущество седьмых долей можно обнаружить и эмпирически, сравнивая их с разными другими.

Другое дело Меций. Невероятно предположить, что такая сложная дробь как $\dfrac{355}{113}$‍,‍ найдена без теории. Очень вероятно, что Меций пользовался цепными дробями. Понятно почему он остановился на четвёртой подходящей дроби: следующие настолько громоздки, что практически непригодны.

8. Загадка Григория XIII. Сначала подумаем, как мы сами решили бы проблему чередования високосных лет. Мы представили бы длину года в виде цепной дроби: $$ \text{1 год}=365^{\text{д}}5^{\text{ч}}48^{\text{м}}46^{\text{с}}= 365{,}242199^{\text{д}}=[365;4,7,1,3,5,20,6,12]^{\text{д}}. $$

Примечание. $\pi$‍‍ — иррациональное число. Оно разлагается в бесконечную цепную дробь. Величина года — эмпирическая. Всякая эмпирическая величина измеряется лишь с определённой точностью, и говорить об её рациональности или иррациональности не имеет смысла. Приведённая выше величина года — принятая, и мы должны считать её точной. Она выражается конечной цепной дробью.

Находим несколько первых подходящих дробей: $$ \begin{align*} \dfrac{p_0}{q_0}&=365,\\ \dfrac{p_1}{q_1}&=365+\dfrac14=365\dfrac14,\\ \dfrac{p_2}{q_2}&=365+\dfrac1{4+\dfrac17}=365\dfrac7{29},\\ \dfrac{p_3}{q_3}&=365+\dfrac1{4+\dfrac1{7+\dfrac11}}=365\dfrac8{33},\\ \dfrac{p_4}{q_4}&=365+\dfrac1{4+\dfrac1{7+\dfrac1{1+\dfrac13}}}=365\dfrac{31}{128}. \end{align*} $$ Каждая подходящая дробь даёт решение проблемы календаря. Например, приближение $365\dfrac14$‍‍ приводит к решению Юлия Цезаря: один високосный год из каждых четырёх. Пользоваться приближением $365\dfrac7{29}$‍‍ никто не предлагал, по-видимому, потому, что следующее приближение $365\dfrac8{33}$‍‍ лишь немного сложнее, но значительно точнее. Календарь, по которому високосными должны были бы считаться восемь лет из каждых тридцати трёх, был предложен великим туркмено-персидским философом, математиком, астрономом и поэтом Омаром Хайямом (1040‍—‍1123).

Сведения о точности найденных приближений к истинной длине года даны в следующей таблице. $$ \begin{array}{c|c|c|c} \hline\\[-7pt] \colsep{0pt}{\footnotesize\begin{array}{c} \text{№ при-}\\\text{ближе-}\\\text{ния}\end{array}}& \footnotesize\text{Чередование високосных лет}& \footnotesize\text{Средняя длина года}& \footnotesize\text{Погрешность}\\[-7pt]\\\hline\\[-5pt] \colsep{0pt}{\begin{array}{c}1\\2\\3\\4\end{array}}& \colsep{2pt}{\begin{array}{rcccr} 1&\text{високосн.}&\text{из}&\text{каждых}&4\\ 7&\text{»}&\text{»}&\text{»}&29\\ 8&\text{»}&\text{»}&\text{»}&33\\ 31&\text{»}&\text{»}&\text{»}&128\end{array}}& \colsep{2pt}{\begin{array}{rrrr} 365^{\text{д}}&6^{\text{ч}}&00^{\text{м}}&00^{\text{с}}\\ 365^{\text{д}}&5^{\text{ч}}&47^{\text{м}}&35^{\text{с}}\\ 365^{\text{д}}&5^{\text{ч}}&49^{\text{м}}&05^{\text{с}}\\ 365^{\text{д}}&5^{\text{ч}}&48^{\text{м}}&45^{\text{с}}\end{array}}& \colsep{0pt}{\begin{array}{crr} {-}&11^{\text{м}}&~14^{\text{с}}\\ {+}&1^{\text{м}}&11^{\text{с}}\\ &&\mathllap{-}19^{\text{с}}\\ &&\mathllap{+}\hphantom91^{\text{с}}\end{array}} \\[-5pt]\\\hline \end{array} $$

В графе «Погрешность» знак минус указывает, что средняя длина года больше истинной.

Четвёртый вариант исключительно точен. Погрешность в 1 сек. не имеет никакого практического значения. Поэтому были предложения использовать этот календарь. Например, в 1864 году русский астроном Медлер предложил с Х столетия ввести такой календарь в России. Для этого надо внести в юлианский календарь следующую поправку: каждые 128 лет пропускать один високосный (потому что по юлианскому календарю на 128 лет приходится 32 високосных). Однако этот календарь не был принят нигде в мире, по-видимому, потому, что период 128 «некруглый».

Решив математическую задачу, вернёмся к задаче исторической. Каковы были соображения Григория XIII (или его сотрудников)?

В начале статьи говорилось, что средняя длина григорианского года 365 суток 5 час. 49 мин. 12 сек. Это значение отличается от истинного на целых 26 секунд. Получается впечатление, что папа Григорий XIII или его учёные советники придумали календарь более сложный, чем хайямовский и к тому же менее точный. Значит ли это, что они были плохими математиками? Оказывается дело не в этом.

При Григории XIII продолжительность года не была известна столь точно, как теперь. Комиссия Григория XIII пользовалась астрономическими таблицами, составленными Альфонсом Х (1221‍—‍1284), королём Кастилии, который занимался астрономией (недаром его прозвали Альфонс-астроном). Эти таблицы впервые были изданы в Венеции через сто лет после смерти их автора. В них даётся следующая продолжительность года: $$ \text{1 год}=365^{\text{д}}~5^{\text{ч}}~49^{\text{м}}~16^{\text{с}}. $$

Пользуясь этими таблицами, комиссия должна была прийти к выводу, что предложенная ею средняя длина календарного года только на четыре секунды отличается от истинной. Если бы комиссия и была знакома с предложением Омара Хайяма, то она пришла бы к выводу, что его календарь даёт ошибку в 11 секунд.

Добавим, что нет никаких оснований предполагать, что комиссия Григория XIII использовала цепные дроби. Она кропотливо, в поте лица подбирала нужное соотношение.

Что касается Омара Хайяма, то учёные думают, что он владел, если не полной теорией цепных дробей, то каким-либо аналогичным принципиальным подходом к задачам о наиболее рациональных приближениях дробями с небольшими знаменателями. В его эпоху восточная наука во многих отношениях стояла выше европейской.

Задачи

1. Найдите коэффициент выгодности для числа Меция.
2. Разложите в цепную дробь $\dfrac{157}{225}$‍.‍
3. Сверните цепную дробь $[3;12,2,1,50]$‍.‍
4. Разложите в цепную дробь $$ \text{а) }\sqrt3;\quad \text{б) }\sqrt5;\quad \text{в) }\sqrt6. $$ Попробуйте самостоятельно (ещё не обращаясь к книжкам) подумать о свойствах цепных дробей, которые получаются при разложении $\sqrt n$‍,‍ где $n$‍‍ — натуральное число, не являющееся квадратом натурального числа.
5. Найдите значения периодических цепных дробей а) $[0;a,a,a,\ldots]$‍;‍ б) $[0;a,b,a,b,\ldots]$‍.‍

6. Некоторые восточные народы пользуются смешанным солнечно-лунным календарём. Месяцы у них имеют то 29, то 30 дней. Месяцы из 29 дней называются «пустыми», а из 30 дней «полными». Календарный год состоит то из двенадцати, то из тринадцати месяцев. Греческий математик Метон (433 год до нашей эры) предложил замечательное решение проблемы лунно-солнечного календаря. По Метону из каждых 19 лет семь имеют по тринадцать месяцев, а остальные двенадцать лет — по двенадцать месяцев. Из общего числа 235 лунных месяцев, помещающихся в «золотом» девятнадцатилетнем периоде, 110 пустых и 125 полных. Здесь люди столкнулись с более сложной задачей одновременного приближения к отношениям трёх величин — длины суток, длины лунного месяца и длины солнечного года. С достаточно хорошим приближением $$ \begin{gather*} \text{1 солнечный год}=\text{365,2422 суток},\\ \text{1 лунный месяц}=\text{29,5306 суток}. \end{gather*} $$ Наши задачи будут относиться лишь к отношениям каждой пары из этих величин в отдельности. Отношением длины года к длине суток мы уже занимались. Теперь разложите в цепную дробь отношение $\dfrac{\text{1 солнечный год}}{\text{1 лунный месяц}}$‍.‍ Вы получите объяснение удачи изобретения Метона.

   Разложите в цепную дробь и отношение длины лунного месяца к суткам.