Изображения страниц
Текст статьи Гик Е. Я. Теорема Пифагора на шахматной доске // Квант. — 1975. — № 9. — С. 23.
На шахматной доске нарисуем квадрат, как показано на рисунке 1. Доска разбивается на этот квадрат и четыре конгруэнтных прямоугольных треугольника. Теперь посмотрим на рисунок 2. На нём мы видим те же четыре треугольника, что и на рисунке 1. Значит, треугольники на обоих рисунках занимают одну и ту же площадь. Следовательно, одну и ту же площадь в обоих случаях занимают и оставшиеся части шахматной доски без треугольников. Итак, площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна площади двух квадратов, построенных на катетах, — «пифагоровы штаны во все стороны равны»!
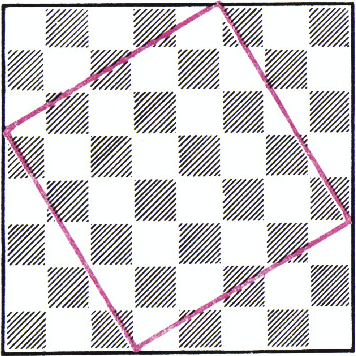

Может быть, гроссмейстер М. Таль имел в виду именно это доказательство теоремы Пифагора.
(Разумеется, если говорить строго, наши рассуждения не доказывают теорему Пифагора, поскольку исследован лишь некоторый частный случай, а лишь иллюстрируют её. Но такое доказательство проходит и без использования шахматной доски — для любого прямоугольного треугольника можно подобрать квадрат, который разбивается подобным образом.)
